针对多密度数据的密度峰值聚类算法改进毕业论文【附代码+数据】

原创于 2024-10-24 13:38:19 发布 · 622 阅读

6 ·

CC 4.0 BY-SA版权

文章标签：

#1024程序员节

✅ 博主简介：擅长数据处理、建模仿真、程序设计、仿真代码、论文写作与指导，毕业论文、期刊论文经验交流。

✅ 具体问题可以私信或扫描文章底部二维码。

（1）多密度数据划分与参数d_c的自适应选择

在原始的密度峰值聚类（DPC）算法中，参数d_c（截断距离）的选择是至关重要的，它直接影响每个数据点的局部密度计算以及聚类中心的选择。然而，对于多密度数据集，单一参数d_c难以满足不同密度区域的需求，导致聚类效果不佳。为了解决这一问题，本文引入了K近邻思想，通过计算每个数据点的K近邻距离，实现了数据集的自适应划分。

具体而言，我们首先计算数据集中每个数据点的K近邻距离，即该数据点到其第K近邻的距离。然后，将这些距离按升序排列并绘制成k近邻距离折线图。在折线图中，全局分叉点（即斜率发生显著变化的点）被用来作为划分不同密度区域的依据。全局分叉点的选择基于一种启发式方法，即寻找折线图中斜率变化最大的点。一旦找到全局分叉点，我们将数据集划分为两部分：高密度区域和低密度区域。对于高密度区域，我们选择较小的d_c值以捕捉更精细的聚类结构；而对于低密度区域，我们选择较大的d_c值以覆盖更广泛的邻域。

这种方法的有效性在于，它允许算法根据数据的局部密度特性自动调整参数d_c，从而克服了原始DPC算法在处理多密度数据时的局限性。

（2）聚类中心的自动选择与优化

在DPC算法中，聚类中心的选择通常依赖于决策图（即局部密度与距离乘积的散点图）上的主观判断。然而，这种方法不仅缺乏客观性，还可能引入误差。为了解决这个问题，本文提出了一种新的聚类中心选择方法，该方法结合了局部密度、距离以及γ高度差的概念，实现了聚类中心的自动确定。

首先，我们计算每个数据划分中每个数据点的局部密度和距离，并绘制γ图。γ图上的每个点表示一个数据点，其横坐标为局部密度，纵坐标为距离。然后，我们计算γ图上所有点之间的高度差，并求出高度差的平均值。这个平均值反映了γ图上点的分布特征，即聚类中心与非聚类中心之间的差异程度。

接下来，我们进行两次筛选：第一次筛选是基于高度差阈值的，即选择高度差大于平均值一定倍数的点作为候选聚类中心；第二次筛选是基于最大间断点的，即在候选聚类中心中，找到局部密度最大且与前一个候选聚类中心距离最远的点作为最终的聚类中心。同时，我们通过计算候选聚类中心的数量来确定聚类中心的个数。

这种方法不仅提高了聚类中心选择的客观性，还减少了人为误差的引入。此外，通过自适应地选择聚类中心，算法能够更好地适应不同密度数据集的聚类需求。

（3）聚类结果的融合与算法应用

在得到每个数据划分中的聚类结果后，我们需要将这些结果进行融合，以形成最终的聚类结果。为了实现这一目标，本文提出了一种基于簇间相似度的融合规则。具体而言，我们首先计算每个簇的质心，并根据质心之间的距离来判断簇之间的相似度。然后，我们设置一个相似度阈值，将相似度高于阈值的簇进行合并。通过这种方式，我们可以有效地整合不同数据划分中的聚类结果，形成更加准确和完整的聚类结构。

为了验证改进算法（F-DPC）的有效性和优越性，我们在多种人工模拟数据集和UCI真实数据集上进行了实验。实验结果表明，F-DPC算法在聚类效果、聚类质量、样本数量等方面均优于原始的DPC算法和其他经典聚类算法。此外，我们还将F-DPC算法应用于新闻文本聚类中，通过预处理文本数据、提取特征向量、构建相似度矩阵等步骤，成功地将新闻文本聚类为不同的主题类别。这一应用不仅展示了F-DPC算法在文本聚类领域的潜力，还证明了其在实际问题中的有效性和实用性。

% data = load('your_data.mat'); % 示例：加载数据文件  
  
% 参数设置  
K = 10; % K近邻参数  
threshold_height_diff = 1.5; % 高度差阈值  
similarity_threshold = 0.5; % 簇间相似度阈值  
  
% 计算K近邻距离  
k_distances = pdist2(data, data, 'euclidean');  
[~, sorted_indices] = sort(k_distances, 2);  
k_neighbor_distances = k_distances(sub2ind(size(k_distances), repmat((1:size(data,1)),1,K), sorted_indices(:,K)));  
  
% 绘制k近邻距离折线图并找到全局分叉点  
figure;  
plot(k_neighbor_distances, 'b-');  
hold on;  
[~, idx_fork] = findpeaks(-diff(k_neighbor_distances), 'MinPeakHeight', 0, 'MinPeakDistance', 10);  
fork_point = k_neighbor_distances(idx_fork + 1); % 全局分叉点  
  
% 根据全局分叉点划分数据集并计算局部密度和距离  
data_high_density = data(k_neighbor_distances <= fork_point, :);  
data_low_density = data(k_neighbor_distances > fork_point, :);  
  
% 为高密度区域和低密度区域分别设置d_c值  
d_c_high = median(pdist2(data_high_density, data_high_density, 'euclidean')) * 0.5;  
d_c_low = median(pdist2(data_low_density, data_low_density, 'euclidean')) * 1.5;  
  
% 计算局部密度和距离（以高密度区域为例）  
distances_high = pdist2(data_high_density, data_high_density, 'euclidean');  
densities_high = sum(distances_high < d_c_high, 2);  
gamma_high = densities_high .* max(distances_high, [], 2);  
  
% 绘制γ图并找到候选聚类中心  
figure;  
scatter(densities_high, max(distances_high, [], 2), 'filled');  
hold on;  
avg_height_diff = mean(diff(sort(gamma_high(end:-1:1))));  
candidate_centers_idx = find(diff(sort(gamma_high(end:-1:1))) > avg_height_diff * threshold_height_diff);  
candidate_centers_idx = flipud(candidate_centers_idx); % 恢复原始顺序  
  
% 选择最终聚类中心（最大间断点）  
final_centers_idx = [];  
for i = 1:length(candidate_centers_idx)  
    if isempty(final_centers_idx) || max(pdist2(data_high_density(final_centers_idx, :), data_high_density(candidate_centers_idx(i), :), 'euclidean')) > d_c_high  
        final_centers_idx = [final_centers_idx, candidate_centers_idx(i)];  
    end  
end  
  
% 对低密度区域进行类似处理（省略具体代码）  
% ...  
  
% 聚类结果融合（示例：仅融合高密度区域和低密度区域的聚类结果）  
% 假设已经分别得到高密度区域和低密度区域的聚类标签labels_high和labels_low  
% 将低密度区域的聚类结果加上一个偏移量以避免标签冲突  
offset = max(labels_high) + 1;  
labels_low = labels_low + offset;  
  
% 合并数据集和标签  
combined_data = [data_high_density; data_low_density];  
combined_labels = [labels_high; labels_low];  
  
% 计算簇间相似度并融合簇  
% 省略具体代码，基于质心和相似度阈值进行融合  
% ...  
  
% 显示聚类结果  
figure;  
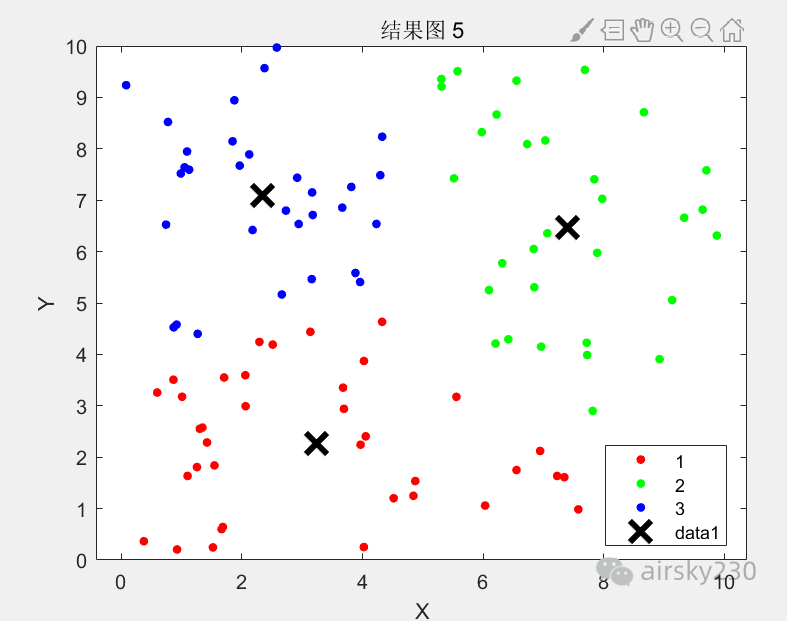
gscatter(combined_data(:,1), combined_data(:,2), combined_labels);  
title('F-DPC算法聚类结果');  
xlabel('特征1');  
ylabel('特征2');