中考python编程题样题,中考信息技术python

大家好，小编来为大家解答以下问题，中考python编程题样题，中考信息技术python，今天让我们一起来看看吧！

题目：辽宁沈阳2020中考数学第25题(压轴)

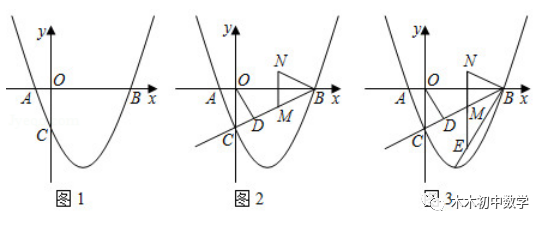
25．如图1，在平面直角坐标系中，O是坐标原点，抛物线y＝x2/2+bx+c经过点B(6，0)和点C(0，﹣3)．

(1)求抛物线的表达式；

(2)如图2，线段OC绕原点O逆时针旋转30°得到线段OD．过点B作射线BD，点M是射线BD上一点(不与点B重合)，点M关于x轴的对称点为点N，连接NM，NB．

①直接写出△MBN的形状为   ；

②设△MBN的面积为S1，△ODB的面积为是S2．当S1＝2S2/3时，求点M的坐标；

(3)如图3，在(2)的结论下，过点B作BE⊥BN，交NM的延长线于点E，线段BE绕点B逆时针旋转，旋转角为α(0°＜α＜120°)得到线段BF，过点F作FK∥x轴，交射线BE于点K，∠KBF的角平分线和∠KFB的角平分线相交于点G，当BG＝2根号3时，请直接写出点G的坐标为   ．

问(1)b=-5/2，c=-3；y＝x2/2-5x/2-3；顶点(5/2，-49/8)，A(-1,0)

问(2)①等边三角形；

②M(3，-根号3)；

①由线段OC绕原点O逆时针旋转30°得到线段OD，D(3/2，-3根号3/2);

直线BD:y=根号3x/3-2根号3(x≤6)。特殊斜率，∠OBM=30°，对称性可知,∠NBO=30°，NB=MB，∠NBM=60°，△MBN是等边三角形神码ai智能写作介绍。

②∠DOB=60°，∠OBD=30°，则∠ODB=90°，OB=6，S2=9根号3/2

正三角形的面积公式，同学们最好记住S=根号3*a^2/4，a是正三角形的边长。

设M的坐标(m,根号3m/3-2根号3),m＜6.

正三角形的高：6-m，则边长可求，面积可求，代入S1＝2S2/3

解出m=3或者m=9(舍)，M(3，-根号3)

(3)NB⊥BE，则∠OBE=60°，直线BE的表达式可求：y=根号3x-6根号3；

E(3，-3根号3)，EB=6.

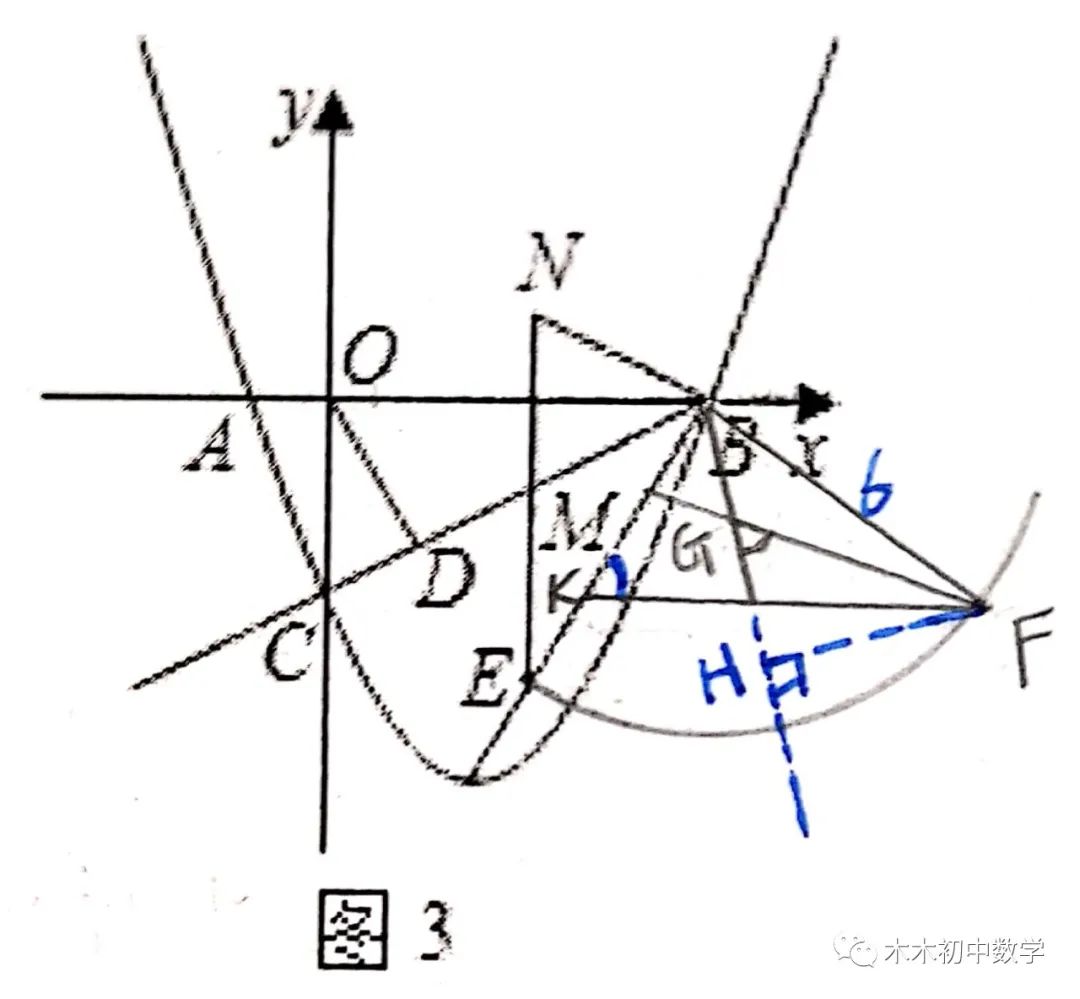
∵FK∥x轴，∠OBE=60°

∴∠BKF=60°，G是角分线交点，未分前两角和是120°，则∠HGF=60°(特殊角)

BF=BE=6,BG=2根号3，过点F作BG的垂线交其延长线于点H。

设GH=a，则HF=根号3a，在直角△BHF中，使用勾股定理，a=根号3；

BH=3根号3，HF=3，而BF=6,∴∠HBF=30°，△EBF是正三角形。

G是正三角形的中心。

∠KBG=30°，BG∥y轴。

B(6，-2根号3)

最后一问，在基本分析完成后，角分线上的BG怎么使用是个问题。此时BF已知，∠HGF=60°，在这种情况下，就可以构造直角三角形。实在做不出的时候，可以尝试特殊角度，也就是正三角形，发现刚好能得正解，哈哈。