第37-38天学习笔记——位运算

• 位运算
  • 异或运算：^ 相同为0，不同为1
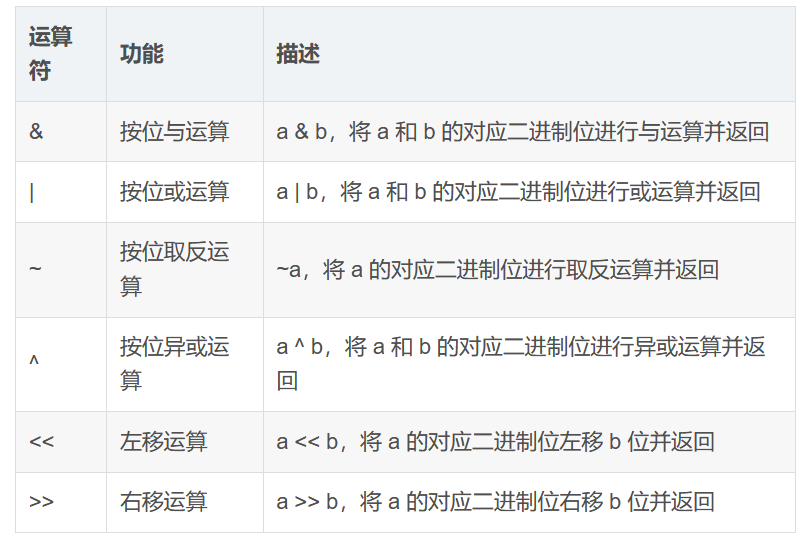
  • 几种常用运算符

    

  • 不需要额外空间的方法，就往位运算上想
  • 假设 a = 1, b = 0
  • 1、 1 ⊕ 0 = 1, 0 ⊕ 0 = 0 => a ⊕ 0 = 1, b ⊕ 0 = 0 ==> 任何数与0做异或运算结果均为其本身
  • 2、 1 ⊕ 1 = 0, 0 ⊕ 0 = 0 => a ⊕ a = 0, b ⊕ b = 0 ==> 任何数与其本身做异或运算结果均为0
  • 3、 1 ⊕ 0 ⊕ 1 = 0 => 1 ⊕ 1 = 0 => a ⊕ b ⊕ a = b
  • 1 ⊕ 1 ⊕ 0 = 0 => 0 ⊕ 0 = 0 => a ⊕ a ⊕ b = b
  • 0 ⊕ (1 ⊕ 1) = 0 => 0 ⊕ 0 = 0 => b ⊕ (a ⊕ a) = b
  • ==>异或运算满足交换律和结合律
  • LeetCode 136、只出现一次的数字
    • 为了满足 算法应该具有线性时间复杂度与不使用额外空间来实现，本题通过寻找位运算规律来解决。
    • 由于 非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次， 即数组中元素数量恒为奇数。
    • 假设数组中有 2n + 1 个元素，有 n 个元素为出现两次的元素，如果所有数进行连续异或操作可得：
    • A1 ⊕ A1 ⊕ A2 ⊕ A2 ...... ⊕ An ⊕ An ⊕ An+1= (A1 ⊕ A1) ⊕ (A2 ⊕ A2) ...... ⊕ (An ⊕ An) ⊕ An+1 //通过规律3= (0) ⊕ (0) ...... ⊕ (0) ⊕ An+1 //通过规律2= An+1 //通过规律1
    • 通过规律1可知，我们在做连续异或操作的时候，可以以0为起始数开始运算。
    • 这道题就是让每一位数字做异或运算，结果就是只出现一次的数字
  • LeetCode 137、只出现一次的数字 II
    • 因为出现三次的元素，它的0对结果没有贡献（三个0相加还是0），它的1对结果有贡献，因为三个1相加为3，所以对结果的每一位相加除以3，相当于把三个的元素除外了，再取余就得到了最终只出现一次的元素
    • 转换为二进制，然后按位运算，把每一位都累加，然后模3操作，模3的余数就是只出现一次的那个数字
    • 注意以下的这个操作：先移位，再与1进行按位与操作，即可得到每个位置1的个数
    • for j in range(32) :
      • temp = num >> j
      • x = temp & 1
  • LeetCode 260、只出现一次的数字 III（需要熟练掌握这道题目的思想，面试重点）
    • 解题思路： 算法要求时间复杂度是O(N)，时间复杂度是O(1) 所以不可以通过暴力解法来解决该题
    • 简单来说就是通过先通过异或操作得到sum，再找到sum中为1的那个位（根据两个数异或，不同为1，相同为0），也就是找到了将数组分成a,b两组的那个位，然后再通过相与操作分成两组，再分别异或即可找到a和b
    • 1、由于 nums 中其余元素均出现两次
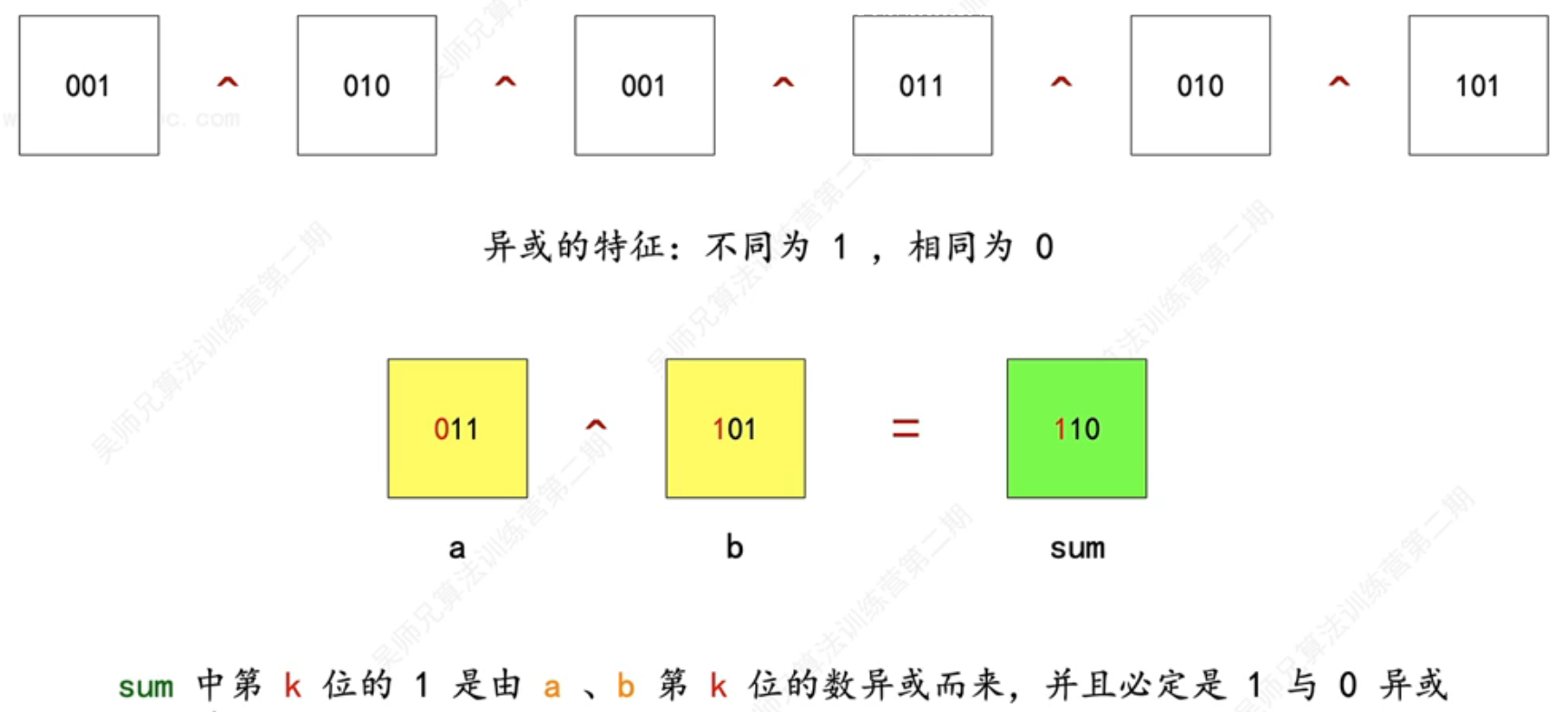
    • 2、异或的特征：不同为 1 ，相同为 0
    • 因此，最终的 sum 就是那两个只出现一次的元素异或的结果
    • 假设这两个只出现一次的元素分别为 a 和 b
    • a = 011 , b = 101 , 那么 sum = 110
    • 也就意味着 sum 上面的 1 必然是由 a 与 b 贡献的，因为两个相同元素的二进制必然相同，异或一下为 0
    • 假设 sum 上面的第 k 位是 1
    • 那么，我们可以将 nums 划分为两部分数组
      • 1、第 k 位是 1，包含了 b 与 nums 中第 k 位是 1 的元素，并且这些元素出现了两次
      • 2、第 k 位是 0，包含了 a 与 nums 中第 k 位是 0 的元素，并且这些元素出现了两次
    • 也就是说，a 与 b 划分到了不同的部分
    • 而相同的元素进行异或为 0 ，那么每一部分进行异或最终就剩下了一个只出现一次的元素

    • 

    • "sum & (-sum)" 操作的结果就是原始数值 "sum" 的最低非零位的二进制位。
    • 另外，这种操作在编程中有时用于快速确定一个整数是否为2的幂，因为只有2的幂的二进制表示中只有一个 1，其余位都为 0，所以 "sum & (-sum)" 结果为非零表示 "sum" 是2的幂，否则不是。
  • LeetCode 641、 汉明距离
    • 先异或得到不同位，然后将结果右移0到32位后与1进行相与操作，如果为1则让计数+=1即可