大学学习数据结构的时候做过一个计算算术表达式字符串结果的小程序,最近学习java接触到了类似的问题,不过不是计算结果,而是利用它来构造二叉树,难度稍微大了一些。我在这里提供两种解决方案。相信很多人都知道怎么计算表达式的值,利用两个栈(符号栈和数字栈)根据运算符优先级进行出栈入栈操作,我们知道将栈中的运算符和数字替换为二叉树的节点就可以在这个过程中顺利的构造一个二叉树出来。第二种方法利用了递归的思想,我们构造二叉树的难点其实主要在于括号的存在,假设一个没有括号的算数表达式,如1+2*3-8/4,我们取得第一个运算符+的时候,将其作为一个树节点,将1和2分别作为左孩子和右孩子;当我们取得*时,将2和3分别作为它的左右孩子,由于*优先于+,所以*将成为+的右孩子;当我们取得-时,将3和8作为其左右孩子,由于-优先级低于*,所以要往上找*的父亲+,由于-的优先级低于+,所以继续找+的父亲,由于+已经没有父亲,+将成为-的孩子;最后取得/时,由于/优先级高于-,所以直接作为-的右孩子。个人感觉这两种方法都比较好理解。第二种方法的二叉树构造顺序如下(直线上的数字代表构造的次序,比较有趣的是用第一种方法和第二种方法构造出来的二叉树好像是一样的):
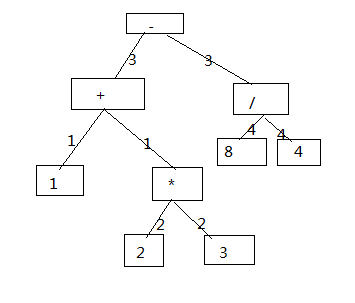
其中用到了基本的数据结构树节点TreeNode<E>,使用时应该用TreeNode<Character>,特别注意第一种方法不要求树节点中保存父指针,但第二种要求要保留父指针。两种方法的核心代码列在下面了:
第一种:
/**
* 将part解析为二叉树
* @param part
* @return 返回二叉树的根节点,解析失败返回null
*/
public TreeNode<Character> createBinaryTree(String part){
//定义数字栈和操作符栈
Stack<TreeNode<Character>> numStack=new Stack<TreeNode<Character>>();
Stack<TreeNode<Character>> operStack=new Stack<TreeNode<Character>>();
operStack.push(new TreeNode<Character>('#',null,null,null));
for(int i=0;i<part.length();i++){
//是数字则直接压入数字栈
if(isNumber(part.charAt(i))){
numStack.push(new TreeNode<Character>(part.charAt(i),null,
null,null));
continue;
}
//是操作符(注意这里没有把左右括号当做操作符)或者左括号,则尝试压入
//符号栈
if(isOperator(part.charAt(i))||part.charAt(i)=='('){
Character top=operStack.get(operStack.size()-1).getData();
//如果准备压入的符号比栈顶端的符号优先级低,则栈顶段的符号
//和数字栈中的数字应该弹出,两个数字是符号节点的左右孩子,
//再将符号节点压入数字栈(此时该符号节点已经代表一个数字了,
//所以要压入数字栈)
while(getPriority(top, part.charAt(i))<0){
//如果符号栈只剩下#,说明算术表达式已经解析完了,返
//回数字栈中的节点
if(top=='#'){
return numStack.pop();
}
TreeNode<Character> temp=operStack.pop();
TreeNode<Character> right=numStack.pop();
TreeNode<Character> left=numStack.pop();
temp.setLefChild(left);
temp.setRigChild(right);
numStack.push(temp);
top=operStack.get(operStack.size()-1).getData();
}
operStack.push(new TreeNode<Character>(part.charAt(i),null,null,null));
continue;
}
//如果将入栈的是右括号,则符号栈弹出符号并和数字栈弹出的数字组建树节
//点,知道碰到左括号。
if(part.charAt(i)==')'){
Character top=operStack.get(operStack.size()-1).getData();
while(top!='('){
TreeNode<Character> temp=operStack.pop();
TreeNode<Character> right=numStack.pop();
TreeNode<Character> left=numStack.pop();
temp.setLefChild(left);
temp.setRigChild(right);
numStack.push(temp);
top=operStack.get(operStack.size()-1).getData();
}
operStack.pop();
continue;
}
}
return null;
}
第二种方法:/**
* 利用算数字符串content构造二叉树binaryTree
*/
public TreeNode<Character> CreateBinaryTree(String part){
//先将表达式转换为由不含括号的节点组成的链表结构
List<TreeNode<Character>> list=new ArrayList<TreeNode<Character>>();
for(int i=0;i<part.length();i++){
if(isNumber(part.charAt(i)) || isOperator(part.charAt(i))){
list.add(new TreeNode<Character>(part.charAt(i),null,null,
null));
}else {
//如果不是操作数和操作符,那肯定是括号,如果表达式正确,
//第一碰到的括号肯定是左括号
int right=findFitBracket(part, i);
String subPart=new String(part.substring(i+1, right));
list.add(CreateBinaryTree(subPart));
i=right;
}
}
//根据这个不含括号的链表结构构造二叉树
TreeNode<Character> cur=null;
for(int i=0;i<list.size();i++){
if(isOperator(list.get(i).getData()) && list.get(i).getLefChild()
==null){
list.get(i).setLefChild(list.get(i-1));
list.get(i).setRigChild(list.get(i+1));
list.get(i-1).setFather(list.get(i));
list.get(i+1).setFather(list.get(i));
if(cur==null)
cur=list.get(i);
else {
while(priority(cur.getData(),list.get(i).getData())<0
&& cur.getFather()!=null)
cur=cur.getFather();
if(cur.getFather()==null &&
priority(cur.getData(),
list.get(i).getData())<0){
list.get(i).setLefChild(cur);
cur.setFather(list.get(i));
}
else {
if(priority(cur.getData(),
list.get(i).getData())>0){
cur.setRigChild(list.get(i));
list.get(i).setFather(cur);
}
}
}
cur=list.get(i);
}
}
while(cur.getFather()!=null)
cur=cur.getFather();
return cur;
}






















 2360
2360

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








