[LC] 311. Sparse Matrix Multiplication

最新推荐文章于 2024-03-24 10:28:52 发布

原创最新推荐文章于 2024-03-24 10:28:52 发布 · 194 阅读

0 ·

CC 4.0 BY-SA版权

Leetcode 专栏收录该内容

294 篇文章

订阅专栏

博客围绕稀疏矩阵乘法展开，指出正常矩阵运算对左、右矩阵维度有要求，给出常规二维矩阵乘法代码，该代码未针对稀疏特点优化。通过调整三个for - loop的顺序，让continue语句发挥作用，可利用稀疏特征跳过内层循环，实现代码优化。

https://leetcode.com/problems/sparse-matrix-multiplication/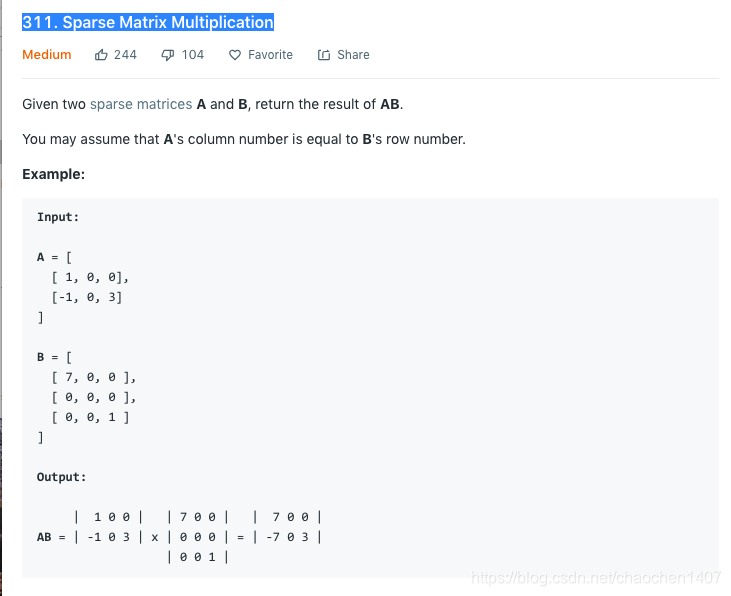

正常的矩阵运算要求左矩阵的长和右矩阵的高是一样的。也就是A[0].length == B.length。然后结果数组的size就是result[B[0].length][A.length]。具体怎么算还是随便google一下吧

如果按照正常算二维矩阵的代码，最后是这个样子的。

    public int[][] multiply(int[][] A, int[][] B) {
        int[][] result = new int[A.length][B[0].length];
        
        for (int i = 0; i < A.length; i++) {
            for (int j = 0 ; j < B[0].length; j++) {
                for (int k = 0; k < A[0].length; k++) {
                    result[i][j] += A[i][k] * B[k][j];
                }
            }
        }
        
        return result;
    }

这样写的话，是最正常的计算矩阵乘法的流程。但是对sparse这个特点并没有任何优化。

我先给一段很蠢的代码

        for (int i = 0; i < A.length; i++) {
            for (int j = 0 ; j < B[0].length; j++) {
                for (int k = 0; k < A[0].length; k++) {
                    if (A[i][k] == 0 || B[k][j] == 0) continue;
                    result[i][j] += A[i][k] * B[k][j];
                }
            }
        }

在这里，这个continue其实基本上没有做任何优化。但是这个新加的一行代码其实就是关键所在。我们仔细阅读一下原来的代码，会发现三个for-loop的顺序不管怎么变换，都不会改变运算的结果。也就是譬如说下面这样也是对的

    public int[][] multiply(int[][] A, int[][] B) {
        int[][] result = new int[A.length][B[0].length];
        
        for (int i = 0; i < A.length; i++) {
            for (int k = 0; k < A[0].length; k++) {
                for (int j = 0 ; j < B[0].length; j++) {
                    result[i][j] += A[i][k] * B[k][j];
                }
            }
        }
        
        return result;
    }

在这里，我把k和j换了一个位置，但是并不会改变最后算出来的结果。同样你换一下i和k的位置也是一样的。这样做的意义是在于，让上面我写的那个continue，变得有意义了。如果在源代码里面，把j和k的位置换一下，就像上面那样，那么那个continue的位置，也可以挪到第二层的for-loop里而不是最里面那层。同样，这样就可以利用到sparse这个特征，跳过很多个最里面那层的for-loop。所以最后的代码就是

    public int[][] multiply(int[][] A, int[][] B) {
        int[][] result = new int[A.length][B[0].length];
        
        for (int i = 0; i < A.length; i++) {
            for (int k = 0; k < A[0].length; k++) {
                if (A[i][k] == 0) continue;
                for (int j = 0 ; j < B[0].length; j++) {
                    result[i][j] += A[i][k] * B[k][j];
                }
            }
        }
        
        return result;
    }