数据结构（上）--选择排序，插入排序，希尔排序，冒泡排序思想及代码实现

选择排序

思想：遍历n次，每次将该位置的数与其后的数比较，找到最小的数并与之交换

时间复杂度：O(N^2)
空间复杂度：O(1)
稳定性：不稳定
画图文字表述过程：这时最简单的排序方式，也是最麻烦的方式

应用场景：列表基本有序时，需要寻找最小值时  

void SelectSort(int *arr, int len)//选择法排序，每次与元素后面的数字排序
{
	int tmp = 0;
	for (int i = 0; i < len - 1; i++)
	{
		for (int j = i + 1; j < len; j++)
		{
			if (arr[i] > arr[j])
			{

				tmp = arr[i];
				arr[i] = arr[j];
				arr[j] = tmp;
			}
		}
	}
}

 

插入排序

思想：每次从无序表中取出第一个元素，把它插入到有序表的合适位置，使有序表仍然有序

时间复杂度：O(N^2)

空间复杂度：O(1)

稳定性：稳定

过程：

1.像揭扑克牌一样，第一张8不动

 

2.第二张4插在8前面，第三张9本就在8后，故不动

 

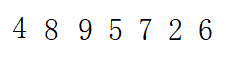
3.第四张5插到4后

4.第五张7插在8前一个位置

5.第六张2插在最前面

6.最后一张6插在七前面

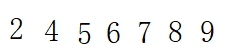
应用场景：适用于排序小列表，若列表基本有序，则插入排序比冒泡、选择更有效率

void InsertSort(int *arr, int len)  //插入排序
{
	int i;//趟数
	int tmp;
	int j;
	for (i = 1; i < len; i++)
	{
		tmp = arr[i];
		for (j = i - 1; j >= 0; j--)
		{
			if (arr[j] > tmp)
			{
				arr[j + 1] = arr[j];
			}
			else
			{
				break;
			}
		}
		arr[j + 1] = tmp;
	}
}

冒泡排序

思想：比较相邻的二个数据，并合理交换，这样对数组的第0个数据到N-1个数据进行一次遍历后，最大的一个数据就“沉”到数组第N-1个位置。重新令N=N-1，重复前面二步直到N变为0

时间复杂度：O(N^2)       空间复杂度：O(1)
稳定性：稳定
算法优化：

 

1. 记住最后一次交换发生的位置，此位置之后肯定是有序的，无需再比较
2. 当数列本就有序时，循环N-1次太过浪费，这时需要一个flag来判断一趟冒泡完后是否有数值交换，没有交换则说明有序，直接return
   画图文字表述过程：

                    

所以结果是：0 2 4 5 8 9

应用场景：列表基本有序时

void BubbleSort(int *arr, int len)  //冒泡排序
{
	int tmp;
	bool swap = false;
	for (int i = 0; i < len - 1; i++)
	{
		bool swap = false;
		for (int j = 0; j < len - 1 - i; j++)
		{
			if (arr[j] > arr[j + 1])
			{
				tmp = arr[j];
				arr[j] = arr[j + 1];
				arr[j + 1] = tmp;
				bool swap = true;
			}
			if (!swap)
			{
				return;
			}
		}
	}
}

 

希尔排序

思想：先取一个小于n的整数d1作为第一个增量，把文件的全部记录分组。所有距离为d1的倍数的记录放在同一个组中。先在各组内进行直接插入排序；然后，取第二个增量d2<d1重复上述的分组和排序，直至所取的增量dt=1，即所有记录放在同一组中进行直接插入排序为止

时间复杂度：O（NlogN）~ O（N^1.5）
空间复杂度：O(1)
稳定性：不稳定
过程：一般的初次取序列的一半为增量，以后每次减半，直到增量为1。子序列不是逐段分割的，而是相隔特定的增量的子序列，对各个子序列进行插入排序；然后再选择一个更小的增量，再将数组分割为更多个子序列进行排序......     比较相隔较远距离（称为增量）的数，使得数移动时能跨过多个元素，则进行一次比较就可能消除多个元素交换

1.将这组数据分成六小组（len/2=6）

2.将每组数据进行直接插入排序

3.将整组数据重新分成三组（6/2）

4.将每组数据进行直接插入排序

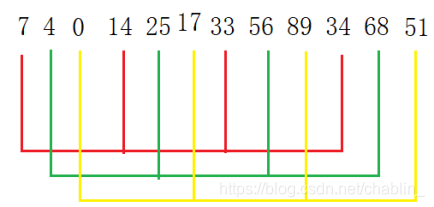
5.将整组数据重新分成一组（3/2），并进行插入排序

应用场景：中等规模下表现好，它好在最坏情况和平均情况差不多，快排最坏情况效率很低

void shell(int *arr, int len, int gap)//希尔排序
{
	int tmp = 0;
	int j = 0;
	for (int i = gap; i < len; i++)
	{
		tmp = arr[i];
		for (j = i - gap; j >= 0; j = j - gap)
		{
			if (arr[j] >tmp)
			{
				arr[j + gap] = arr[j];
			}
			else
			{
				break;
			}
		}
		arr[j + gap] = tmp;
	}
}
void shellSort(int *arr, int len)//希尔排序
{
	int drr[] = { 5,3,1 };
	int lend = sizeof(drr) / sizeof(drr[0]);
	for (int i = 0; i < lend; i++)
	{
		shell(arr, len, drr[i]);
	}
}