树叉和树（上）

集合是否相交：例如以下非树

 

树的性质或者依据：

1.子树不相交

2.除了根结点外，每个结点仅有一个父结点；（一个儿一个爹）

3.一棵N个结点的树N-1条边

树的一些术语：

1.度--（子）树

2.叶结点：度为0

3.结点的度，树的度，父结点，子结点，兄弟结点，路径和路径长度，祖先结点，子孙结点，结点的层次，树的深度都很好理解

二叉树的定义

有穷结点集合

可以为空，也可以由根节点和（左子树和右子树）组成

 

 

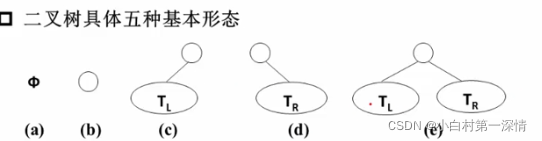
特殊二叉树：

斜二叉树和完美（满）二叉树

 

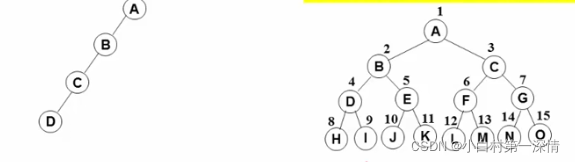
完全二叉树

有n个结点的一义树，对树甲结点按 从上至下、从左到右顺序进行编号， 编号为i(1≤i≤n)结点与满二叉树 中编号为ⅰ结点在二叉树中位置相同

例如：

 

 

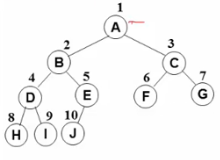
以上是

以下却不是

 

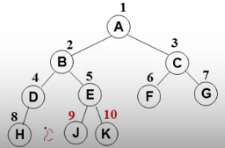
很多数据结构就建立在这种树上

二叉树几个重要性质：

1 一个二叉树第i层的最大结点数为：21，i≥1。

2 深度为k的二叉树有最大结点总数为：2k1,k≥1。 1+2+2 3 对任何非空二叉树T,若n,表示叶结点的个数、n2是 度为2的非叶结点个数，那么两者满足关系no=n2+1。

操作集

：BT∈BinTree,ltem∈ElementType,重要操作有： 1、Boolean IsEmpty(BinTree BT):判别BT是否为空； 2、void Traversal(BinTree BT):遍历，按某顺序访问每个结点； 3、BinTree CreatBinTree():创建一个二叉树。

常用的遍历方法有： ◆void PreOrderTraversal(BinTree BT):先序--根、左子树、右子树： ◆void InOrderTraversal(BinTree BT):中序-左子树、根、右子树： ◆void PostOrderTraversal(BinTree BT):后序--左子树、右子树、根 ◆void LevelOrderTraversal(BinTree BT):层次遍历，从上到下、从左到右

二叉树的存储结构

1.顺序存储结构

完全二叉树：从上到下，从左到右顺序存储n结点的完全二叉树的结点父子关系

 

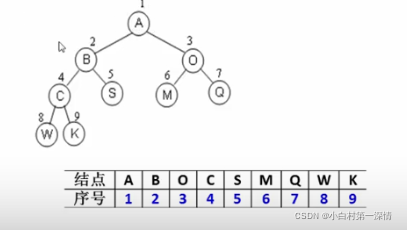
特点：已知其中任何一个结点都能推断出他的子父结点

非根结点（序号i>1)的父结点的序号是Li/2]
    结点（序号为ⅰ）的左孩子结点的序号是2

(若2i<=n,否则没有左孩子)； 结点（序号为ⅰ）的右孩子结点的序号是2i+1, (若2i+1<=n,否则没有右孩子)；

思考

 

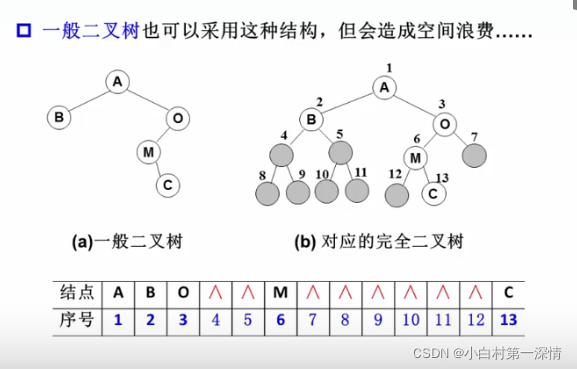
2.链表存储

常用来存储一般的二叉树

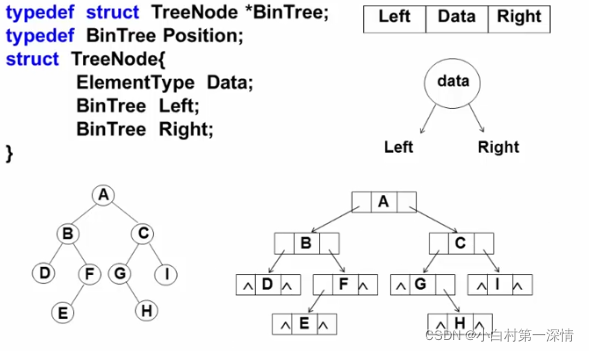
二叉树的遍历

四种遍历：先序遍历，中序遍历，后序遍历，

(1)先序遍历 遍历过程为： ①访问根节点 ②先序遍历其左子树： ③先序遍历其右子树。

 

 

(2)中序遍历 遍历过程为：

中序遍历其左子树；

访问根结点；

中序遍历其右子树。

 

 

 

 

(3)后序遍历 遍历过程为： 后序遍历其左子树：

后序遍历其右子树：

访问根结点。

 

 

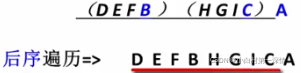
总结

先序、中序和后序遍历过程：遍历过程中经过结点的路线一 样，只是访问各结点的时机不同。

在递归的基础上，递归用堆栈，借助堆栈将递归转换为非递归

 

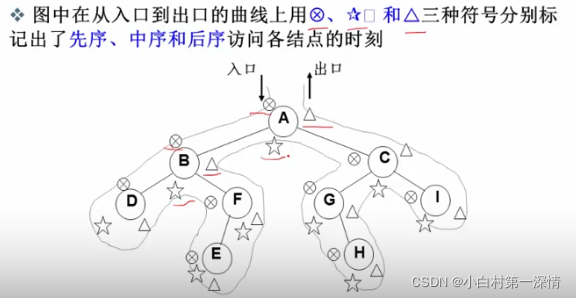
二叉树的非递归遍历

中序遍历非递归遍历算法 非递归算法实现的基本思路：使用堆栈（待补充，练习堆栈）

 

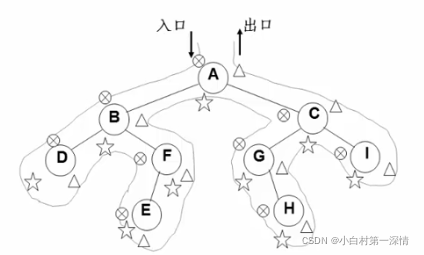
遇到一个结点，就把它压栈，并去遍历它的左子树： 当左子树遍历结束后，从栈顶弹出这个结点并访问它： )然后按其右指针再去中序遍历该结点的右子树。

 

先序遍历的非递归遍历算法

 

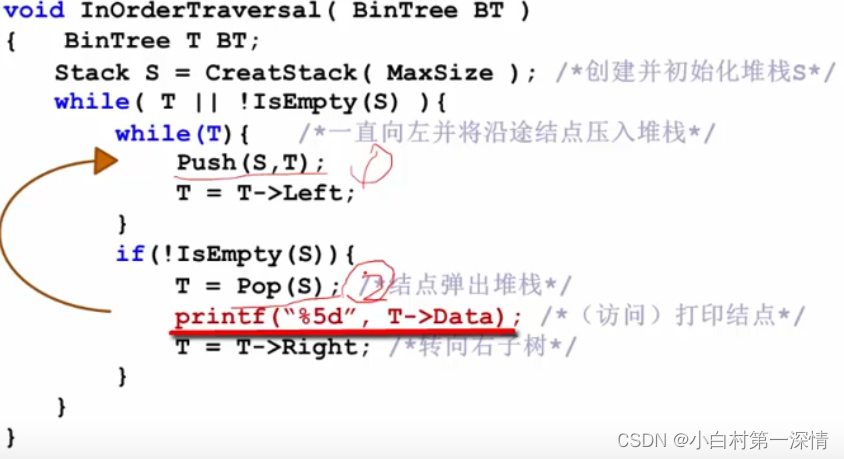
请思考后序遍历，如何形成非递归算法？