
欢迎来到Cefler的博客😁
🕌博客主页:那个传说中的man的主页
🏠个人专栏:题目解析
🌎推荐文章:题目大解析(3)

前言
宏观看待递归的过程
1.不要在意递归的细节展开图
2.把递归的函数当成一个黑盒
3.相信这个黑盒一定能完成这个任务
如何写好一个递归?
1.先找到相同的子问题->函数头的设计
2.只关心某一个子问题是如何解决的->函数体的书写
3.注意一下递归函数的出口即可
递归的本质就是对一棵树进行深度优先遍历(层序遍历)
👉🏻汉诺塔
原题链接:汉诺塔问题
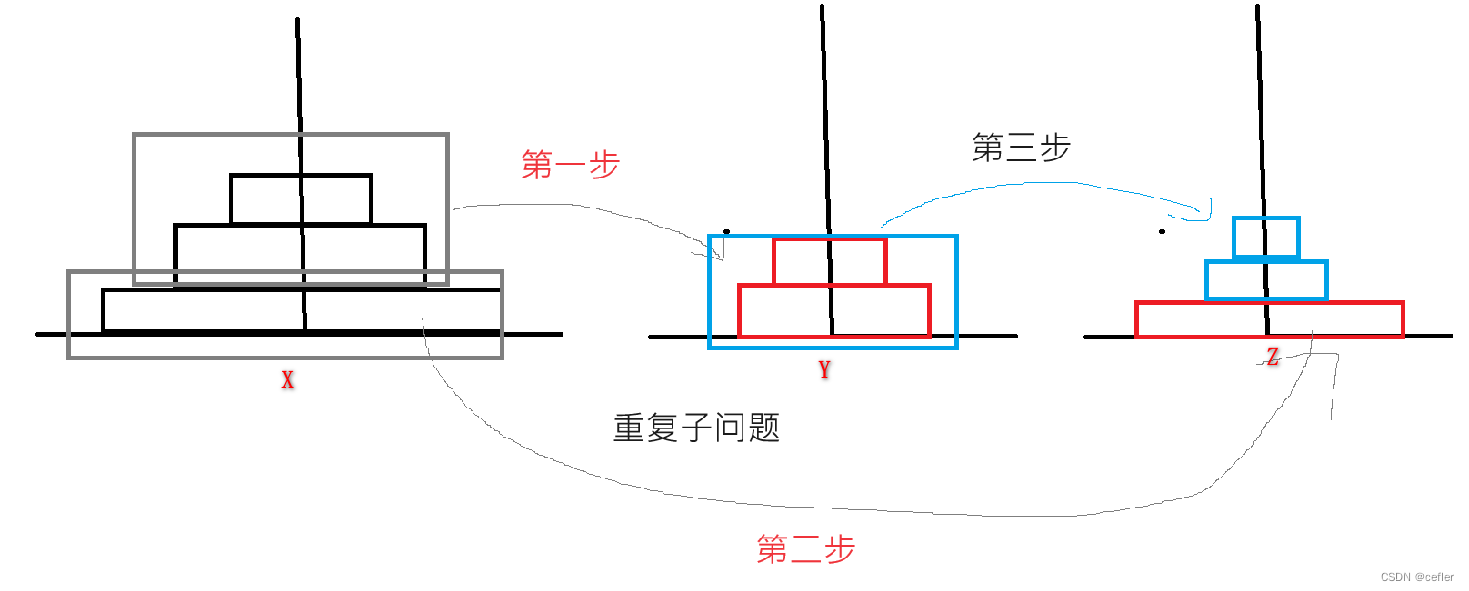
mycode:
class Solution {
public:
void difs(vector<int>& x, vector<int>& y, vector<int>& z,int n)
{
if(n==1)
{
z.push_back(x.back());
x.pop_back();//记得将原柱子的盘子删除
}
else
{
difs(x,z,y,n-1);//x借助z柱将n-1个盘子挪动到y柱上
z.push_back(x.back());//此时将底部盘子挪动到z柱子上
x.pop_back();
difs(y,x,z,n-1);//再将y柱上n-1个盘子借助x柱挪动到z上
}
}
void hanota(vector<int>& a, vector<int>& b, vector<int>& c) {
int n = a.size();
difs(a,b,c,n);
}
};
👉🏻合并两个有序链表
原题链接:合并两个有序链表
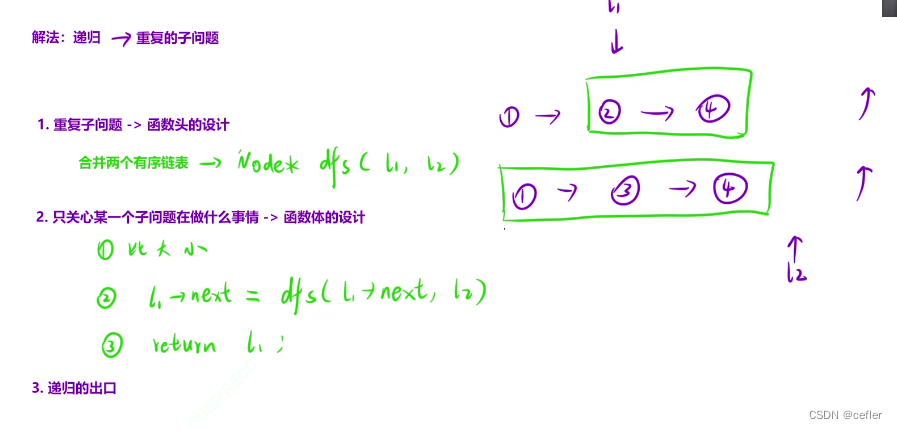
mycode:
class Solution {
public:
ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
if(list1==nullptr||list2==nullptr)
{
if(list1==nullptr)
return list2;
else
return list1;
}
else
{
if(list1->val<list2->val)
{
list1->next = mergeTwoLists(list1->next,list2);
return list1;
}
else
{
list2->next = mergeTwoLists(list1,list2->next);
return list2;
}
}
}
};
👉🏻矩形切割
小明有一些矩形的材料,他要从这些矩形材料中切割出一些正方形。
当他面对一块矩形材料时,他总是从中间切割一刀,切出一块最大的正方形,剩下一块矩形,然后再
切割剩下的矩形材料,直到全部切为正方形为止。
例如,对于一块两边分别为 5 和 3 的材料(记为 5×3),小明会依次切出 3×3、2×2、1×1、1
×1 共 4 个正方形。
现在小明有一块矩形的材料,两边长分别是 2019 和 324。请问小明最终会切出多少个正方
mycode:
#include<iostream>
using namespace std;
int dif(int l, int w)
{
if (l == w)
return 1;
else
{
//谁长减谁
if (l > w)
{
return dif(l - w, w) + 1;
}
else
return dif(l, w - l) + 1;
}
}
int main()
{
int l, w;
cin >> l >> w;
int ret = dif(l, w);
cout << ret << endl;
return 0;
}
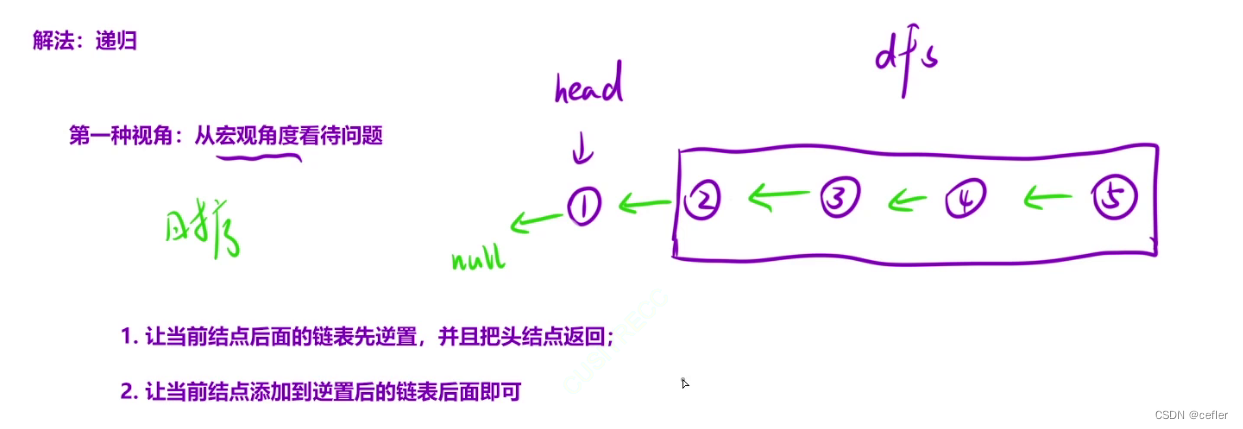
👉🏻反转链表
原题链接:反转链表
mycode:
class Solution {
public:
// ListNode* reverse(ListNode* head)
// {
// }
ListNode* reverseList(ListNode* head) {
if(head == nullptr||head->next==nullptr)
return head;
else
{
ListNode* newHead = reverseList(head->next);//先dif遍历到最后一个节点
//此时reverseList已经帮我们把head之后的所有节点都完成了逆序工作,我们只需要做最后的收尾工作
head->next->next = head;
head->next = nullptr;
return newHead;
}
}
};
👉🏻Pow(x, n)
原题链接:Pow(x, n)
mycode:
class Solution {
public:
double myPow(double x, int n) {
return n<0?1.0/pow(x,-(long long)n):pow(x,n);
}
double pow(double x , int n){
if(n==0) return 1.0;
double tmp = pow(x ,n/2);
return n%2==0?tmp*tmp:tmp*tmp*x;
}
};

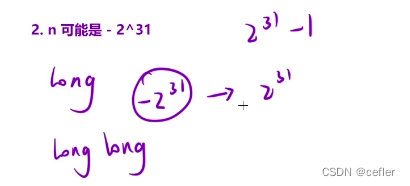






 本文介绍了递归的基本概念,通过实例演示了汉诺塔问题、合并有序链表、矩形切割、反转链表以及Pow(x,n)的解决方案,展示了如何通过递归实现深度优先遍历。
本文介绍了递归的基本概念,通过实例演示了汉诺塔问题、合并有序链表、矩形切割、反转链表以及Pow(x,n)的解决方案,展示了如何通过递归实现深度优先遍历。
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








