红黑树初识

搜索是十分重要的

比如我们去搜索信息，用谷歌，百度或者youtube什么的

顺序搜索（sequential search）

顺序搜索顾名思义，也就是根据顺序比对元素进行搜索。比如我们又一个数组：

[8,3,10,1,6,4,7,13]

比如我们去搜索4
那就需要顺序比对，也就是先比较8，3, 10，1，6，然后才能比较到4
但是如果我们去搜索5
同样需要顺序比对，而且是从8一路比对到13，但是最后的结果肯定是搜索不到因为数组里面没有5
所以这种搜索的效率肯定是很低下的，也就是说它的时间复杂度是O(n)

二分查找（binary search）

对于二分查找来说我们这时假设需要查找的数组中的元素是有序的，亦或是说查找数组的元素属性的关键字是有序的。这时候数组如下：

[1,3,4,6,7,8,10,13]

这时候再去搜索4，那比较顺序是先和数组中间的元素去比较，也就是去和6比较，发现比6要小就往左边走去和左边中间的数做比较，也就是再去和3比较，和3比较完毕后发现4比3大，所以再去右边比较也就是3的右边是4那么就找到我们想要的结果了。那么对于元素5的查找也是一样的，按照4的方法来

所以二分查找是非常快的，因为对于二分查找来说，它的时间复杂度是O(log2n)，也就是说如果我们又1024个元素，用二分查找只需要比对10次就可以找到，但是对于顺序查找可能就要比较1024次，那么几万个元素呢，几十万个呢，亿级元素呢。

顺序序列暴露问题

[1,3,4,6,7,8,10,13]

对于效率如此之高的二分查找，首先要保证序列有序，既然有序，那么插入删除元素的工作量就会加大，就比如我们插入一个5，我们肯定不能插在开头或者结尾，因为这样整个序列就变成无序的了，也就没有什么意义了。所以我们为了保证整个序列的有序性，保证二分查找的可行性。所以我们要去寻找正确的元素位置，但是这时候5后面的元素就都要后移，那么如果一共的元素总个数有亿级级别，那就要后移大量的元素，如果是删除则要前移大量的元素，所以开销是十分巨大的。那么在这种条件下，缺点就日益暴露了出来。

二叉查找树（binary search tree BST）

二叉查找树是可以和二分法查找一样的，也就是相较于二分查找效率是一样的。
并且对于插入删除也不再需要移动大量的元素。基本形态如下

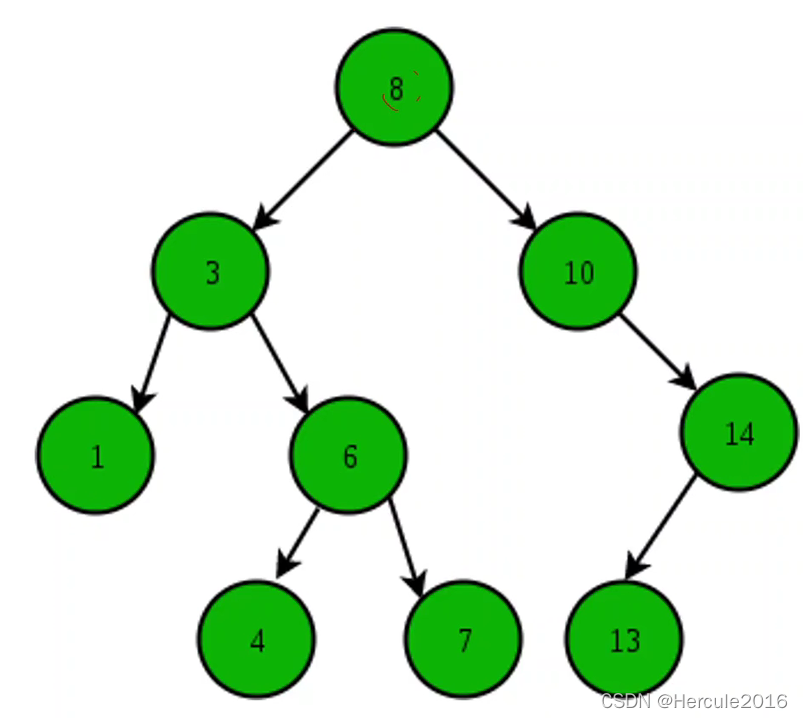
对于二叉查找树其左子树是比父节点要小的，而右子树都要大于父节点，所有节点满足一个次序。
所以对于此种数据结构，和二分法的查找也是一样的，比如查找元素4，先和8比较既然比8要小所以 再去左孩子找再和3比较比3要大再和3的右孩子比较也就是和6比较发现比6小那么就再和6的左孩子比较，也就是和4比较，这时候元素就找到了。

所以对于二叉查找树来说，搜索过程是从根走到叶子，那么对于二叉查找树来说其时间复杂度为O(h)。也就是说查找的次数要走一个树的高度。但是这种树也分不同的情况有可能树是平衡的，也有可能是不平衡的那就存在两种极端的情况：
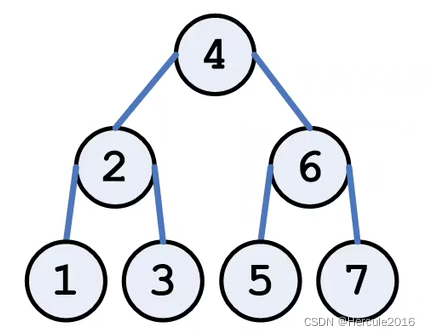
一种是平衡的：

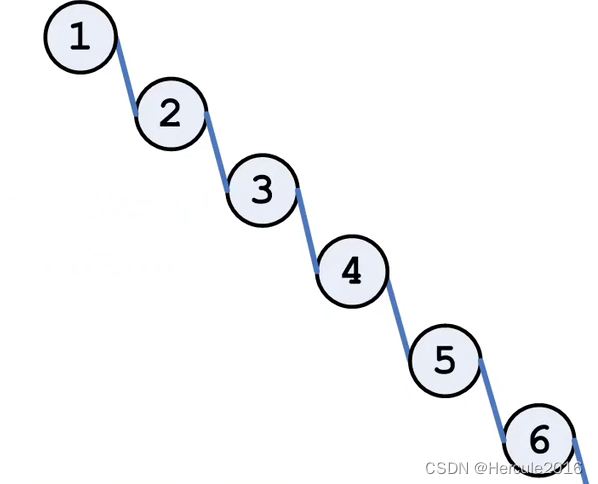
另一种是不平衡的：

那么这个时候就会出现两种极端的状况
那么对于绝对平衡的二叉查找树树的高度就是h = [log2n] + 1，ASL = [log2n]+1
不平衡的二叉树就不是很幸运了，极不平衡的二叉树就会变成上面那种h= n的情况，这时候查询效率会下降到ASL=(n+1)/2,也就是基本退化到线性序列的，所以此时的二叉查找树也就没有任何的意义。

平衡二叉树（AVL tree）

平衡二叉树的出现也就是为了改进原本的二叉树的不平衡的问题，因为一旦树变的不平衡就很有可能退化为顺序表，这时候我们肯定是需要最平衡的二叉树来保证查找效率。
对于平衡二叉树其概念是任何一个节点，左子树的节点和右子树的节点之差不超过1，那么我们就称其为平衡二叉树。所以我们就称其为平衡二叉树或者AVL树。
公式为：|Height(RightTree)|-Height(LeftTree)| <=1

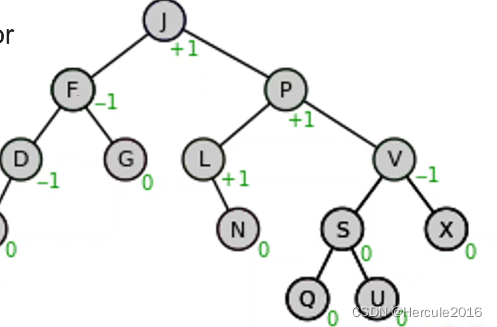
也就是说平衡二叉树基本长上面那个样子
所以对于AVL树其高度也就是 h = [log2n]+1,所有可以看到二叉平衡树的查找效率非常高，也不会出现不平衡的问题了。但是其插入或者删除算法就会变得很复杂了，因为本来树是平衡的，你删除一个节点，或者插入一个节点就有可能导致树的不平衡，所以就要做出调整了。

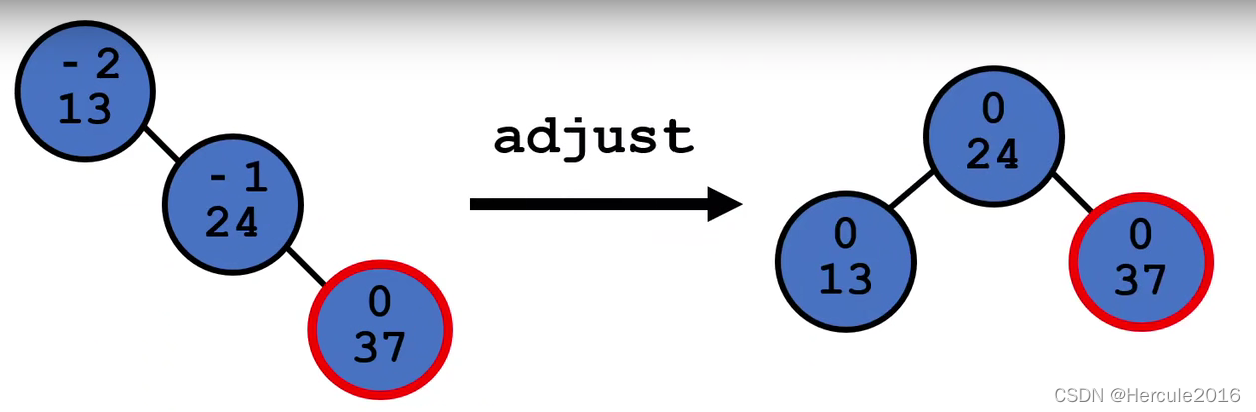
这时候需要对树做出调整，就将节点向左旋转，称为节点的左旋。
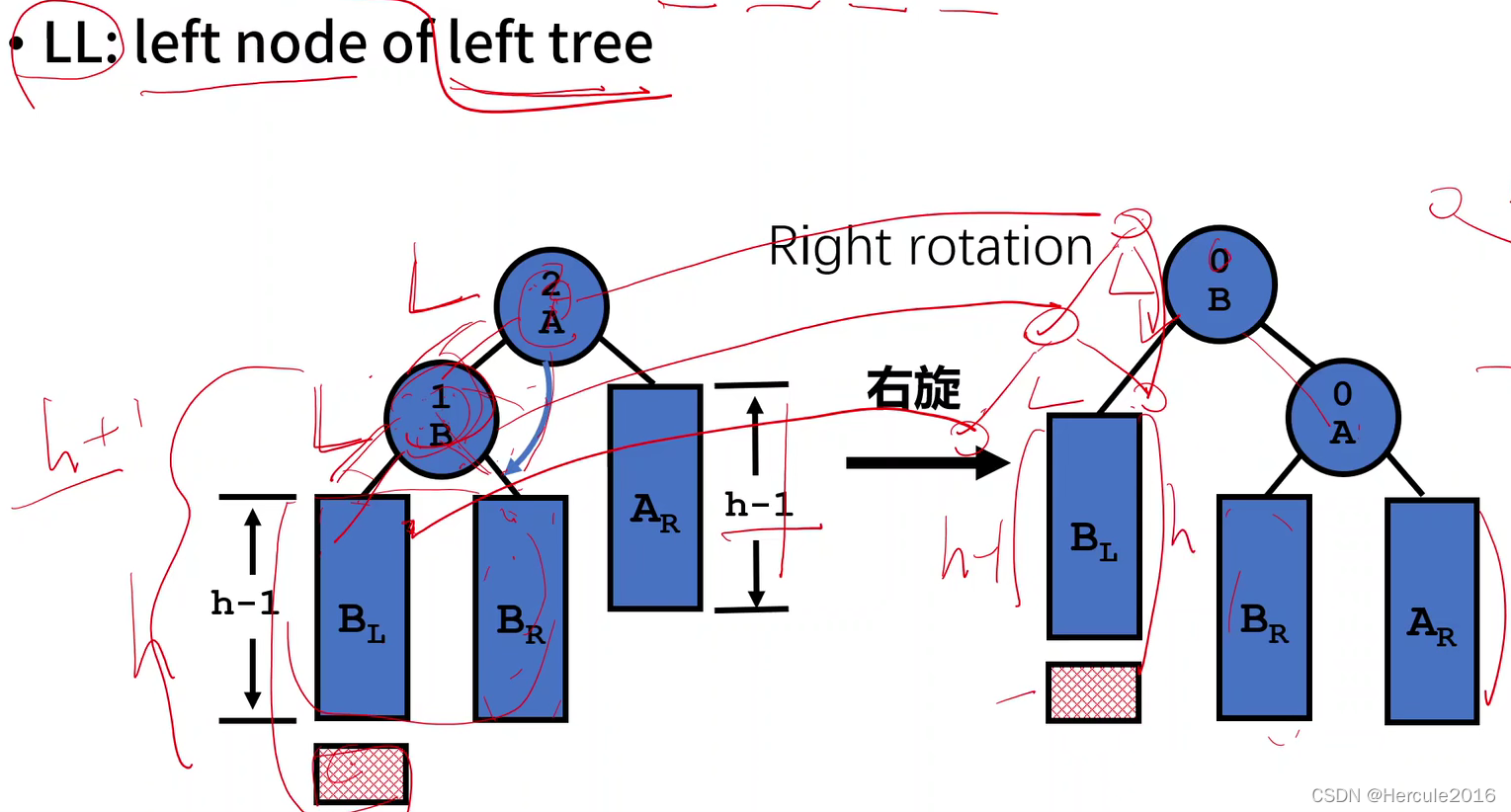
主要的失衡有LL型，就是左子树的左孩子失衡了，这时候就只需要对失衡的节点进行调整

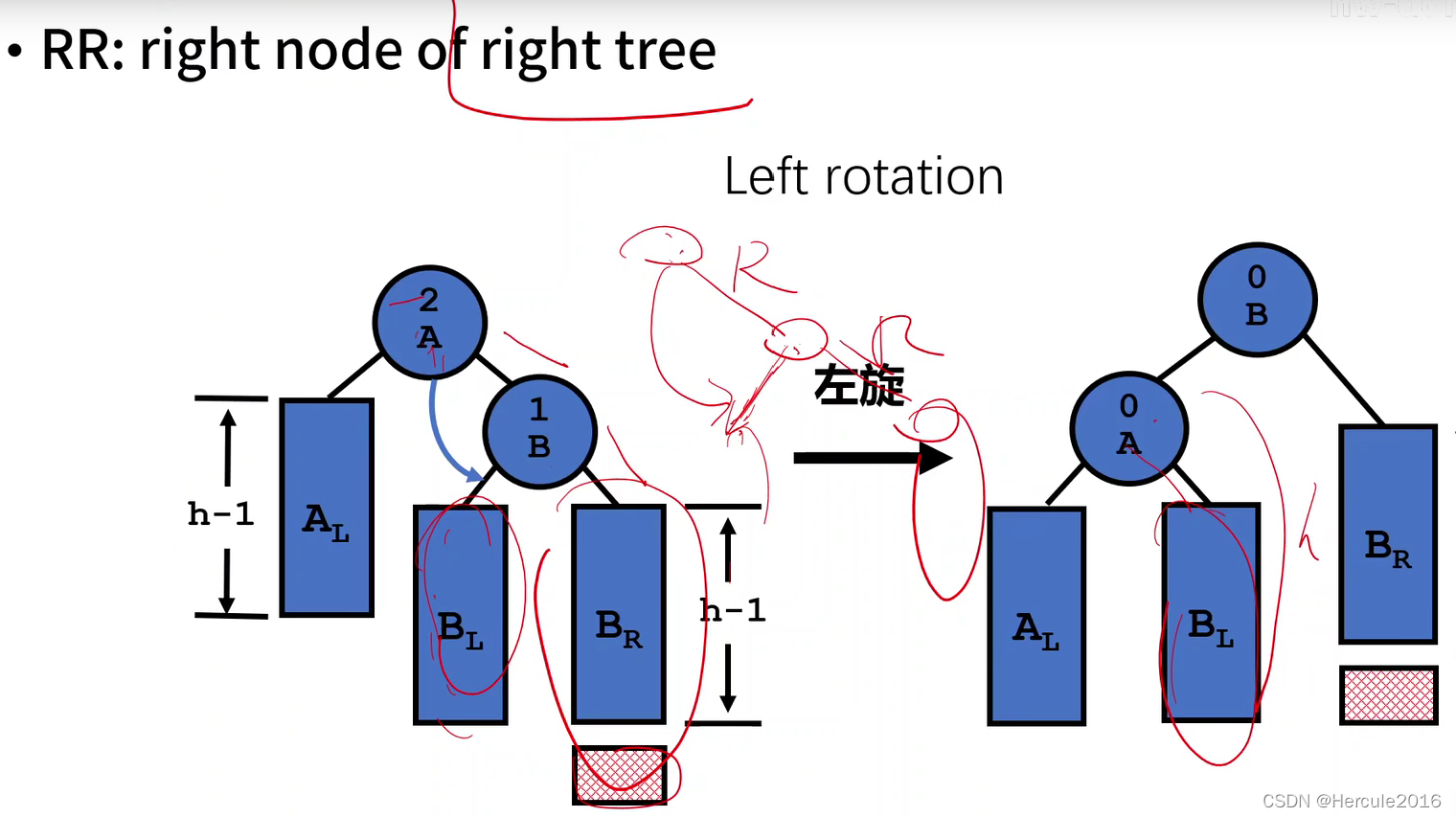
还有就是RR型也就是说右子树的右孩子在插入节点时候失衡了。

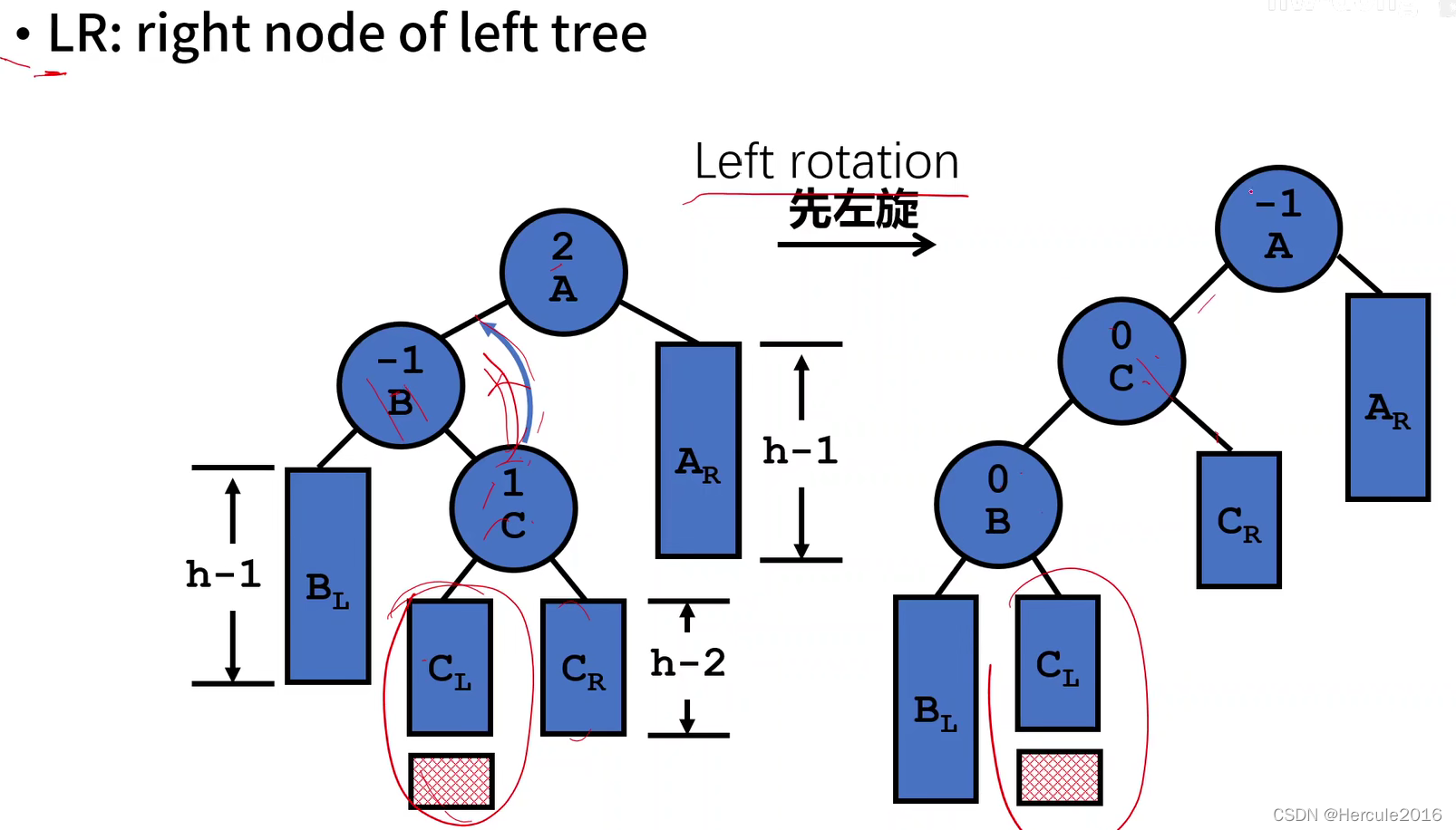
还有就是较为复杂的LR型失衡，也就是说失衡原因是左子树的右孩子上又插入了节点导致失衡，那么这种二叉树的调整步骤就是先转换为LL型失衡，然后再按照LL型失衡就行调整

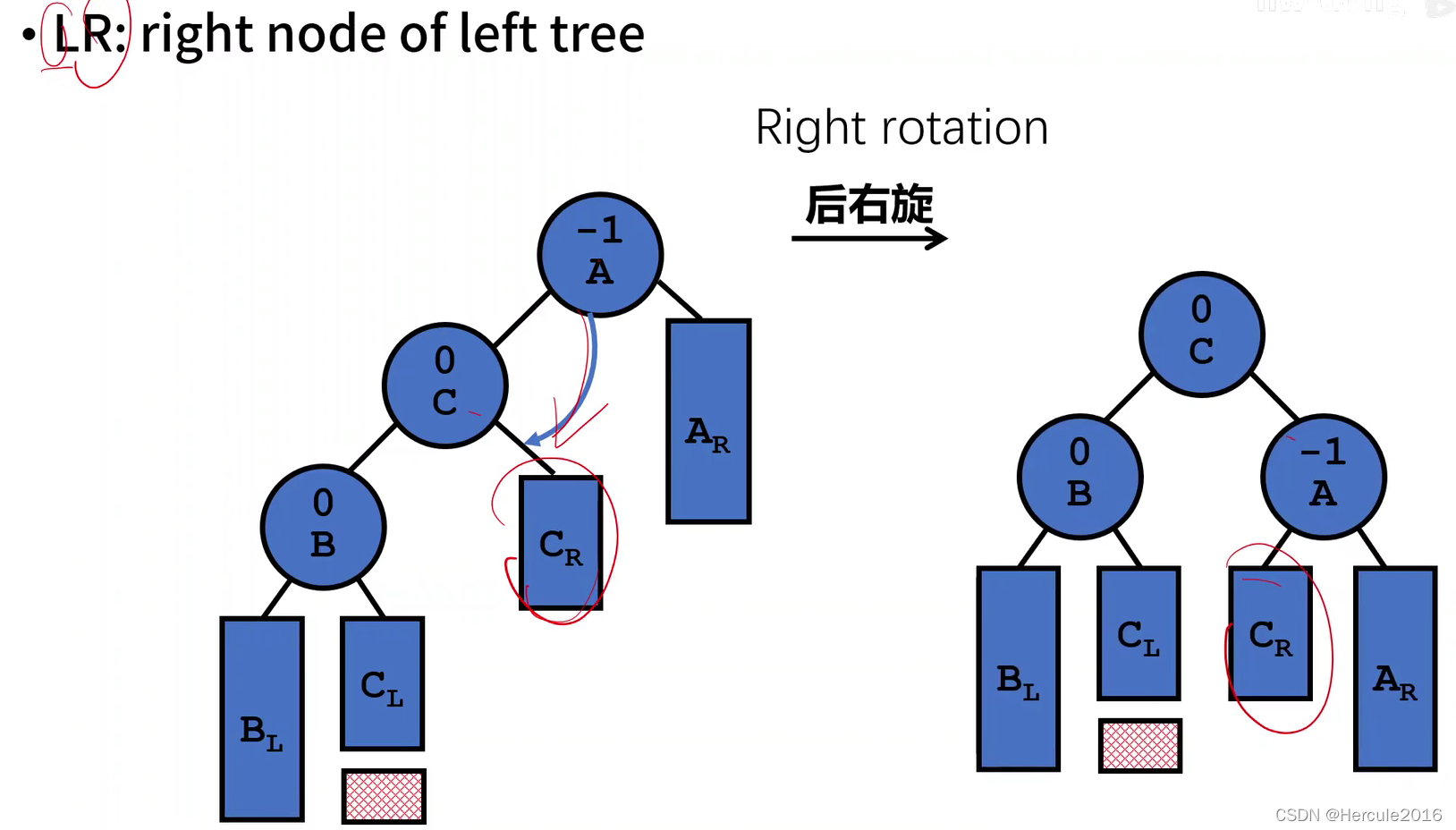
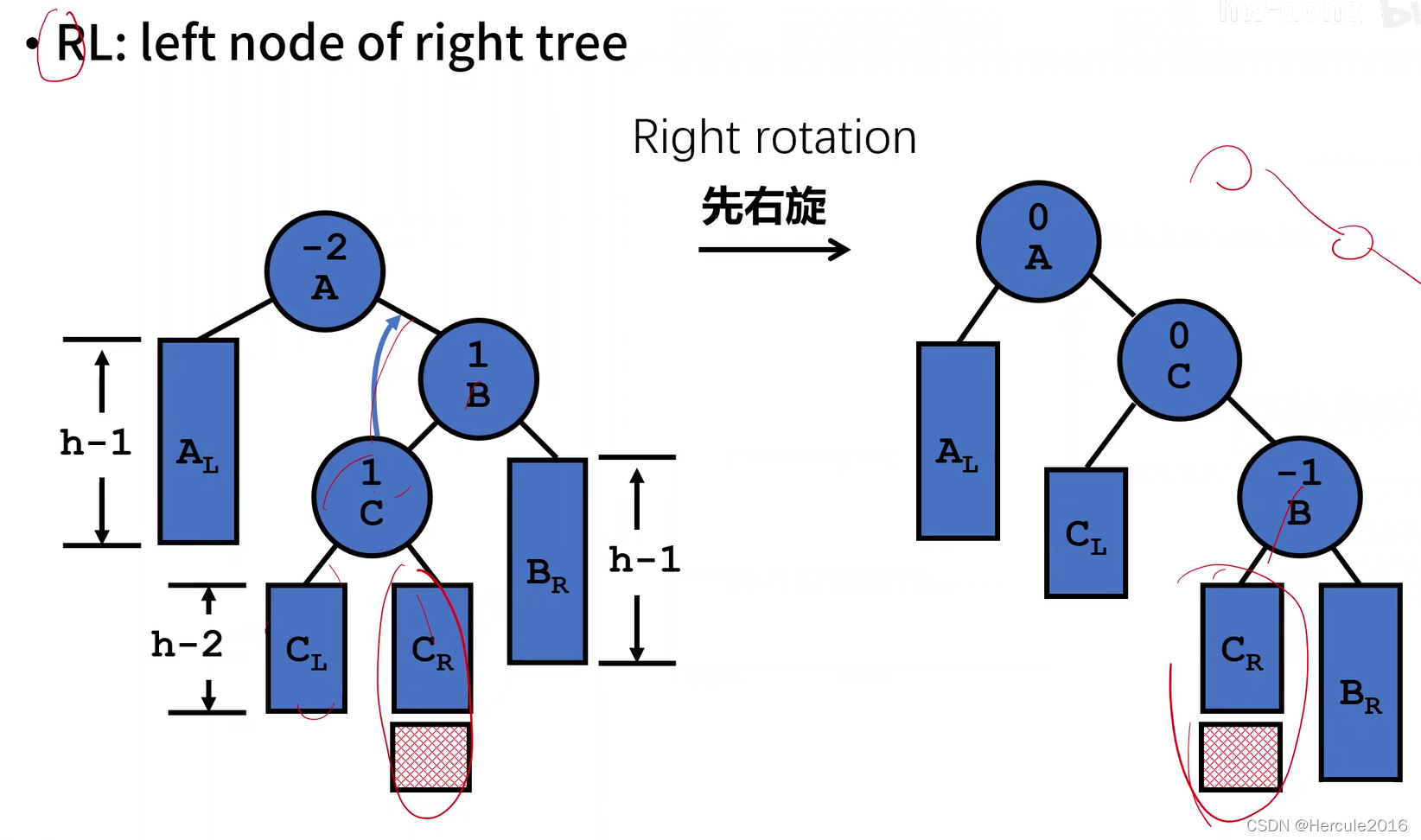
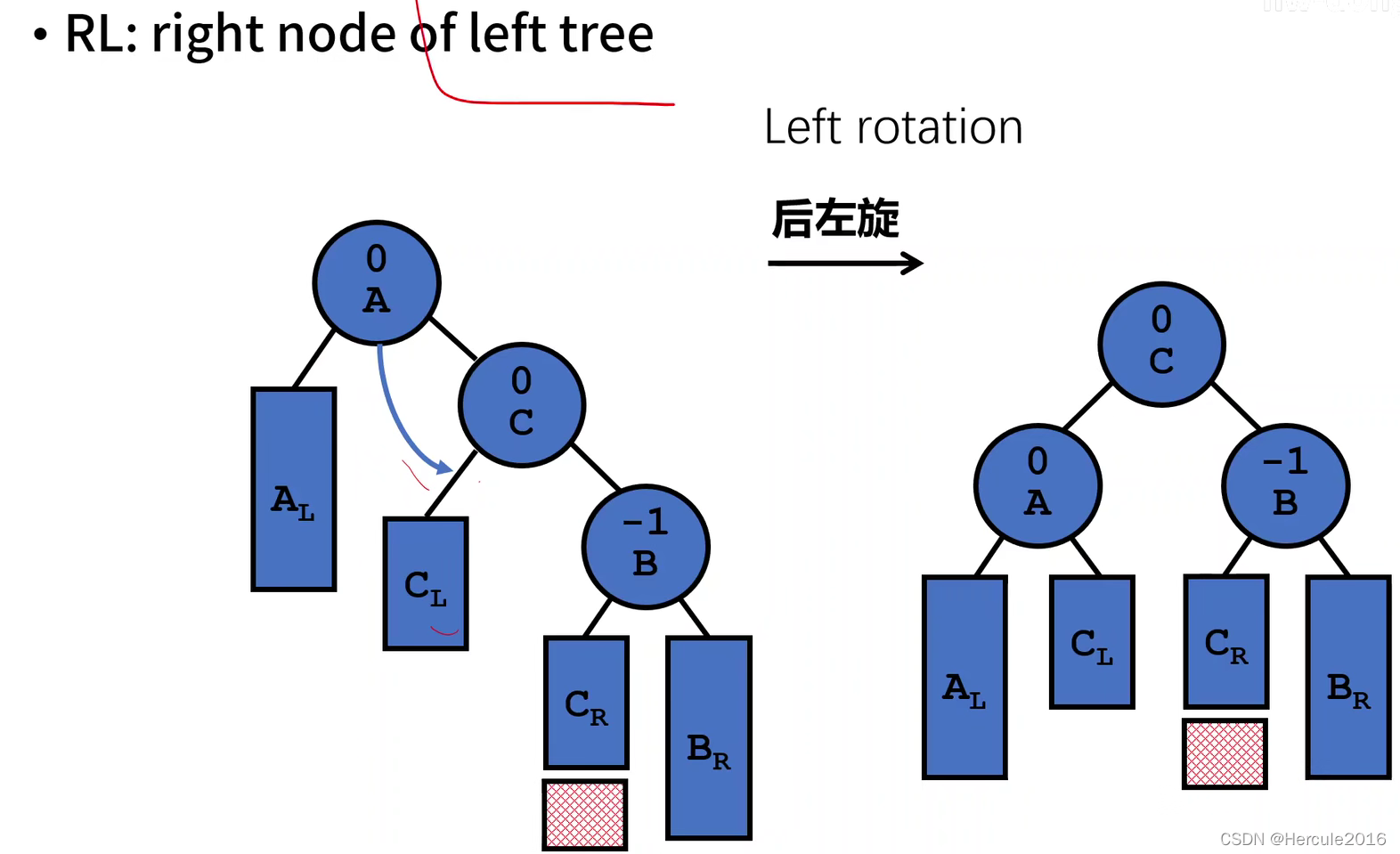
那么对于RL型失衡同理，我们所要做的就是把RL型失衡先调整为RR型失衡，而后再按照RR型失衡的套路进行调整

红黑树（Red-Black Tree–RBT）

对于平衡二叉树可以看到它有了足够好的查询效率，但是对于节点的插入和删除工作来说，虽然失衡调整没有原来的序列那样困难，但是还是需要比较复杂的算法。调整起来还是很费时间的，所以这时候引入了红黑树的概念
红黑树是一种自平衡的二叉查找树，它的平衡性没有AVL树好，并没有规定什么高度差小于1的概念约束。但是他有他自己的约束来保证树基本 上是平衡的。它是给每一个节点颜色，比如红色和黑色。
所以对于应用场景来说如果插入删除并不是很频繁,大部分的操作都是查找，那么我们就用AVL树。但是如果插入删除很频繁那么我们就用红黑树来实现。

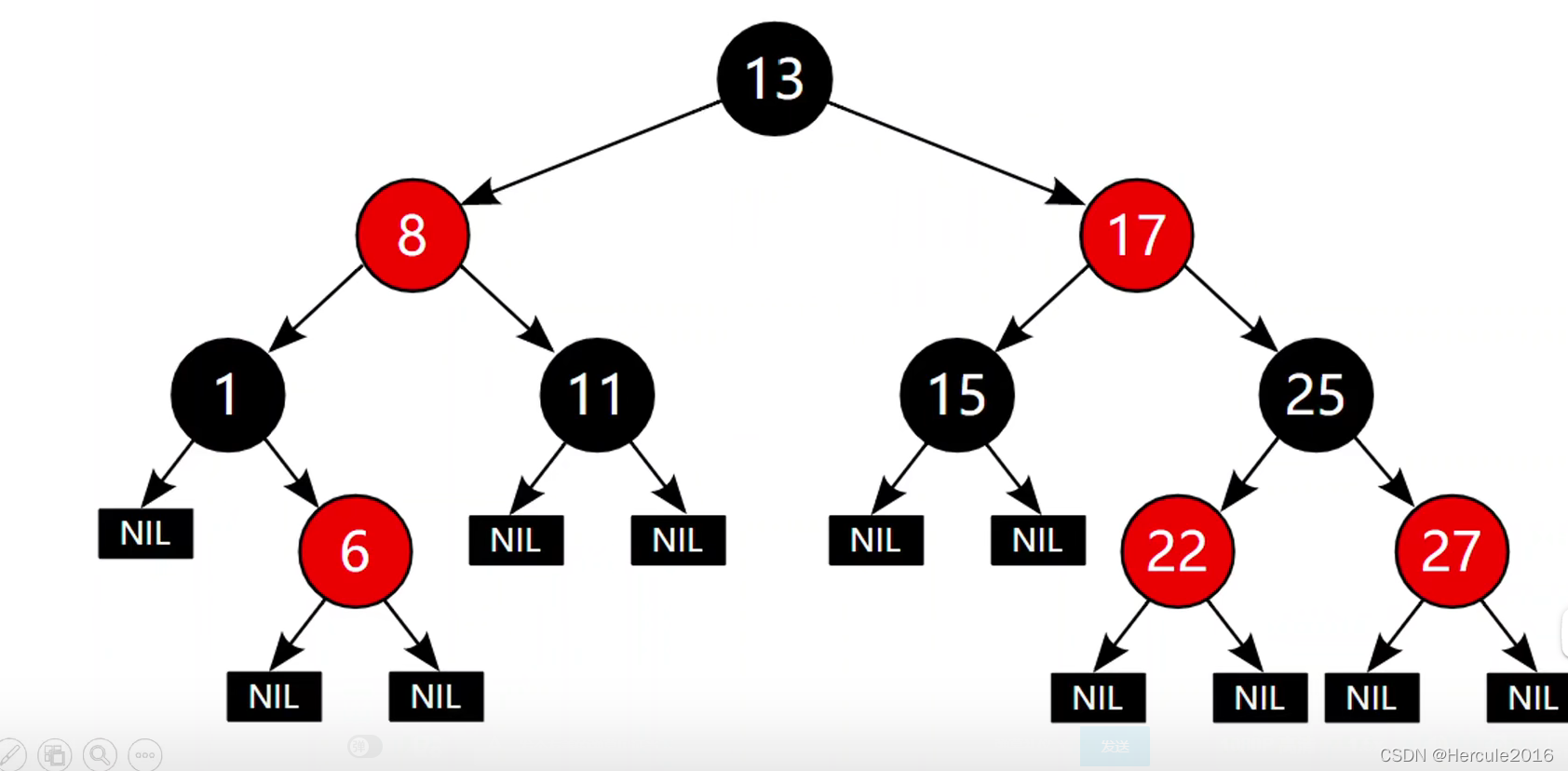
红给树每个节点都必须是有颜色的也就是红色或者黑色，
1、对于红黑树来说，红黑树的根节点必须是黑色的。
2、对于红色节点来说它的孩子必须是黑色的，这是红属性，也就是红色的不可能是两个红色的连在一起的，必须是红色的孩子不能是红色
3、对于红黑树来说，有一条重要的属性就是从根节点到他的任一叶子节点（红黑树的叶子节点与普通的二叉树不同，对于红黑树来说，空也算是一个叶子，就比如上图红色节点6的叶子节点是下面两个空节点）所经过的黑色节点的数目是相同的。就比如8他到所有的他的叶子节点都要经过1或者11也就是都要经过一个黑色节点。而从13到所有的叶子节点则都要经过两个黑色节点
4、整个树的高度不超过log2(n+1)

可以看到红黑树把空指针也算作了一个节点，这与一般的二叉查找树是不同的。他的叶子节点就是空指针，内部节点就是非空指针的点。
所有的这些特性保证了二叉平衡树基本是平衡的。

黑色高度
那么什么叫做黑色高度呢？黑色高度就是从任意一个节点x到他的叶子节点所需要经过的黑色节点的数目，就叫做黑色高度。

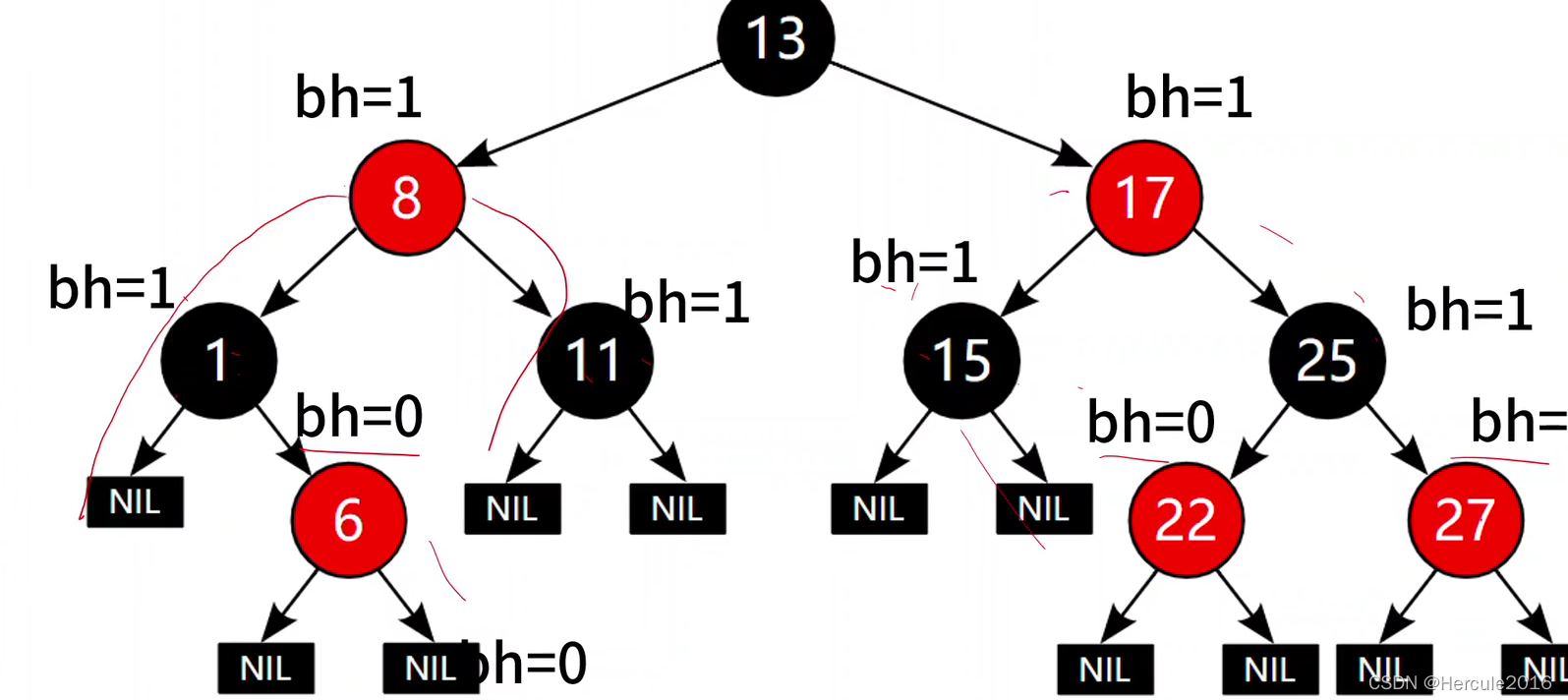
就像红色节点6到叶子节点所经过的黑色节点数目为0，则他的黑色高度（bh）就是0，那么类比红色节点6，黑色节点1和红色节点8所经过的黑色节点数目为1，因为黑色节点1本身就是黑色节点。

红黑树的性质有如下两条
1、任何一个节点的内部节点数目都至少有2^bh(x) -1个。
也就是说任一个节点内部节点的数目都至少有2的黑色高度次方减1个内部节点。

2、任何一个节点的高度有bh(x)>=h(x)/2
任何一个节点的黑色高度都大于等于树高度的二分之一

首先我们看第一个性质怎么证明，这个可以用上学的时候学的数学归纳法，
1）首先当一个节点的黑色高度是0的时候，那么它至少有根据公式此时他至少有0个内部节点
2）当一个节点黑色高度大于0的时候，如果此节点的孩子是红色的，那么他的孩子的黑色高度和他是一致的，那么如果这个节点的孩子是黑色的，那么孩子的黑色高度等于父亲的黑色高度减去1.
所以根据数学归纳法，
孩子节点肯定至少有2^bh(x) - 1个内部节点

而后对于第二个结论，因为红黑树的规则规定，是不能有两个连续的红色节点连接在一起的。所以必然有bh(x)>=h(x)/2

怎么往红黑树插入节点
1、如果树是空的，那么插入新节点的时候肯定是插入的黑色节点。
2、如果树不是空的，那么插入新节点作为叶子节点是红色的。
3、如果新插入的红色节点的父亲节点是红色的，那么就要检查父亲节点的兄弟节点，如果这个兄弟节点也是红色的那么就把父亲节点和父亲节点的兄弟节点都变黑色。
4、而后再检查新节点的父亲的父亲是不是根节点，如果是根节点那么颜色不变，否则就要重新着色。

还有一种情况就是
新插入的红色节点的父亲节点的兄弟节点是黑色的或者是空的

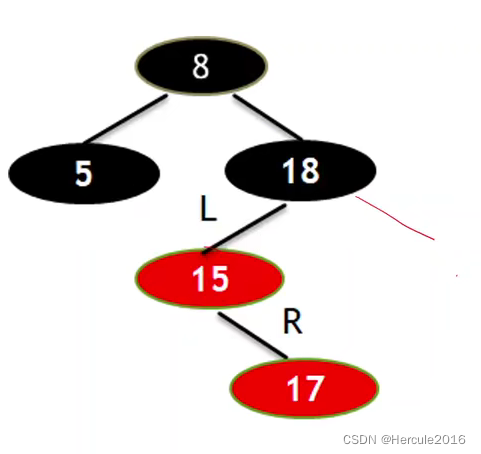
那么这个时候就需要做出调整，LR型的就要左旋。也就是调整成为LL型。

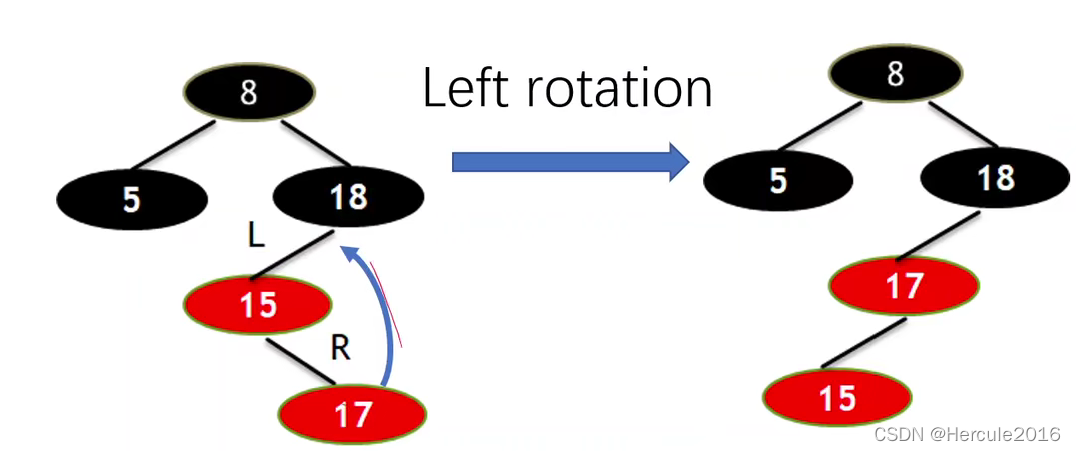
这时候再右旋一下

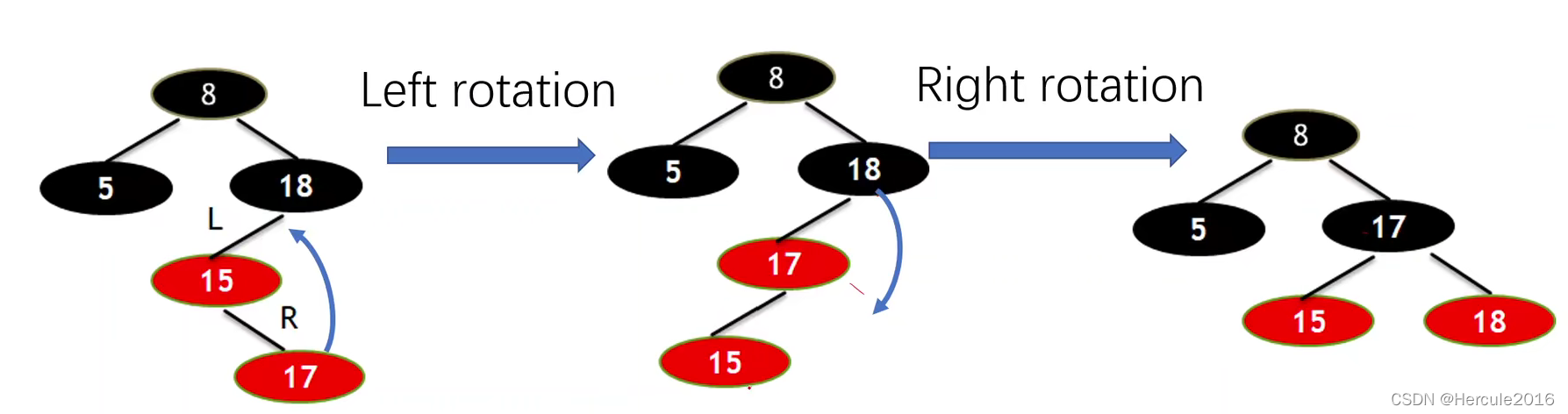
总结

• 如果插入节点时是空的，那么插入节点是黑色的并且成为根。
• 否则把着色节点为红色，并且检查以下两项
• 如果父亲是红色的，那么就检查父亲的兄弟是不是也是红色的。
• 如果是那就那就把父亲和父亲的兄弟的颜色全部转换，再看父亲的父亲节点是不是根节点如果不是根节点再转换颜色。
• 如果父亲是红色的，但是父亲的兄弟是黑色或者说是NULL那就要旋转

对于删除也是一样的

本人水平有限，整理水平业有限，参考b站视频做的整理，具体视频见：
b站视频地址
因为是我自己整理的我就投原创了，想喷就喷吧，对于网络我已经麻木了