（Java数据结构和算法）二叉搜索树

二叉搜索树

二叉搜索树的特点

• 若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
• 任意节点的右子树不空，则右子树上所有结点的值均大于等于它的根结点的值；
• 任意节点的左、右子树也分别为二叉查找树。

算法难点—删除操作

在二叉搜索树中插入节点、遍历二叉树、寻找最值，这些操作是很容易的，难点是删除一个节点。 删除一个节点包含三种情况：

（1）该节点左右子节点都为空。直接把该节点对应孩子搞空。

（2）该节点只有一个子节点（左子节点或右子节点），对应父节点指向对应该节点的对应孩子。

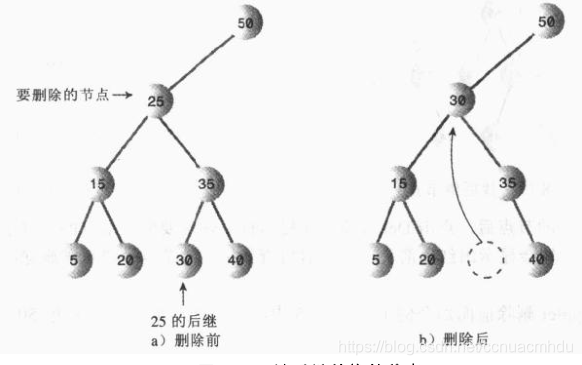
（3）该节点有左右两个子节点，用中序后继节点替换该节点。

算法实现

//节点类
class Node{
	public int e;//节点值
	public Node leftChild;//左孩子
	public Node rightChild;//右孩子
}

class Tree{

	private Node root;//树根
	
	public Tree(){
		root = null;
	}	
	//按节点值查找节点
	public Node find(int key){
		if(root == null){//空树
			return null;
		}
		Node current = root;
		while(current.e != key){
			if(key < current.e){
				current = current.leftChild;
			}else{
				current = current.rightChild;
			}
			if(current == null){
				return null;
			}
		}
		return current;
	}
	//插入节点
	public void insert(int e){
		Node newNode = new Node();
		newNode.e = e;
		if(root == null){
			root = newNode;
		}else{
			Node current = root;
			Node parent = null;
			while(true){
				parent = current;
				if(e < current.e){
					current = current.leftChild;
					if(current == null){
						parent.leftChild = newNode;
						return;
					}
				}else{
					current = current.rightChild;
					if(current == null){
						parent.rightChild = newNode;
						return;
					}
				}
			}
		}
	}

	//删除
	public boolean delete(int e){
		if(root == null){//如果树本身是空的
			return false;
		}

		Node current = root;//用于存放待删除节点
		Node parent = root;//用于存放待删除节点的父节点
		boolean isLeftChild = true;//判断待删除节点是不是其父节点的左子节点
		//先找到待删除的节点
		while(current.e != e){
			parent = current;
			if(e < current.e){
				isLeftChild = true;
				current = current.leftChild;
			}else{
				isLeftChild = false;
				current = current.rightChild;
			}
			if(current == null){
				return false;	
			}
		}
		
		//经过上面的while循环找到了待删除的节点current和其父亲节点parent
		//下面根据待删除节点的三种情况，分别进行待删除节点的删除操作
		
		//1.待删除节点的左右两个子节点都空
		if(current.leftChild == null && current.rightChild == null){
			if(current == root){//如果待删除的节点是树根，是树根，不会进入while循环
				root = null;
			}else if(isLeftChild){//如果待删除的节点是其父节点的左子节点
				parent.leftChild = null;
			}else{//如果待删除节点是其父节点的右子节点
				parent.rightChild = null;
			}
		}else if(current.rightChild == null){//2.待删除节点的左子节点非空，右子节点为空
			if(current == root){
				root = current.leftChild;
			}else if(isLeftChild){
				parent.leftChild = current.leftChild;
			}else{
				parent.rightChild  = current.leftChild;
			}
		}else if(current.leftChild == null){//3.待删除节点的右子节点非空，左子节点为空
			if(current == root){
				root = current.rightChild;
			}else if(isLeftChild){
				parent.leftChild = current.rightChild;
			}else{
				parent.rightChild = current.rightChild;
			}
		}else{//4.待删除节点的左右节点均非空，用待删除节点的中序后继节点代替待删除节点
				
			//找到待删除节点的中序后继节点，待删除节点的父亲节点指向待删除节点的中序后继节点
			Node successor = getSuccessor(current);
			if(current == root){
				root = successor;
			}else if(isLeftChild){
				parent.leftChild = successor;
			}else{
				parent.rightChild = successor;
			}
			//将中序后继节点的左子节点指向待删除节点的左子节点
			successor.leftChild = current.leftChild;
		}

		return true;
	}
	//寻找待删除节点的中序后继节点，并将中序后继节点的右子节点指向待删除节点的右子节点
	private Node getSuccessor(Node delNode){
		Node successorParent = delNode;//中序后继节点的父节点，用于指向中序后继节点的右子节点
		Node successor = delNode;
		Node current = delNode .rightChild;
		while(current != null){//中序后继左子节点必定是两个子节点为空，或仅含有右子节点
			successorParent = successor;
			successor = current;
			current = current.leftChild;
		}
		if(successor != delNode.rightChild){//如果中序后继节点不是待删除节点的右子节点，即待删除节点
				//的右子节点存在左子节点
			//要处理一下中序后继节点的右子节点
			successorParent.leftChild = successor.rightChild;
			successor.rightChild = delNode.rightChild;
		}
		return successor;
	}
	//遍历
	public void traverse(){
		
			System.out.println("PreOrder traverse: ");
			preOrder(root);
			System.out.println();
			System.out.println("InOrder traverse:");
			inOrder(root);
			System.out.println();
			System.out.println("PostOrder traverse:");
			postOrder(root);		
			System.out.println();
	}
	//先序遍历
	private void preOrder(Node localRoot){
		if(localRoot != null){
			System.out.print(localRoot.e+" ");
			preOrder(localRoot.leftChild);
			preOrder(localRoot.rightChild);
		}
	}
	//中序遍历
	private void inOrder(Node localRoot){
		if(localRoot != null){
			inOrder(localRoot.leftChild);
			System.out.print(localRoot.e+" ");
			inOrder(localRoot.rightChild);
		}
	}
	//后序遍历
	private void postOrder(Node localRoot){
		if(localRoot != null){
			postOrder(localRoot.leftChild);
			postOrder(localRoot.rightChild);
			System.out.print(localRoot.e+" ");
		}
	}

	public Node maximum(){
		if(root == null){
			return null;
		}
		Node current = root, obj = null;
		while(current != null){
			obj = current;
			current = current.rightChild;
		}
		return obj;
	}
	public Node minimum(){
		if(root == null){
			return null;
		}
		Node current = root, obj = null;
		while(current != null){
			obj = current;
			current = current.leftChild;
		}
		return obj;
	}
	
}

public class Main {

	public static void main(String[] args){
		Tree tree = new Tree();
		int[] a = {4,2,1,5,9,6};
		for(int i = 0; i < a.length; i++){
			tree.insert(a[i]);
		}
		tree.traverse();
		//查找5
		Node node1 = tree.find(5);
		if(null != node1){
			System.out.println(node1.e+" found.");
		}else{
			System.out.println("not found.");
		}
		//删除5
		System.out.println("5 is deleted?"+tree.delete(5));
		tree.traverse();
		
		Node max = tree.maximum();
		Node min = tree.minimum();
		if(max != null){
			System.out.println("max: "+ max.e);
		}
		if(min != null){
			System.out.println("min: "+min.e);
		}
	}
	
}

数组表示树

某节点索引是i，那么他的父节点是(i-1)/2，他的左子节点是2i+1，他的右子节点是2i+2