在初等数学中学习了三角形,四边形,多边形的面积计算:

现在来学习 的面积是如何定义的,以及如何计算的:
的面积是如何定义的,以及如何计算的:

1 抛物线下的曲边梯形
1.1 问题
之前介绍过,要求 ,
,![x\in[0,a]](https://i-blog.csdnimg.cn/blog_migrate/5d417809640c47493f56fee67c93bb4f.png) 之间的曲边梯形的面积
之间的曲边梯形的面积 :
:

可以把![[0,a]](https://i-blog.csdnimg.cn/blog_migrate/d4bd1a90679540c59f0e95dc1ccd025d.png) 均分为
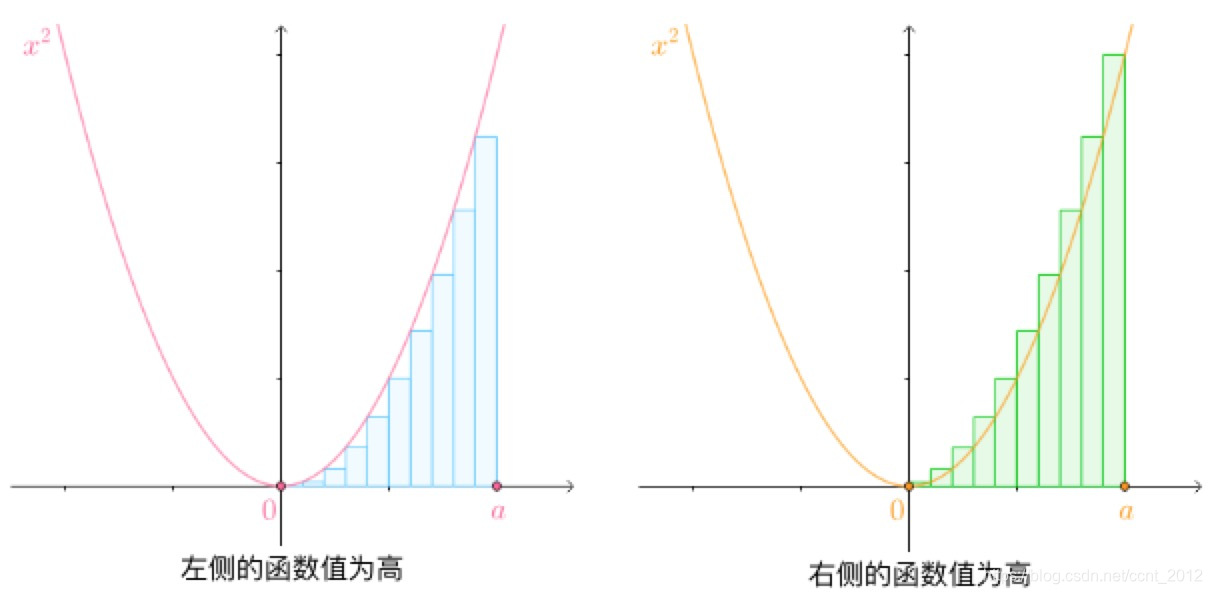
均分为 份,以每一份线段为底,以这一份线段的右侧的函数值为高做矩形:
份,以每一份线段为底,以这一份线段的右侧的函数值为高做矩形:

当 的时候,矩形面积和就是曲面下的面积:
的时候,矩形面积和就是曲面下的面积:
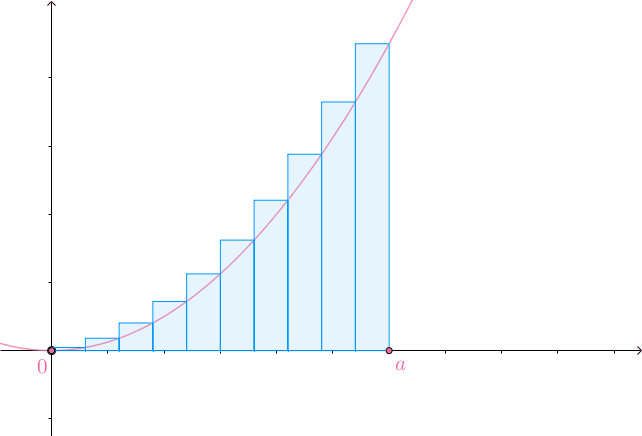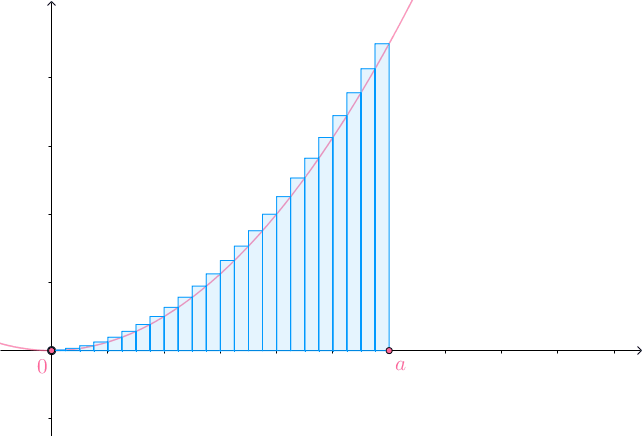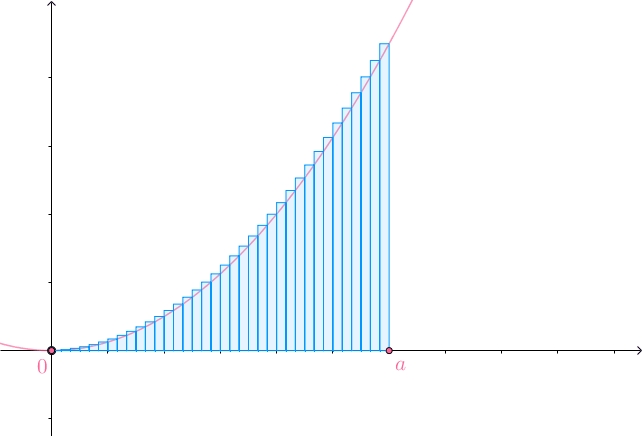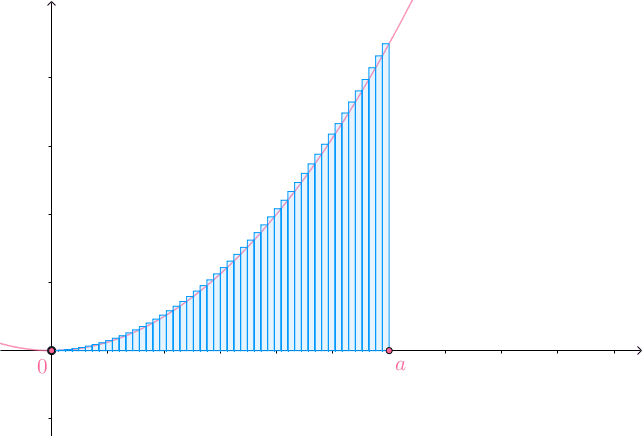
那么,能不能以这一份的线段的左侧的函数值为高做矩形?
1.2 计算
算一算就知道了。先把![[0,a]](https://i-blog.csdnimg.cn/blog_migrate/d4bd1a90679540c59f0e95dc1ccd025d.png) 均分成
均分成 份,每份长为
份,每份长为 ,以及各个划分点的坐标如下:
,以及各个划分点的坐标如下:

把坐标组成两个集合:

因此,以左侧的函数值为高的矩形和可以如下计算:

同样的道理,可以得到以右侧的函数值为高的矩形和:
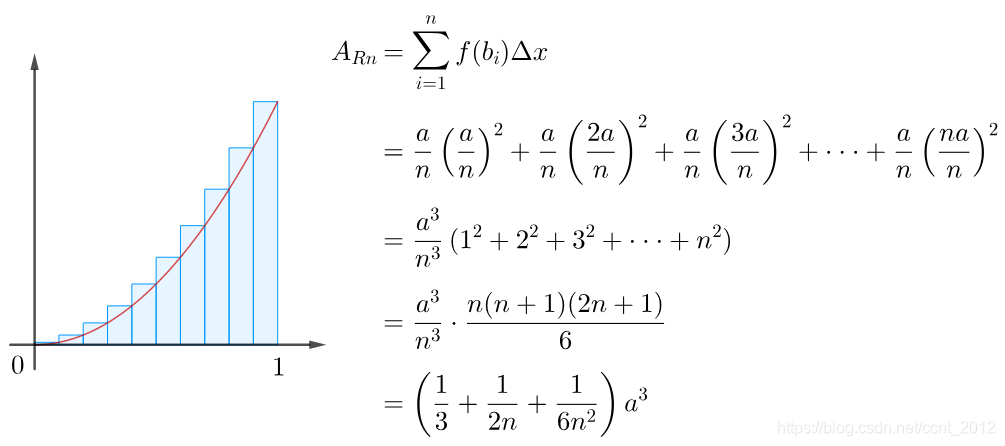
当 的时候,两者是相等的,它们都是曲边梯形的面积:
的时候,两者是相等的,它们都是曲边梯形的面积:

2 狄利克雷函数的曲边梯形
之前介绍连续的时候就介绍过狄利克雷函数:

也见识过它的古怪性质。这里也要把它拉出来作一个反面典型。 的图像是没有办法画的,非要画也就是这样的:
的图像是没有办法画的,非要画也就是这样的:

假设要求![[0,1]](https://i-blog.csdnimg.cn/blog_migrate/6179aae8b80f0596707e6d29907d220a.png) 内的曲边梯形面积,尝试对
内的曲边梯形面积,尝试对![[0,1]](https://i-blog.csdnimg.cn/blog_migrate/6179aae8b80f0596707e6d29907d220a.png) 进行
进行 等分,那么等分点必然为有理数点(下图为了演示方便,调整了下
等分,那么等分点必然为有理数点(下图为了演示方便,调整了下 坐标的比例):
坐标的比例):
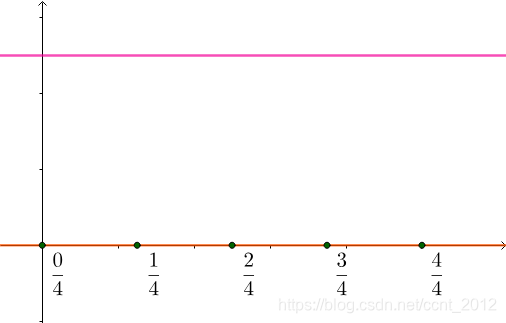
所以这些等分点的函数值必然为1。以1为高,以等分区间长度为底作矩形,可以得到:
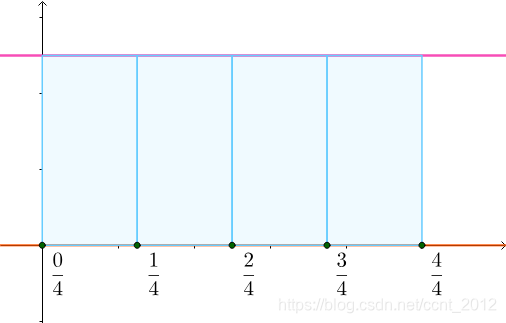
这些矩形的和必然为1,可以想象进行 等分也依然为1,所以有:
等分也依然为1,所以有:
下面换一种划分方式,以邻近的两个无理数作为端点划分区间,这些区间的端点的函数值必然为0,以区间长度为底,0为高,得到的矩形和为:
可见,对于 而言,不同的划分区间、不同的高的取法,会导致不同的矩形和:
而言,不同的划分区间、不同的高的取法,会导致不同的矩形和:
3 黎曼和

格奥尔格·弗雷德里希·波恩哈德·黎曼(1826-1866)是德国数学家,黎曼几何学创始人,复变函数论创始人之一。在数学界搞风搞雨的黎曼猜想也是他的杰作。
基于对刚才两种情况:
-
抛物线下的曲边梯形
-
狄利克雷函数下的曲边梯形
的思考,看到不同划分带来的效果,黎曼先发明了黎曼和,进而定义了曲边梯形的面积,也就是定积分。
3.1 任意划分
![[a,b]](https://i-blog.csdnimg.cn/blog_migrate/9644dd42dae4db40bc8b42c5e213bb0c.png) 不一定需要均分为
不一定需要均分为 份,可以任意分割:
份,可以任意分割:
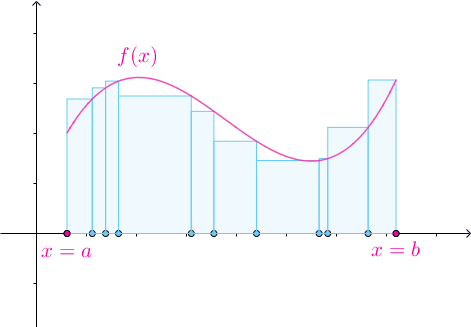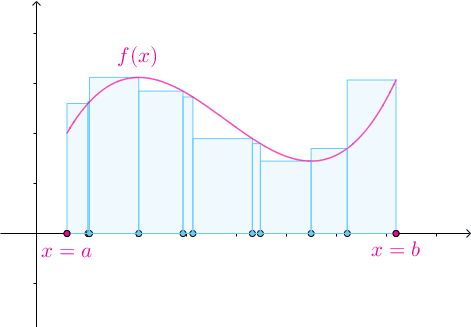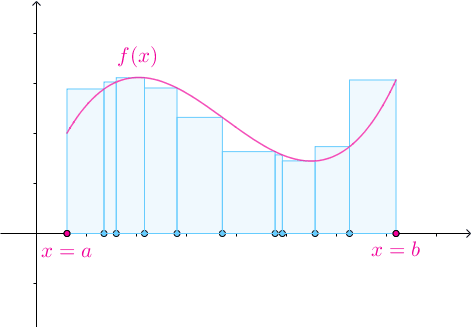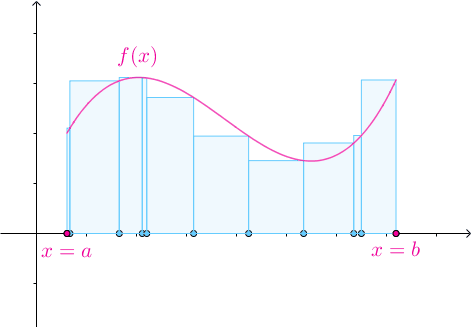
很显然用于分割区间的点符合:

令 ,那么集合:
,那么集合:

称为![[a,b]](https://i-blog.csdnimg.cn/blog_migrate/9644dd42dae4db40bc8b42c5e213bb0c.png) 的一个
的一个 。划分
。划分 定义了
定义了 个子区间:
个子区间:
![[x_0, x_1], [x_1, x_2], \cdots,[x_{k-1}, x_k],\cdots, [x_{n-1}, x_n]](https://i-blog.csdnimg.cn/blog_migrate/44a63937a38c1aecf5f5aadf9cd5d34d.png)
![[x_0, x_1]](https://i-blog.csdnimg.cn/blog_migrate/e35cf6a71d1331537b403dde200350f5.png) 称为第
称为第 个子区间,更一般的
个子区间,更一般的![[x_{k-1},x_k]](https://i-blog.csdnimg.cn/blog_migrate/e0643cb2243e3693f848f4e83be2f2a6.png) 被称为第
被称为第 个子区间:
个子区间:

第 个子区间的长度为
个子区间的长度为 :
:

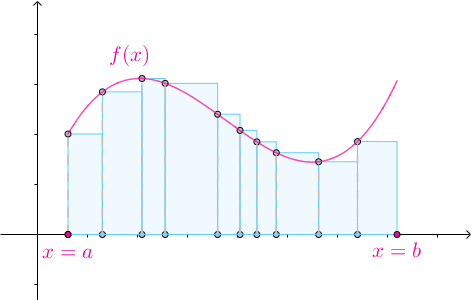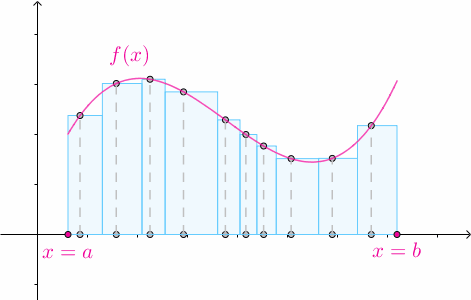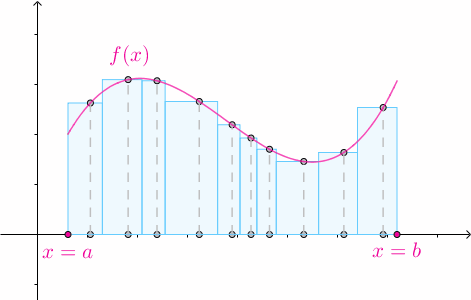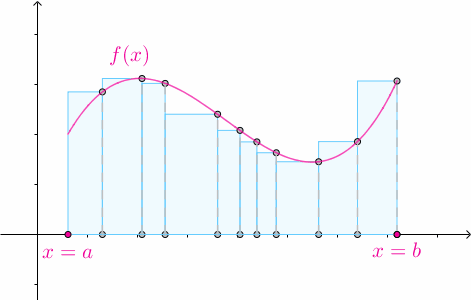
3.2 任意高度
对于某一个划分 ,在其第
,在其第 个子区间内随便选一个数
个子区间内随便选一个数 :
:

以 作为矩形的高:
作为矩形的高:

那么矩形的高度也可以是任意的:
3.3 黎曼和
根据刚才的讲解,可以得到如下定义:
设函数在
上有定义,在
上任意插入若干个分点:
这些分点的集合:
称为
的一个
。划分
定义了
个子区间:
它们的长度依次为:
在每个子区间
上任取选取一个数
,以
为底,
为高构造矩形,这些矩形的和:
称为
在
上的
。
之前计算的 、
是黎曼和:
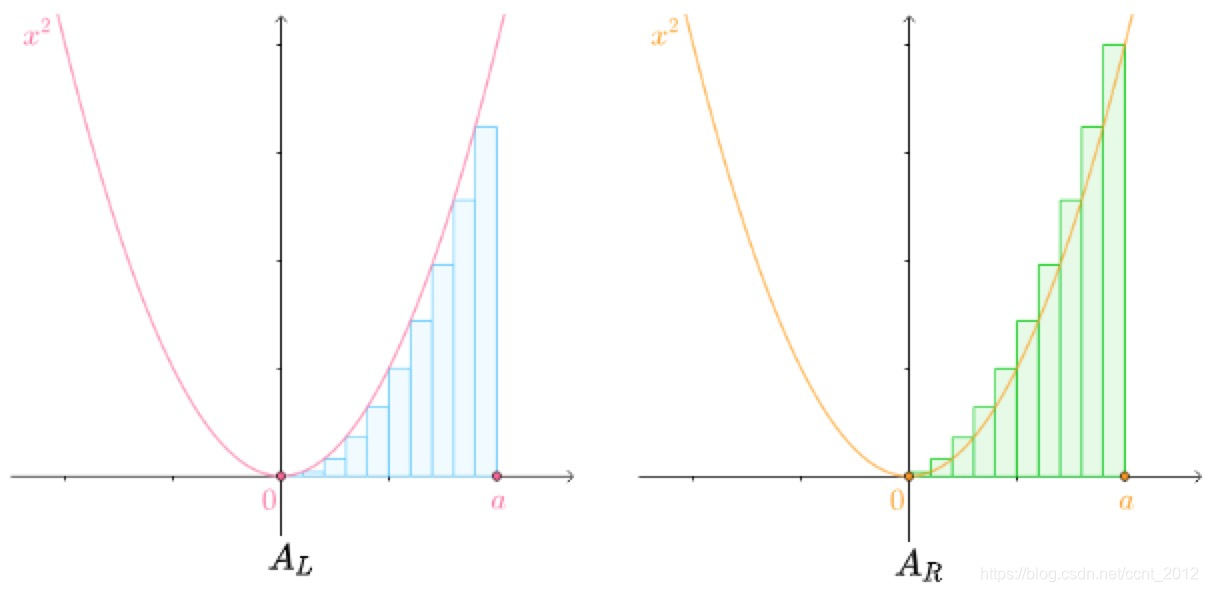
狄利克雷函数中划分出来的矩形和 、
也是黎曼和。
4 定积分
随着![[a,b]](https://i-blog.csdnimg.cn/blog_migrate/9644dd42dae4db40bc8b42c5e213bb0c.png) 的划分不断变细,所有子区间的长度趋于0时,黎曼和不断地逼近曲边梯形的面积:
的划分不断变细,所有子区间的长度趋于0时,黎曼和不断地逼近曲边梯形的面积:
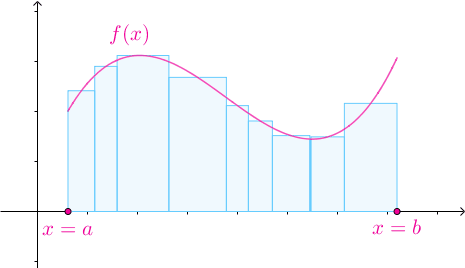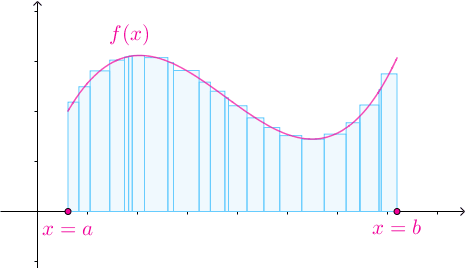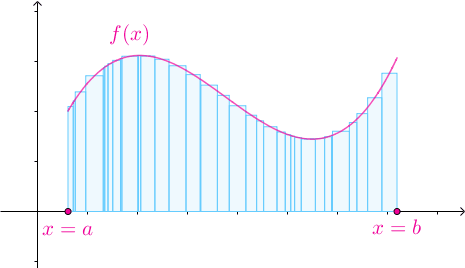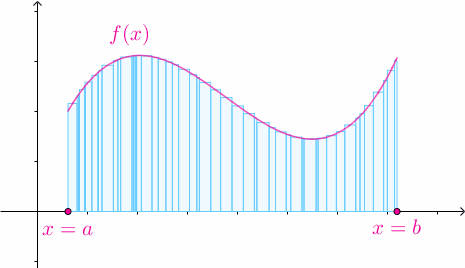
这个过程的严格化如下:
设函数在
上有定义,对于
上的任意划分
,
为子区间
上任意选取的数,子区间
的长度为
,记:
如果下述极限存在:
则称
在
上
,
为
,
为
,
为
在
上的
,
为
,可以标记如下:
回到之前讨论的问题:
-
抛物线下的曲边梯形:
,以及各种划分都相等,所以
 存在,可积
存在,可积 -
狄利克雷函数下的曲边梯形:
,所以
 不存在,不可积
不存在,不可积
这里新引入的积分符号是莱布尼兹创造的:

其中, 代表英文中的求和(“sum”),拉长的
代表英文中的求和(“sum”),拉长的 则表明积分是和的极限(“limits of sums”)。这个符号相当精练,可以表达非常丰富的信息:
则表明积分是和的极限(“limits of sums”)。这个符号相当精练,可以表达非常丰富的信息:

最新版本(可能有不定期更新):黎曼和与定积分





 本文探讨了曲边梯形面积的计算,介绍了通过黎曼和逼近面积的概念。从抛物线下曲边梯形到狄利克雷函数的特殊情况,展示了不同划分方式对面积计算的影响。最终,通过黎曼和的定义,引出了定积分的概念。
本文探讨了曲边梯形面积的计算,介绍了通过黎曼和逼近面积的概念。从抛物线下曲边梯形到狄利克雷函数的特殊情况,展示了不同划分方式对面积计算的影响。最终,通过黎曼和的定义,引出了定积分的概念。

![[x_0, x_1], [x_1, x_2], \cdots, [x_{n-1}, x_n]](https://i-blog.csdnimg.cn/blog_migrate/e35cf6a71d1331537b403dde200350f5.png%2C%20%5Bx_1%2C%20x_2%5D%2C%20%5Ccdots%2C%20%5Bx_%7Bn-1%7D%2C%20x_n%5D)






















 635
635












