如何用范德蒙行列式完成插值

最新推荐文章于 2025-02-28 15:13:10 发布

原创最新推荐文章于 2025-02-28 15:13:10 发布 · 1.3k 阅读

10 ·

CC 4.0 BY-SA版权

文章标签：

#线性代数 #行列式

线性代数专栏收录该内容

13 篇文章

订阅专栏

本文介绍了如何使用范德蒙行列式进行插值，以解决天文观测中的数据缺失问题。通过建立坐标系和假设3次多项式曲线，利用已知的4个观测点，求解出星期三火星与地球的距离。最终得出星期三火星距离地球为3.5万公里。此外，还提及了其他插值方法如牛顿插值法和拉格朗日插值法。

部署运行你感兴趣的模型镜像

如何用范德蒙行列式完成插值

同学们大家好，今天我们来讲解一个范德蒙行列式的应用--插值

1 什么是插值

插值问题是天文领域中，经常碰到的一个数学问题。比如某天文爱好者，每天都观察火星离地球的距离。星期一，星期二，星期四，星期五天气不错，成功观测到了数据,分别是3万公里，5万公里，2万公里与4万公里(数字纯属虚构)。但星期三因为有雾霾，没有观测到数据。

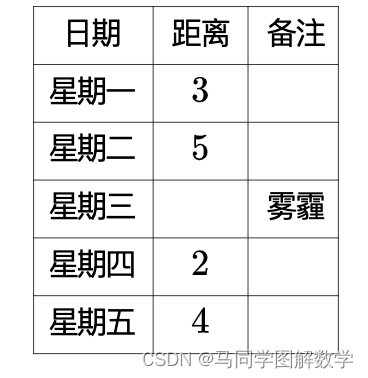
下面，我们希望利用星期一，二，四，五的数据，求出星期三的数据。这种，通过已知的离散数据求未知数据的过程或方法就称为插值

2 思路

下面。我们以横坐标为日期，纵坐标为距离，建立一个坐标系。然后将表格中的数据表示在坐标系中

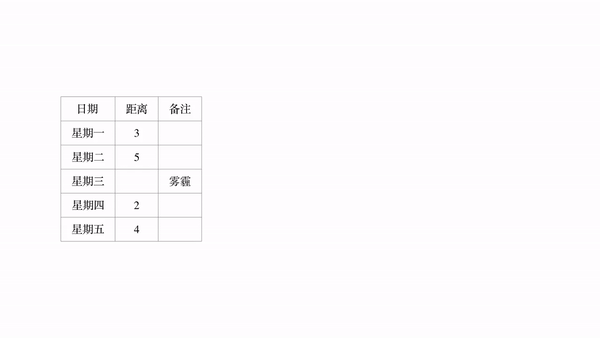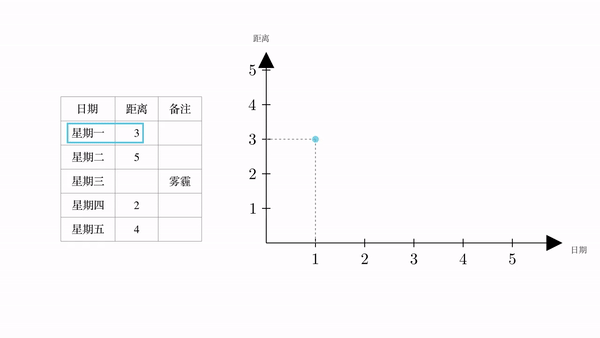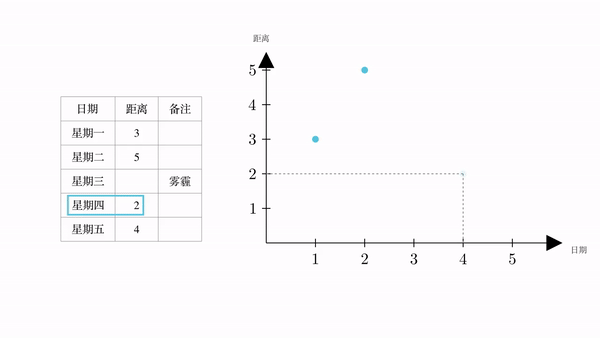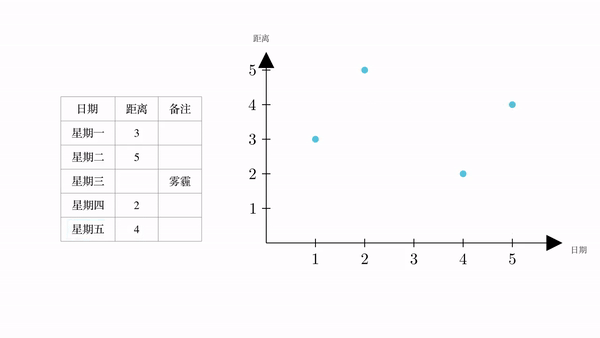
根据常识，火星一定是连续运动的，会形成一个运动轨迹。而我们现在已知的4个点，必定在这个运动轨迹上。

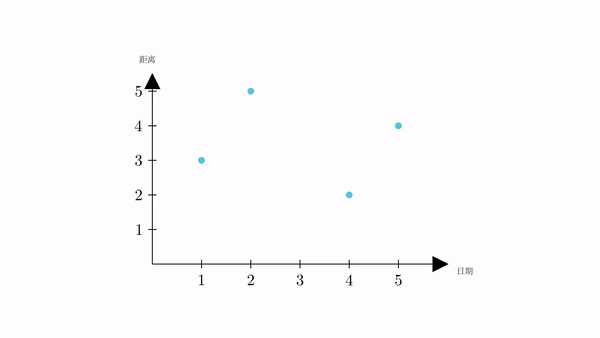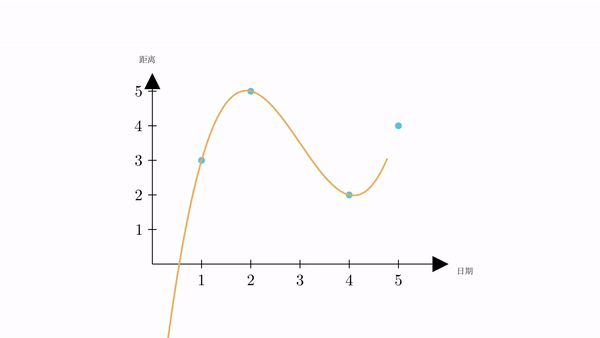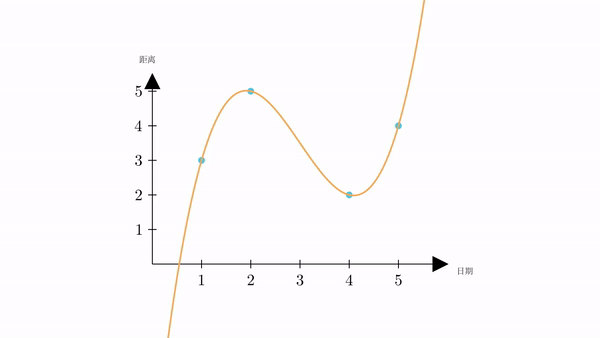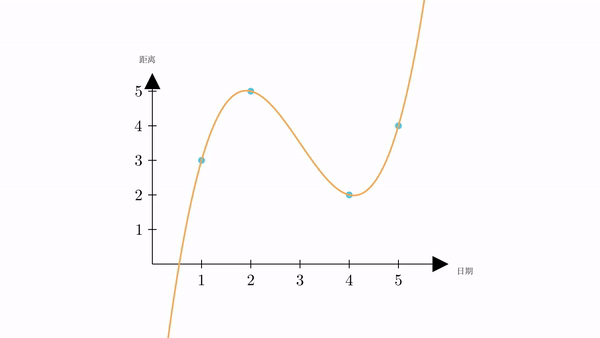
只要我们将轨迹求出来，那我们就可以根据它，求出星期三时的距离。

3 求解

因为要穿越的已知点是4个，那么可以假设描述轨迹的曲线为3次多项

$y=a_0+a_1x+a_2x^2+a_3x^3$

将四个点的值带入多项式，可以得到如下方程组

$\begin{cases}3=a_0+1a_1+1^2a_2+1^3a_3\\ 5=a_0+2a_1+2^2a_2+2^3a_3\\ 2=a_0+4a_1+4^2a_2+4^3a_3\\ 4=a_0+5a_1+5^2a_2+5^3a_3\\ \end{cases}$

可以看到此时系数矩阵的行列式，就是范德蒙行列

$|\boldsymbol{A}|=\begin{vmatrix}1&1&1^2&1^3\\ 1&2&2^2&2^3\\ 1&4&4^2&4^3\\ 1&5&5^2&5^3\end{vmatrix}$

下面我们就依靠范德蒙行列式来求解方程。

解:(1)根据范德蒙行列式的运算规则，可以得到系数矩阵

$\boldsymbol{A}=72$

因为系数矩阵不为零。可知方程组有唯一解

(2)根据克拉默法则可知

$a_0=\frac{|\boldsymbol{A}_1|}{\boldsymbol{A}}\quad a_1=\frac{|\boldsymbol{A}_2|}{\boldsymbol{A}}$

$a_2=\frac{|\boldsymbol{A}_2|}{\boldsymbol{A}}\quad a_3=\frac{|\boldsymbol{A}_3|}{\boldsymbol{A}}$

其中

$|\boldsymbol{A}_1|=\begin{vmatrix}\color{blue}{3}&1&1^2&1^3\\ \color{blue}{5}&2&2^2&2^3\\ \color{blue}{2}&4&4^2&4^3\\ \color{blue}{4}&5&5^2&5^3\end{vmatrix}=-432\quad |\boldsymbol{A}_2|=\begin{vmatrix}1&\color{blue}{3}&1^2&1^3\\ 1&\color{blue}{5}&2^2&2^3\\ 1&\color{blue}{2}&4^2&4^3\\ 1&\color{blue}{4}&5^2&5^3\end{vmatrix}=984$

$|\boldsymbol{A}_3|=\begin{vmatrix}1&1&\color{blue}{3}&1^3\\ 1&2&\color{blue}{5}&2^3\\ 1&4&\color{blue}{2}&4^3\\ 1&5&\color{blue}{4}&5^3\end{vmatrix}=-378\quad |\boldsymbol{A}_4|=\begin{vmatrix}1&1&1^2&\color{blue}{3}\\ 1&2&2^2&\color{blue}{5}\\ 1&4&4^2&\color{blue}{2}\\ 1&5&5^2&\color{blue}{4}\end{vmatrix}=42$

这样就可以计算出

$a_0=-6\quad a_1=\frac{41}{3}\quad a_2=-\frac{21}{4}\quad a_3=\frac{7}{12}$

(3)将 $a_0,a_1,a_2,a_3$ 的值带回多项式，可以得到曲线的表达式为

$y=-6+\frac{41}{3}x-\frac{21}{4}x^2+\frac{7}{12}x^3$

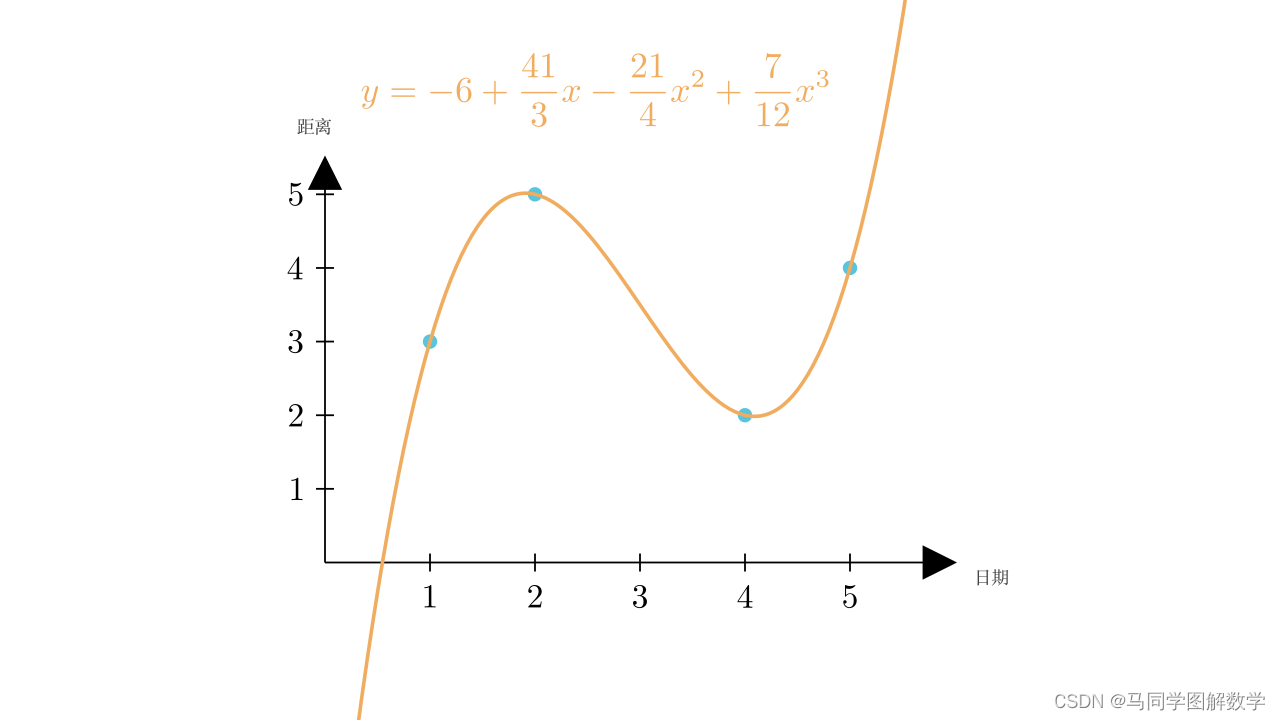
4 结论

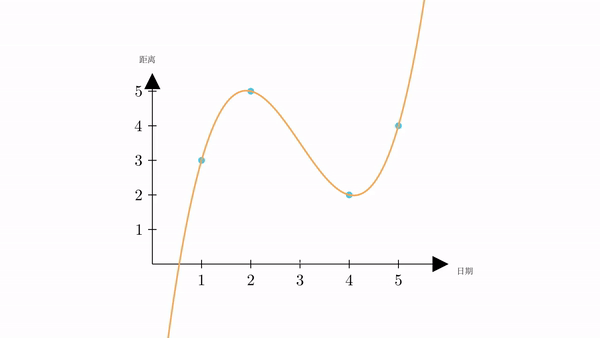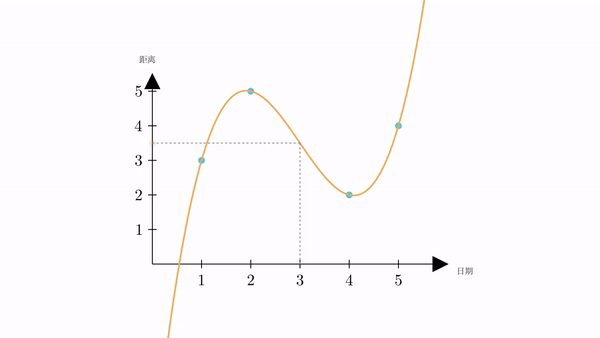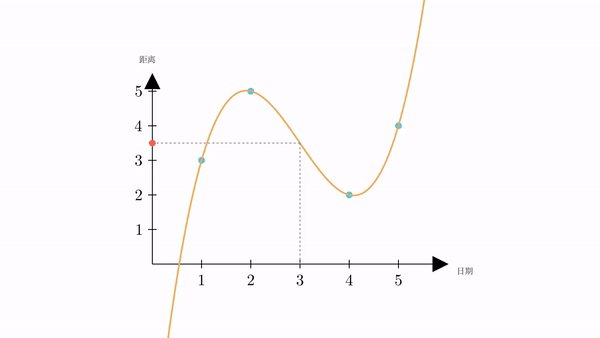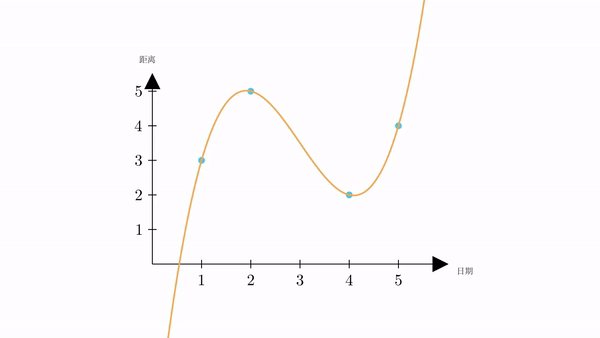
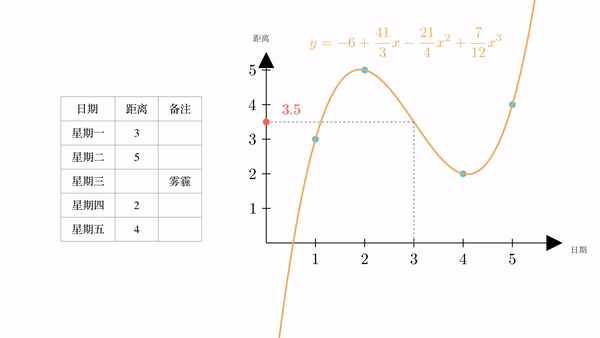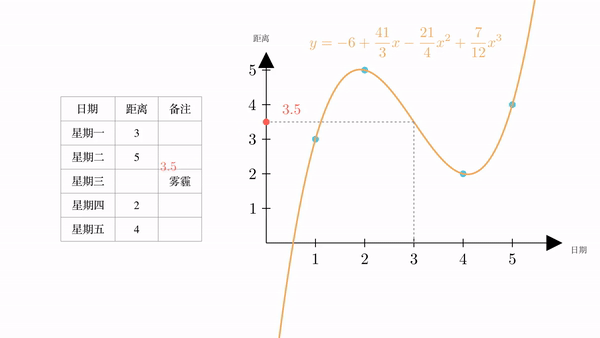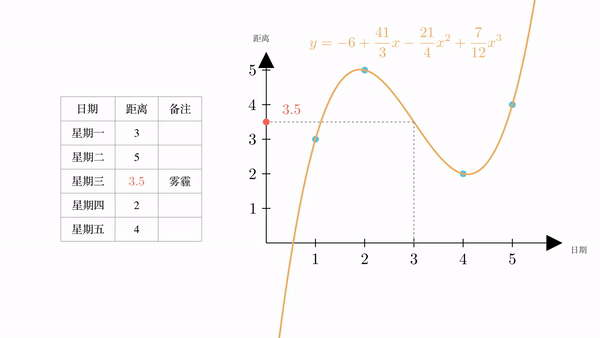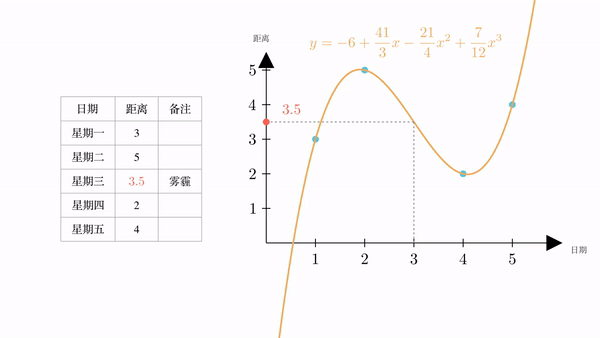
有了曲线的表达式，我们可以很容易的计算出，当 $x=3$ 时， $y=3.5$

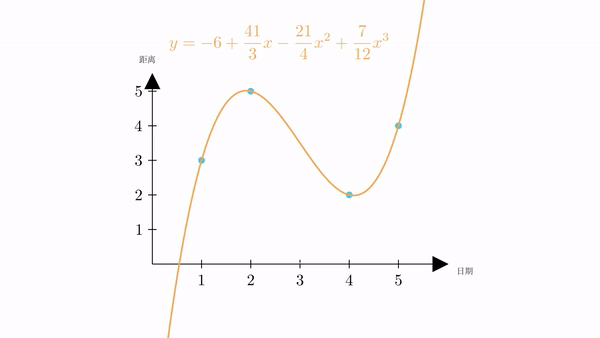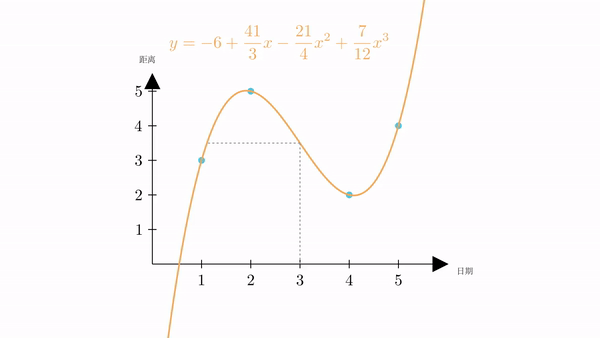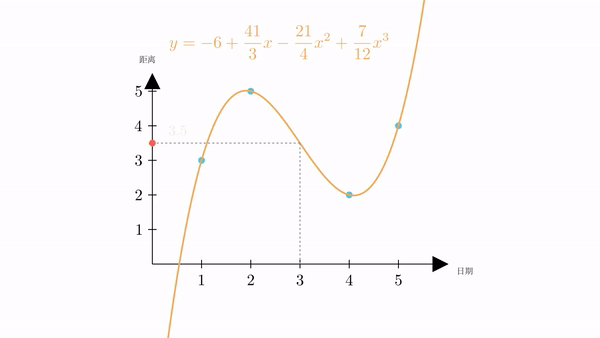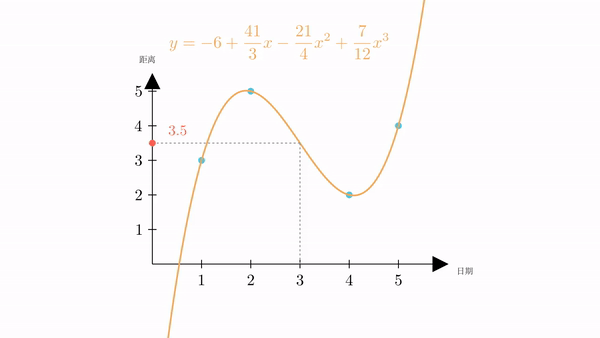
也就是说，根据插值，我们计算出星期三火星距离地球为3.5万公里

5 一点补充

插值的方法有很多，除了本文介绍方法外，还有牛顿插值法、拉格朗日插值法等。感兴趣的同学，可以在我们的微信公众号《马同学图解数学》中，回复相应关键字查看

您可能感兴趣的与本文相关的镜像

Anything-LLM

AI应用

AnythingLLM是一个全栈应用程序，可以使用商用或开源的LLM/嵌入器/语义向量数据库模型，帮助用户在本地或云端搭建个性化的聊天机器人系统，且无需复杂设置