(1)在由3×3个方格构成的方阵填入1~10中的9个数字,每个方格填一个整数,使得所有相邻两个方格内的整数之和为素数。请设计算法求出所有满足这个要求的数字填法。
#include<iostream>
using namespace std;
int maze[4][4]; //小方阵
int ans = 0;
int tag[11];
bool IsPrime(int x) //判断素数
{
for (int i = 2; i * i <= x; i++)
{
if (x % i == 0)
return false;
}
return true;
}
bool panduan(int x, int y, int t)
{
if (tag[t] == 1)
return false;
if (x - 1 >= 1)
{
if (!IsPrime(maze[x - 1][y] + t))
return false;
}
if (y - 1 >= 1)
{
if (!IsPrime(maze[x][y - 1] + t))
return false;
}
return true;
}
void dfs(int x, int y)
{
if (x == 4) //说明已经来到边界
{
ans++;
cout << "********" << endl;
for(int i = 1;i <= 3;i++)
{
for(int j = 1;j <= 3;j++)
{
cout << maze[i][j] << " ";
}
cout << endl;
}
return;
}
for (int i = 1; i <= 10; i++)
{
if (panduan(x, y, i))
{
tag[i] = 1;
maze[x][y] = i;
if (y != 3)
dfs(x, y + 1);
else
dfs(x + 1, 1);
maze[x][y] = 0;
tag[i] = 0;
}
}
}
int main()
{
dfs(1, 1);
cout << ans << endl;
return 0;
}
(2)设计一个算法求出满足方程ab-cd+e=1的变量a、b、c、d、e的值,其中所有变量的取值为1~5并且互不相同。
#include<iostream>
using namespace std;
int vis[6] = { 0 };
void f(int a[], int k, int n)
{
if (k == n)
{
if (a[0] * a[1] - a[2] *a[3] + a[4] == 1)
{
cout << a[0] << ' ' << a[1] << ' ' << a[2] << ' ' << a[3] << ' ' << a[4] << endl;
}
return;
}
for (int i = 1; i <= n; i++)
{
if (vis[i] == 0)
{
vis[i] = 1;
a[k] = i;
f(a, k + 1, n);
vis[i] = 0;
}
}
}
int main()
{
int a[6];
f(a, 0, 5);
return 0;
}
(3)设计一个算法,采用队列式和优先队列式分支限界法求解4皇后问题的一个解。
#include<iostream>
#include<vector>
#include<queue>
using namespace std;
int count = 1;
struct Node
{
int no;
int row;
vector<int>cols;
bool operator<(const Node& s)const
{
return row < s.row;
}
};
int isOK(vector<int> cols, int i, int j) //测试(i,j)这个结点能否放在棋盘上作为皇后
{
for (int k = 0; k < i; k++)
{
if ((cols[k] == j) || abs(cols[k] - j) == abs(k - i))
return 0;
}
return 1;
}
void queen()
{
int i, j, count = 1;
Node e, e1;
priority_queue<Node>qu;
e.no = count++;
e.row = -1;
qu.push(e);
while (!qu.empty())
{
e = qu.top();
qu.pop();
if (e.row == 3)
{
cout << "4皇后问题的一个解:" << endl;
for (i = 0; i < 4; i++)
cout << "[" << i + 1 << "," << e.cols[i] + 1 << "]" << endl;
return;
}
else
{
for (j = 0; j < 4; j++)
{
i = e.row + 1;
if (isOK(e.cols, i, j))
{
e1.no = count++;
e1.row = i;
e1.cols = e.cols;
e1.cols.push_back(j);
qu.push(e1);
}
}
}
}
}
int main()
{
queen();
return 0;
}
(4)世界上有超过100万种动物,各种动物有自己的语言。假设动物A可以直接与动物B进行交流,但无法直接与动物C交流,动物C只能直接与动物B交流,所以动物A、C之间的交流需要动物B来当翻译。给定动物数量和可以直接交流的动物种类,欲使所有动物之间都可以交流,至少需要多少个翻译?
#include <iostream>
using namespace std;
struct Node
{
int num;
int length;
};
struct Queue_node //队列的结点
{
Node item;
Queue_node* next;
};
struct Queue //表示一个队列,包含头指针和尾指针
{
Queue_node* front, * rear;
};
bool is_queue_empty(Queue* Q) //判断队列Q是否为空,如果是则返回true,否则返回false
{
if (Q->front == NULL || Q->rear == NULL)
return true;
else
return false;
}
void enQueue(Queue*& Q, Node item) //把item加到队列Q的队尾
{
Queue_node* p = new Queue_node;
p->item = item;
p->next = NULL;
if (is_queue_empty(Q))
{
Q->front = Q->rear = p;
Q->rear = p;
}
else
{
Q->rear->next = p;
Q->rear = p;
}
}
bool deQueue(Queue*& Q, Node& item) //移出队头元素,并将其赋给item
{
if (is_queue_empty(Q))
return false;
Queue_node* p = Q->front;
if (Q->front == Q->rear)
Q->front = Q->rear = NULL;
else
{
Q->front = Q->front->next;
}
item = p->item;
delete p;
return true;
}
void init_queue(Queue*& Q) //初始化队列Q
{
Q = new Queue;
Q->front = Q->rear = NULL;
}
int bfs(bool** graph, int n, int animal_1, int animal_2)
{
int best = 999; //记录目前所得到的最短路径长度
Queue* Q = NULL;
init_queue(Q);
Node e, item;
e.num = animal_1;
e.length = 0;
enQueue(Q, e);
while (!is_queue_empty(Q))
{
deQueue(Q, item);
if (item.length > best || (item.num != animal_2 && item.length == best))
continue;
else if (item.num == animal_2 && item.length < best)
{
best = item.length;
continue;
}
for (int i = 0; i < n; i++)
{
if (graph[item.num][i] == 1 && i != animal_1)
{
e.num = i;
e.length = item.length + 1;
enQueue(Q, e);
}
}
}
if (best == 0 || best == 1) //如果最短路径等于0或者1,则中间结点个数为0
return 0;
else if (best < 999) //其他情况的中间结点个数为最短路径减一
return best - 1;
else //无路径
return -1;
}
int main(void)
{
int n, m, k, animal_1, animal_2, result[20], a, b;
int i, j;
cin >> n >> m;
bool** graph = new bool* [n];
for (i = 0; i < n; i++)
{
graph[i] = new bool[n];
}
for (i; i < n; i++) //初始化二维数组graph
{
for (j = 0; j < n; j++)
{
graph[i][j] = 0;
}
}
for (i = 0; i < m; i++) //输入通信关系
{
cin >> animal_1 >> animal_2;
graph[animal_1][animal_2] = 1;
graph[animal_2][animal_1] = 1;
}
cin >> k;
for (i = 0; i < k; i++)
{
cin >> a >> b;
result[i] = bfs(graph, n, a, b);
}
for (i = 0; i < k; i++) //输出结果
cout << result[i] << endl;
return 0;
}
运行结果
(1)
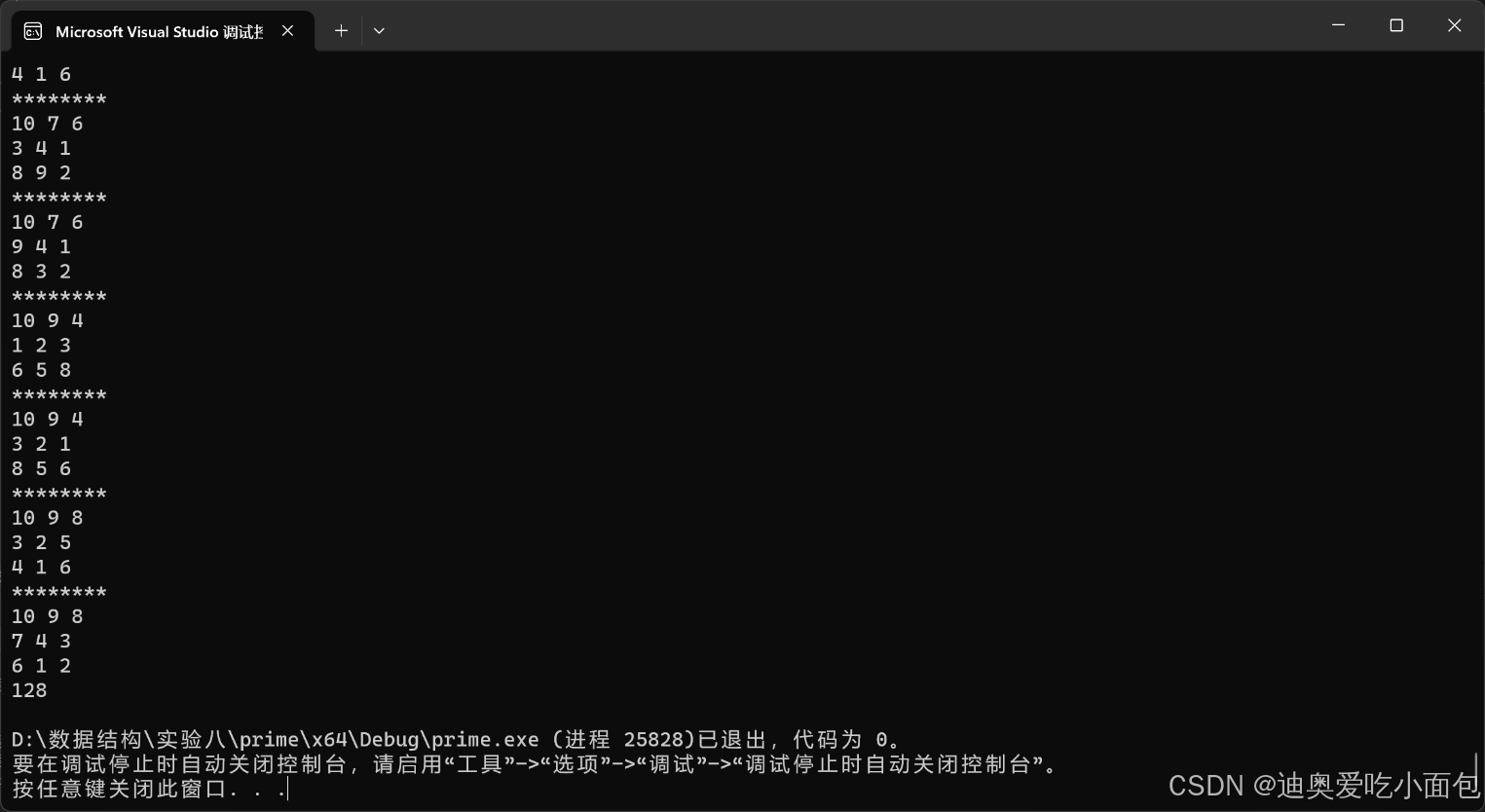
(2)
(3)
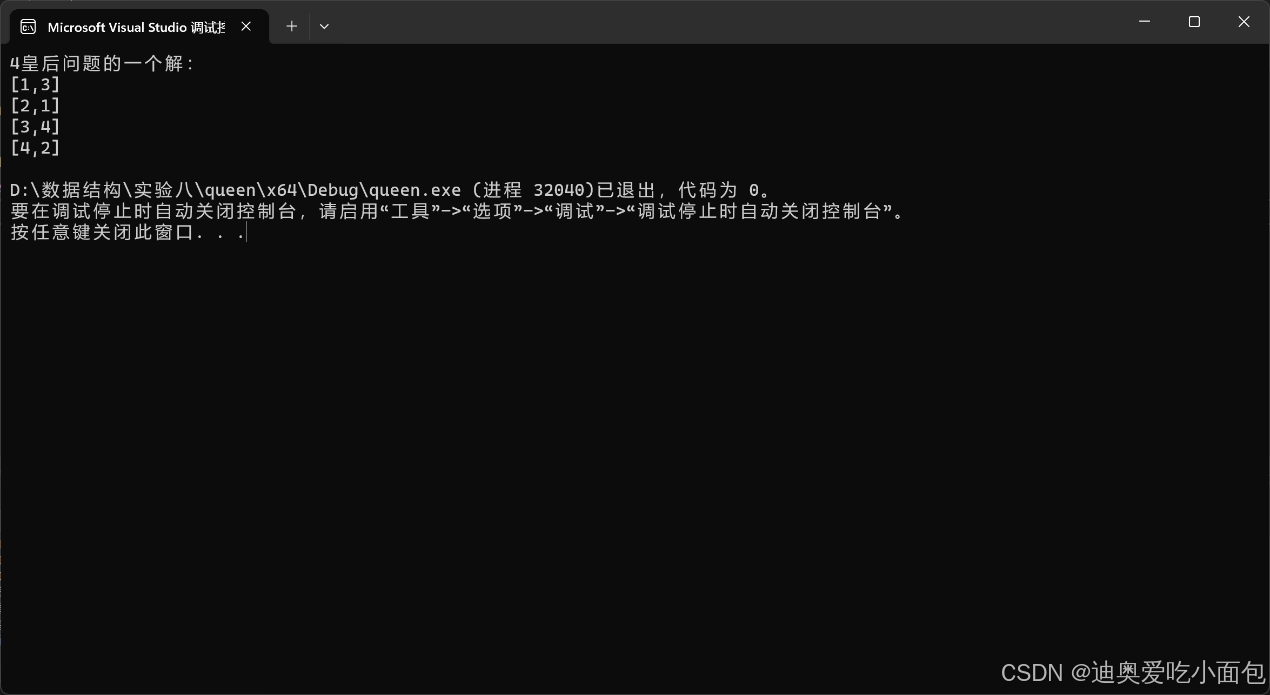
(4)
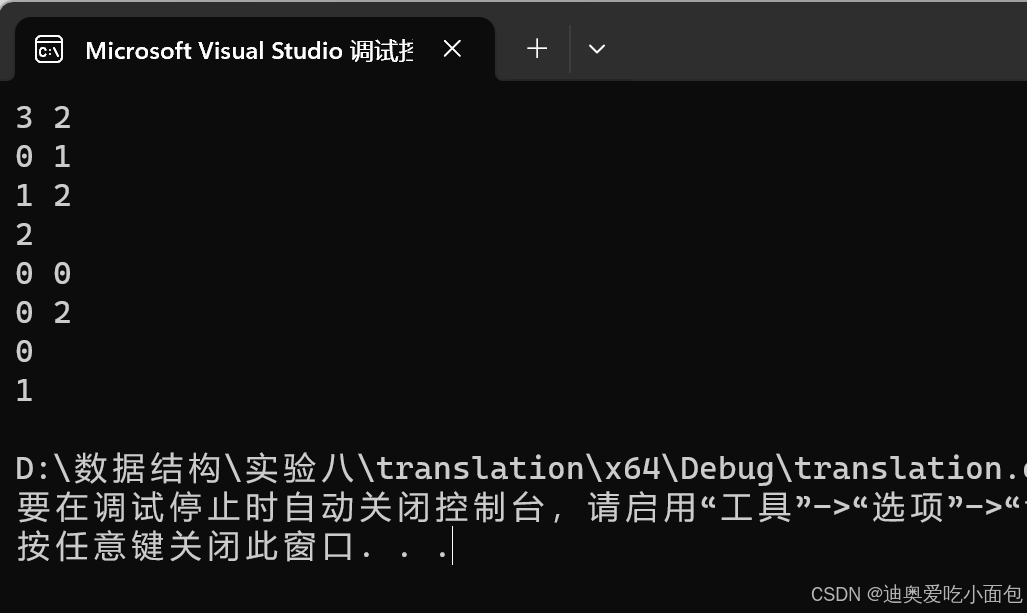




















 950
950

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








