循环链表II

OJ链接： 循环链接II

• 方法一：快慢指针

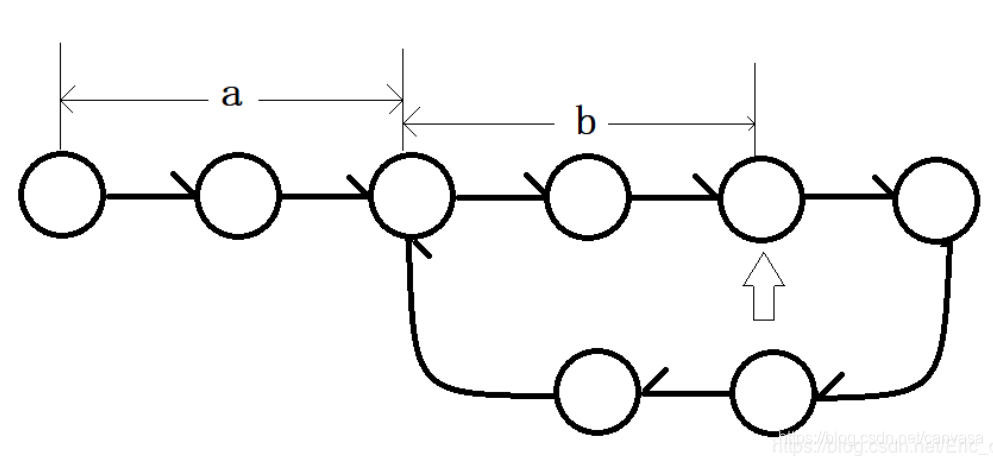
使用快慢指针，快指针每次走2步，慢指针每次走1步。当有环相遇时，说明快指针走过的路程是慢指针的两倍，假设链表头结点到环入口位置距离为a，环的入口与相遇节点位置距离为b，环的长度为R，我们计算快慢指针所走过的距离：

d(fast)=a+b+n*R, d(slow)=a+b。

快指针的速度是慢指针的两倍，相同时间，快指针所走过的路程应该是慢指针所走过路程的两倍，于是：d(fast)=2*d(slow)。

所以有：a=n*R-b。

当n = 1时，也就是快指针走了一圈之后，在第二圈的时候遇见了慢指针，a = R - b。

我们可以发现，a是链表的表头到环的入口点的位置，(R - b)是相遇点到环入口点的位置。

但是我们需要考虑一种特殊情况，链表是首尾相连的：

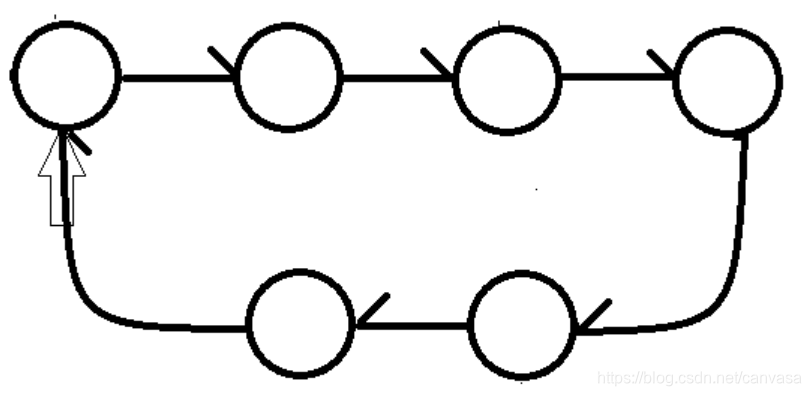
我们可以发现，如果链表的表头就是入口点，使用快慢指针的时候，因为快指针是慢指针的速度的2倍，所以它们一定是慢指针走了一圈，快指针走了两圈的时候相遇，就是在环的入口点相遇。 

代码

	ListNode *detectCycle(ListNode *head){
        ListNode *fast = head;
        ListNode *slow = head;
        while(fast != NULL && fast->next != NULL){//判断是否有环
            fast = fast->next->next;
            slow = slow->next;

            if(fast == slow) //有环，找到环入口
            {
                fast = head; //重新从开始找，每次一步，相遇是入口
                while(fast != slow){
                    fast = fast->next;
                    slow = slow->next;
                }
                return fast;
            }
        }
        return NULL;
    }

• 方法二：set

使用set来保存每一个链表中元素，在保存前先查看set中是否已经存在，若存在说明是环的入口地址，返回该节点即可，否则插入到set里。

代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        set<ListNode*> s;
        ListNode* cur=head;

        while(cur)
        {
            if(s.find(cur)!=s.end())
                return cur;

            else
            {
                s.insert(cur);
                cur=cur->next;
            }
        }
        return NULL;
    }
};