蓝桥杯之“递归三元组”回溯解法，含图解(Java)

题目描述
给定三个整数数组
A = [A1, A2, … AN],
B = [B1, B2, … BN],
C = [C1, C2, … CN]，
请你统计有多少个三元组(i, j, k) 满足：

1 <= i, j, k <= N
Ai < Bj < Ck
【输入格式】
第一行包含一个整数N。
第二行包含N个整数A1, A2, … AN。
第三行包含N个整数B1, B2, … BN。
第四行包含N个整数C1, C2, … CN。

对于30%的数据，1 <= N <= 100
对于60%的数据，1 <= N <= 1000
对于100%的数据，1 <= N <= 100000 0 <= Ai, Bi, Ci <= 100000

【输出格式】
一个整数表示答案

【输入样例】
3
1 1 1
2 2 2
3 3 3

【输出样例】
27
 

解题思路：

1、定义一个3行n列的二维数组，并给每一行的数据排序，排序的目的是为后面减少计算量

2、根据题意，我们需要拿出每一行中的数字组成递增数列。这时可以利用回溯算法，对数列进行排序组合。

3、回溯利用深度优先算法，当遍历到叶子结点时，返回上一层。   

完整代码如下：

import java.util.Scanner;
import java.util.Arrays;
// 1:无需package
// 2: 类名必须Main, 不可修改

public class Main {
    public static int result = 0;
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        int n = scan.nextInt();
        int[][] quare = new int[3][n];
        for(int i = 0; i < 3; i++){
            for(int k = 0; k < n; k++){
                quare[i][k] = scan.nextInt();
            }
            Arrays.sort(quare[i]);
        }
        //调用回溯函数
        dfs(quare,n,0,quare[0][0],0);
        System.out.println(result);
        scan.close();
    }

    public static void dfs(int[][] quare, int n, int start, int pre, int index){
        if(start == 3){
            result = result + (n - index);
            return;
        }
        for(int i = 0; i < n; i++){
            if(start > 0){
                if(quare[start][i] > pre){
                    dfs(quare,n,start+1,quare[start][i],i);
                    if(start == 2) break;
                }
            }else{
                dfs(quare,n,start+1,quare[start][i],i);
            }
        }
    }
}

start表示当前访问数列的下标,

pre代表上一个数列中的元素，如当前元素大于上一个数列元素时进行递归操作。

index代表访问当前元素在数列中的位置（即下标）

算法图解：演示回溯算法的前四步 

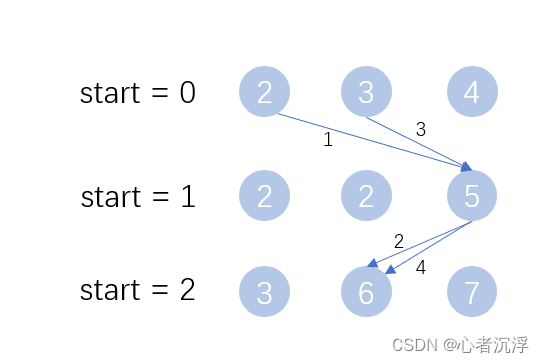
另外，非递归的方法提供给大家参考：

import java.util.Scanner;
import java.util.Arrays;
public class Main{
    public static int result = 0;
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        int n = scan.nextInt();
        int[][] quare = new int[3][n];
        for(int i = 0; i < 3; i++){
            for(int k = 0; k < n; k++){
                quare[i][k] = scan.nextInt();
            }
            //排序
            Arrays.sort(quare[i]);
        }
        for(int i = 0; i < n; i++){
            for(int m = 0; m < n; m++){
                if(quare[1][m] > quare[0][i]){
                    for(int k = 0; k < n; k++){
                        if (quare[2][k] > quare[1][m]){
                            result += (n - k);
                            break;
                        }
                    }
                }

            }
        }
        System.out.println(result);
        scan.close();
    }
}