思路:像素变化大的地方可能是角点,所以,像素变化函数E(u,v),即通过窗口移动得到的,该函数的泰勒展开得到的形式转化为矩阵表达,分析矩阵即可以看出灰度变化—通过该矩阵的特征值可以看出,**如果两个特征值都大,说明有较明显的灰度变化,则是角点;如果一个大一个小,则是边缘;如果都比较小,则不是角点。**特征值可以通过行列式的值和迹来表示,矩阵的迹:等于所有特征值的和,行列式等于特征值的乘积。
基本思想:以某一个点为中心的小窗口移动,小窗口任意方向移动,如果窗口内灰度剧烈变化,则是角点;如果是窗口单方向移动时变化,则是边缘。
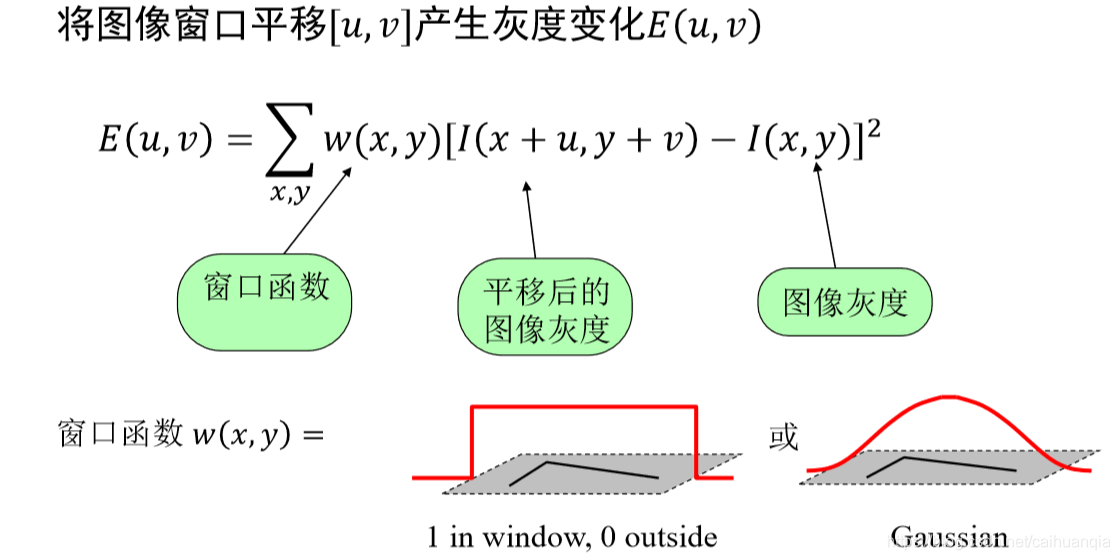
泰勒展开和矩阵表达:
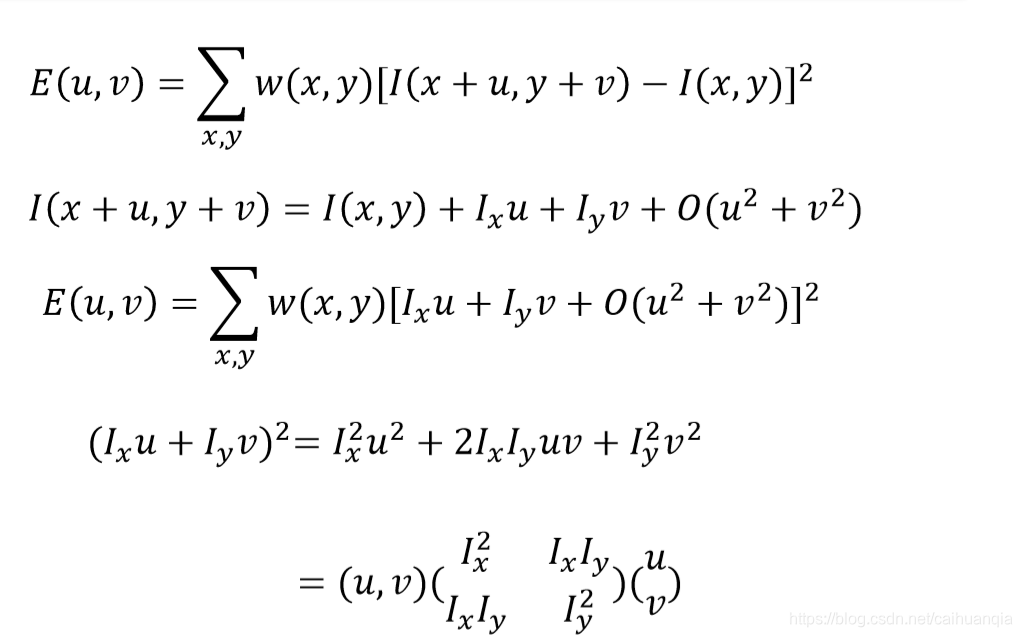

转化为对特征值的分析
实对称矩阵M的变化可以反映在特征值上!!!!

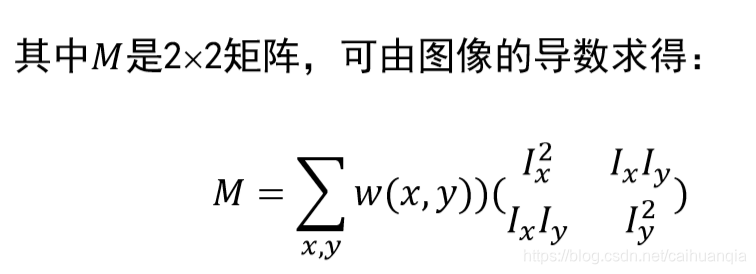
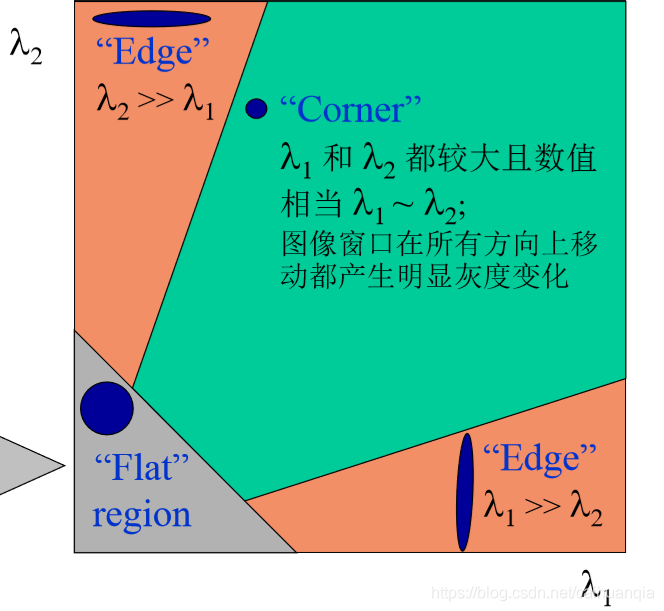
一旦两个特征值都比较大,则变化大;如果一个大一个小,则是边缘;如果都比较小,则不是角点。
方阵的迹:方阵对角元素的和。
矩阵的迹:等于所有特征值的和
行列式等于特征值的 乘积
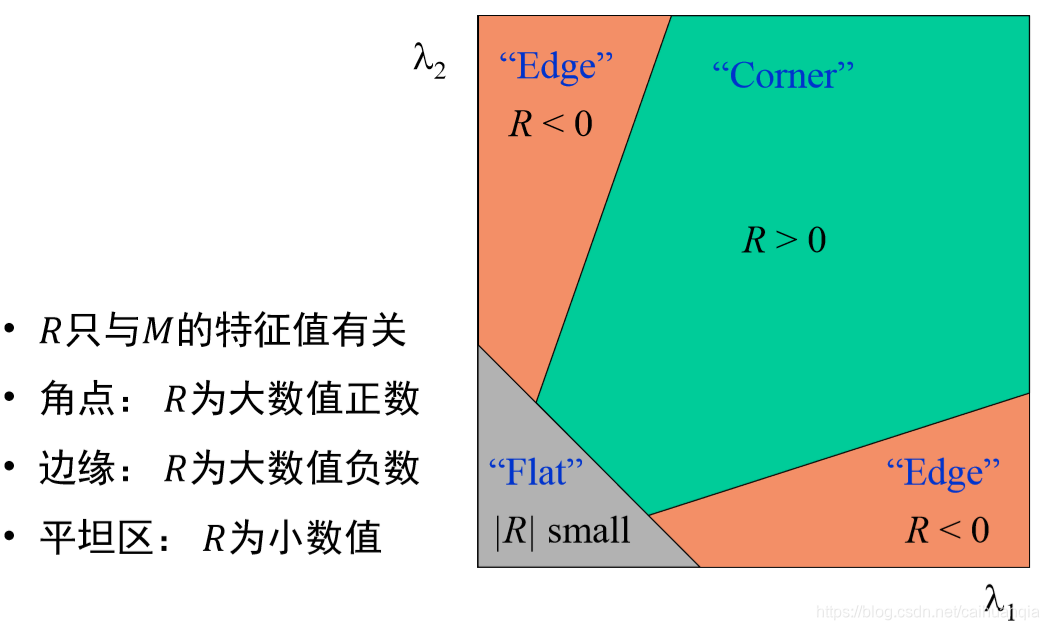
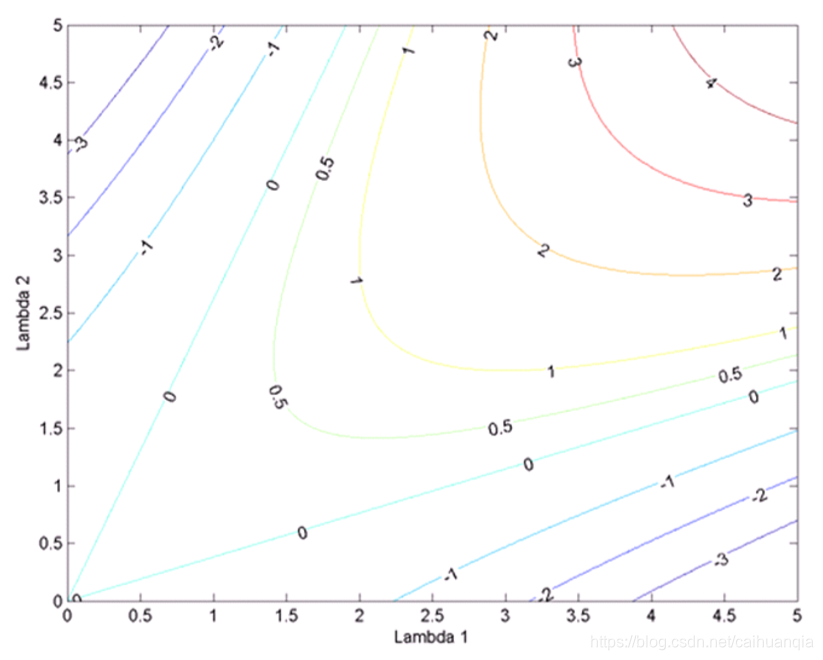
转化为响应函数分析

R接近0是平坦区域、R是负数是边缘、R较大是焦点
算法
对焦点响应函数进行阈值处理,大于阈值则是角点。
对每一个像素进行操作,都计算其梯度得到M矩阵,计算对应的响应函数的值,再与阈值进行判断。
角点性质
角点响应函数R对于图像的旋转具有不变性。(特征值保持不变)
灰度仿射变化具有部分不变性。包括平移(灰度的加性变化) 和 尺度变化(乘性解决不了)-大的更大了
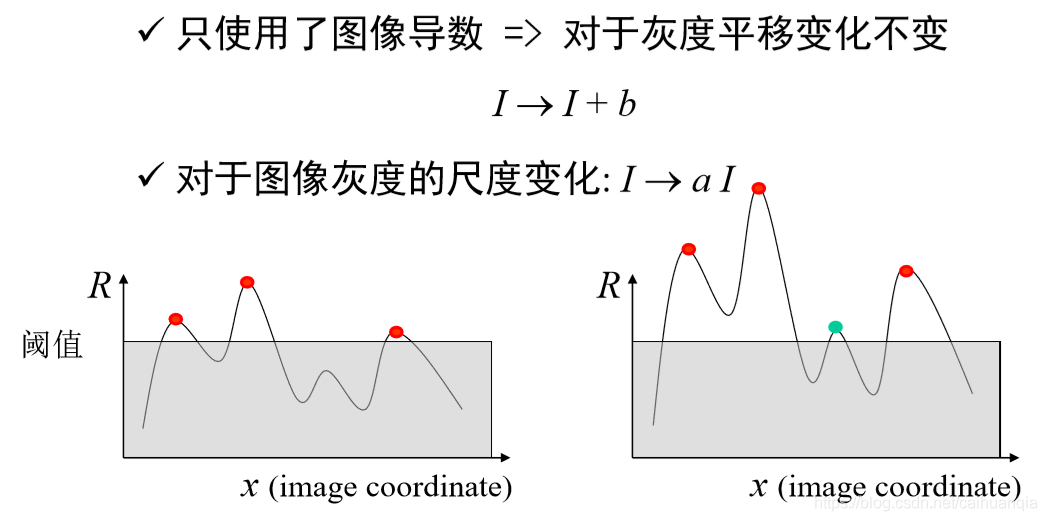
对于几何尺度变化不具有不变性。(从100米看和从1米看)
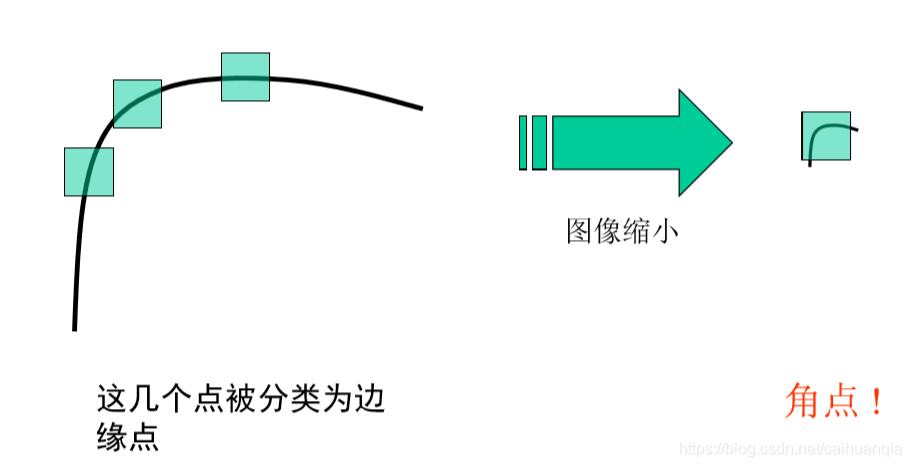





 本文深入探讨了角点检测的基本思想,通过分析像素变化函数E(u,v)的泰勒展开和矩阵表达,揭示了角点、边缘和平坦区域的特征值区别。详细解释了响应函数R如何用于区分不同类型的图像特征,并介绍了角点检测算法的实现步骤。
本文深入探讨了角点检测的基本思想,通过分析像素变化函数E(u,v)的泰勒展开和矩阵表达,揭示了角点、边缘和平坦区域的特征值区别。详细解释了响应函数R如何用于区分不同类型的图像特征,并介绍了角点检测算法的实现步骤。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








