一、决策树(ID3算法)
1. 决策树的基本认识
决策树是一种依托决策而建立起来的一种树。在机器学习中,决策树是一种预测模型,代表的是一种对象属性与对象值之间的一种映射关系,每一个节点代表某个对象,树中的每一个分叉路径代表某个可能的属性值,而每一个叶子节点则对应从根节点到该叶子节点所经历的路径所表示的对象的值。决策树仅有单一输出,如果有多个输出,可以分别建立独立的决策树以处理不同的输出。接下来讲解ID3算法。
2. ID3算法介绍
ID3算法是决策树的一种,它是基于奥卡姆剃刀原理的,即用尽量用较少的东西做更多的事。ID3算法,即Iterative Dichotomiser 3,迭代二叉树3代,是Ross Quinlan发明的一种决策树算法,这个算法的基础就是上面提到的奥卡姆剃刀原理,越是小型的决策树越优于大的决策树,尽管如此,也不总是生成最小的树型结构,而是一个启发式算法。
在信息论中,期望信息越小,那么信息增益就越大,从而纯度就越高。ID3算法的核心思想就是以信息增益来度量属性的选择,选择分裂后信息增益最大的属性进行分裂。该算法采用自顶向下的贪婪搜索遍历可能的决策空间。
3. 信息熵与信息增益
在信息增益中,重要性的衡量标准就是看特征能够为分类系统带来多少信息,带来的信息越多,该特征越重要。在认识信息增益之前,先来看看信息熵的定义
熵这个概念最早起源于物理学,在物理学中是用来度量一个热力学系统的无序程度,而在信息学里面,熵是对不确定性的度量。在1948年,香农引入了信息熵,将其定义为离散随机事件出现的概率,一个系统越是有序,信息熵就越低,反之一个系统越是混乱,它的信息熵就越高。所以信息熵可以被认为是系统有序化程度的一个度量。
假如一个随机变量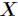 的取值为
的取值为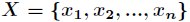 ,每一种取到的概率分别是
,每一种取到的概率分别是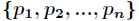 ,那么
,那么
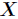 的熵定义为
的熵定义为
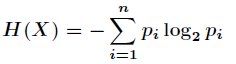
意思是一个变量的变化情况可能越多,那么它携带的信息量就越大。
对于分类系统来说,类别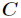 是变量,它的取值是
是变量,它的取值是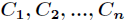 ,而每一个类别出现的概率分别是
,而每一个类别出现的概率分别是
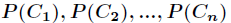
而这里的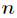 就是类别的总数,此时分类系统的熵就可以表示为
就是类别的总数,此时分类系统的熵就可以表示为
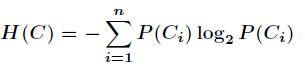
以上就是信息熵的定义,接下来介绍信息增益。
信息增益是针对一个一个特征而言的,就是看一个特征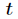 ,系统有它和没有它时的信息量各是多少,两者
,系统有它和没有它时的信息量各是多少,两者
的差值就是这个特征给系统带来的信息量,即信息增益。
接下来以天气预报的例子来说明。下面是描述天气数据表,学习目标是play或者not play。
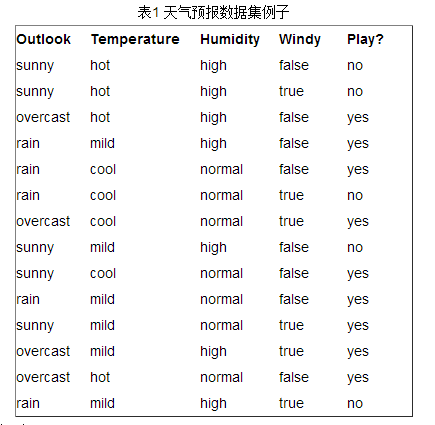
可以看出,一共14个样例,包括9个正例和5个负例。那么当前信息的熵计算如下
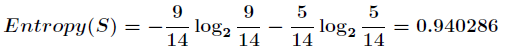
在决策树分类问题中,信息增益就是决策树在进行属性选择划分前和划分后信息的差值。假设利用
属性Outlook来分类,那么如下图
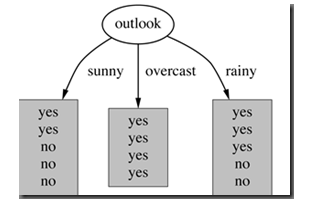
划分后,数据被分为三部分了,那么各个分支的信息熵计算如下
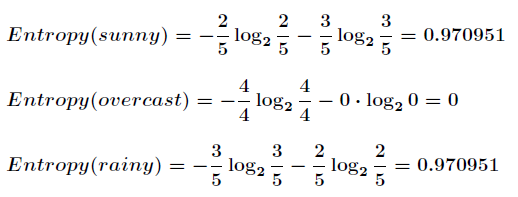
那么划分后的信息熵为
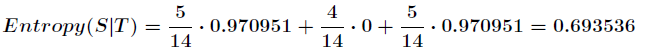
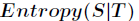 代表在特征属性
代表在特征属性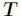 的条件下样本的条件熵。那么最终得到特征属性
的条件下样本的条件熵。那么最终得到特征属性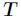 带来的信息增益为
带来的信息增益为
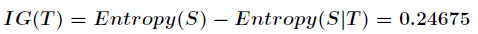
信息增益的计算公式如下
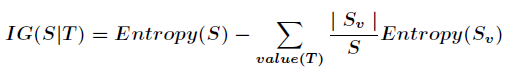
其中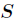 为全部样本集合,
为全部样本集合,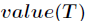 是属性
是属性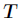 所有取值的集合,
所有取值的集合,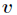 是
是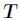 的其中一个属性值,
的其中一个属性值,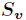 是
是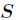 中属性
中属性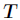 的
的
值为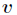 的样例集合,
的样例集合,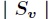 为
为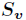 中所含样例数。
中所含样例数。
在决策树的每一个非叶子结点划分之前,先计算每一个属性所带来的信息增益,选择最大信息增益的属性来划
分,因为信息增益越大,区分样本的能力就越强,越具有代表性,很显然这是一种自顶向下的贪心策略。以上
就是ID3算法的核心思想。
决策树停止的条件
如果发生以下的情况,决策树将停止分割
1.改群数据的每一笔数据已经归类到每一类数据中,即数据已经不能继续在分。
2.该群数据已经找不到新的属性进行节点分割
3.该群数据没有任何未处理的数据
二、Python代码实现:
# The algorithm of ID3
import copy
import math
from math import log
from numpy import log2
def infoEntroy(dataset):
num = 0
for item in dataset:
num += item[0]
print("The number of dataset is %d " % num)
typeCounts = {}
for featvec in dataset:
currentType = featvec[-1]
if currentType not in typeCounts:
typeCounts[currentType] = featvec[0]
else:
typeCounts[currentType] += featvec[0]
entroy = 0.0
for key in typeCounts:
p = typeCounts[key] / num
entroy += - (p * math.log(p))
print(typeCounts)
return entroy
def optBestFeature(dataset):
d = copy.deepcopy(dataset)
m = len(dataset)
index = -1
minEntroy = infoEntroy(dataset)
print(minEntroy)
print()
for i in range(1, len(dataset[0]) - 1):
print("The No.%d feature:" % i)
typeCounts = []
for feature in d: # 获取该特征的所有特征值
if feature[i] not in typeCounts:
typeCounts.append(feature[i])
entroy = 0.0
for featVal in typeCounts: # 根据不同的特征值进行划分
count = 0
data = []
for item in d:
if item[i] == featVal:
data.append(item) # 將特征一样的元组放到同一个数据表中
count += 1
print(len(data))
entroy += count / m * infoEntroy(data) # 计算划分之后的信息熵
if entroy <= minEntroy:
minEntroy = entroy # 选取划分后得到的信息熵是最小的那个特征
index = i
print(entroy)
print()
return index
def createTree(dataset, deci_tree, features):
print(dataset)
if len(dataset) <= 2:
return deci_tree
else:
simple = dataset[0]
flag = True
for item in dataset:
for i in range(1, len(simple)-1):
if simple[i] != item[i]:
flag = False
break
if not flag:
break
if flag:
return deci_tree
typeCoutns = []
for item in dataset:
if item[-1] not in typeCoutns:
typeCoutns.append(item[-1])
print('typeCoutns{}'.format(typeCoutns))
print()
if len(typeCoutns) == 1:
return deci_tree
sign = optBestFeature(dataset)
featureCounts = []
for item in dataset:
if item[sign] not in featureCounts:
featureCounts.append(item[sign])
data = copy.deepcopy(dataset)
ID3tree = {}
for featVal in featureCounts:
feature = features
childData = []
for item in data:
if item[sign] == featVal:
simple = item[:]
del simple[sign]
childData.append(simple)
print('the No.{} featVal:{}'.format(sign, featVal))
print(childData)
classCounts = []
for item in childData:
if item[-1] not in classCounts:
classCounts.append(item[-1])
feature += str(featVal)
if feature not in ID3tree:
if len(classCounts) == 1:
ID3tree[feature] = classCounts[0]
elif len(classCounts) > 1:
ID3tree[feature] = -1
print(feature)
print(ID3tree)
print()
ID3tree = createTree(childData, ID3tree, feature)
deci_tree.update(ID3tree)
return deci_tree
if __name__ == '__main__':
# The dataset is number, stage of age, level of income ,is student or not, credit rating and final decision
# data = [
# (64, "young", "high", "no", "good", "N"),
# (64, "young", "high", "no", "great", "N"),
# (128, "midlife", "high", "no", "good", "Y"),
# (60, "old", "middle", "no", "good", "Y"),
# (64, "old", "low", "yes", "good", "Y"),
# (64, "old", "low", "yes", "great", "N"),
# (64, "midlife", "low", "yes", "great", "Y"),
# (128, "young", "middle", "no", "good", "N"),
# (64, "young", "low", "yes", "good", "Y"),
# (132, "old", "middle", "yes", "good", "Y"),
# (64, "young", "middle", "yes", "great", "Y"),
# (32, "midlife", "middle", "no", "great", "Y"),
# (32, "midlife", "high", "yes", "good", "Y"),
# (63, "old", "middle", "no", "great", "N"),
# (1, "old", "middle", "no", "great", "Y"),
# ]
data = [
[64, 0, 2, 0, 0, 0],
[64, 0, 2, 0, 1, 0],
[128, 1, 2, 0, 0, 1],
[60, 2, 1, 0, 0, 1],
[64, 2, 0, 1, 0, 1],
[64, 2, 0, 1, 1, 0],
[64, 1, 0, 1, 1, 1],
[128, 0, 1, 0, 0, 0],
[64, 0, 0, 1, 0, 1],
[132, 2, 1, 1, 0, 1],
[64, 0, 1, 1, 1, 1],
[32, 1, 1, 0, 1, 1],
[32, 1, 2, 1, 0, 1],
[63, 2, 1, 0, 1, 0],
[1, 2, 1, 0, 1, 1],
]
tree = {}
tree = createTree(data, tree, "")
print(tree)





 本文介绍了决策树中的ID3算法,这是一种基于信息增益选择属性进行划分的机器学习模型。ID3算法利用信息熵来度量数据的不确定性,并通过信息增益选择最佳属性进行分裂,以构建最小的决策树。文章还提供了Python代码示例,展示了如何实现ID3算法。
本文介绍了决策树中的ID3算法,这是一种基于信息增益选择属性进行划分的机器学习模型。ID3算法利用信息熵来度量数据的不确定性,并通过信息增益选择最佳属性进行分裂,以构建最小的决策树。文章还提供了Python代码示例,展示了如何实现ID3算法。

















 4867
4867

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










