树状数组有图理解

整理自《挑战程序设计竞赛（第二版）》

---

问题导学

给定一个数组a，如果要大量进行如下两个操作
给定 i ，求计算a1 + a2 + … + an
给定 i 和 x ，执行ai += x

如果用普通的方法第一个操作的复杂度为O(n)，第二个操作为O(1)

但如果数据量是千万级呢，在程序设计竞赛中，动态的计算结果显然会超时

这时候就引入了树状数组的概念

树状数组可以说是低配版线段树，他可以完成的功能线段树一样可以完成，不过树状数组比较容易构造

假设有个数组

int[] a = {5, 3, 7, 9, 6, 4, 1, 2};

用树来表示

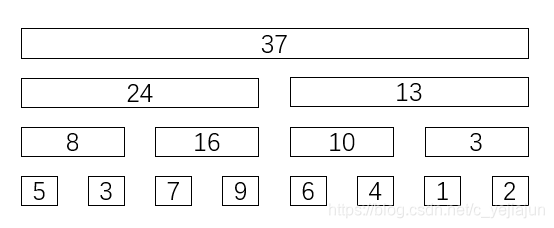
如果是求前7项和

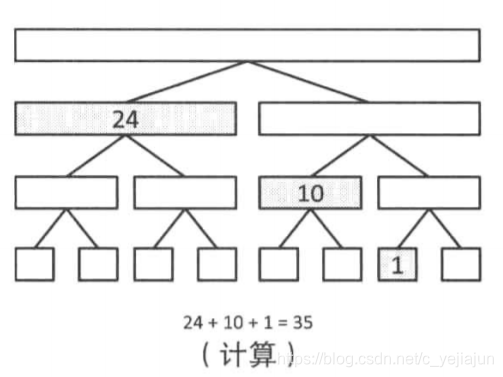
将第一个数加上-3

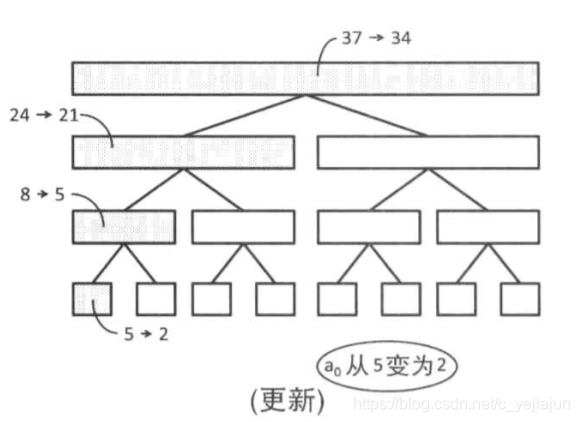
可以发现，无论是求和，还是更新操作，都与右儿子无关

这时我们把右儿子去掉

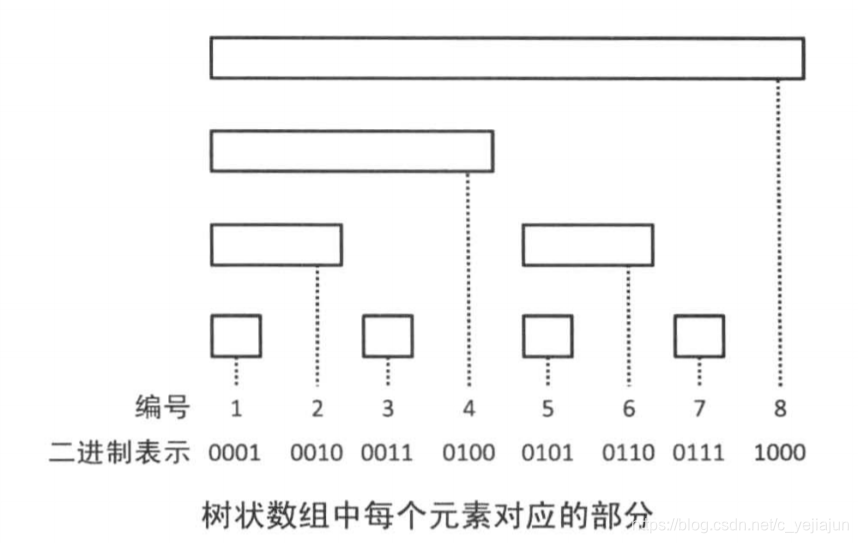
计算前 i 项和从 i 开始，不断减去 i 的二进制最低非0位对应的幂，直到 i 变成0，并累加结果

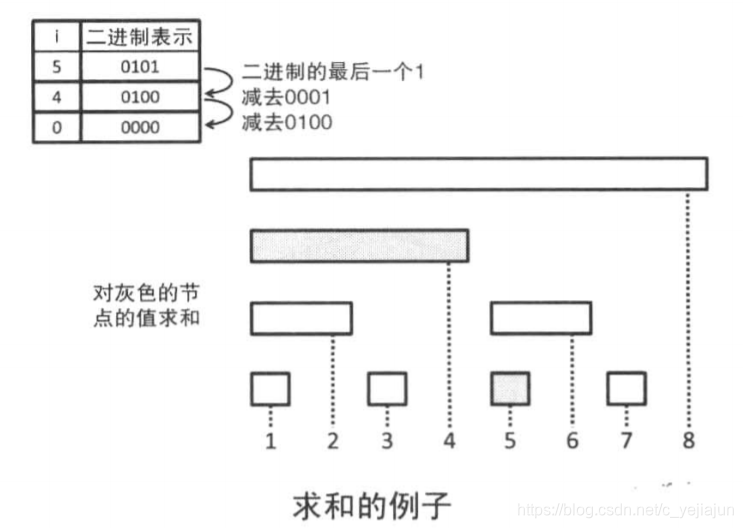
这里求前5项的和，只需加上第5项和第4项即可，可以发现每次需要加的下标都是减去二进制最后一个1之后的下标，直到0为止

而二进制最后一个1可以通过 i & -i 得到

同理，更新的例子也是

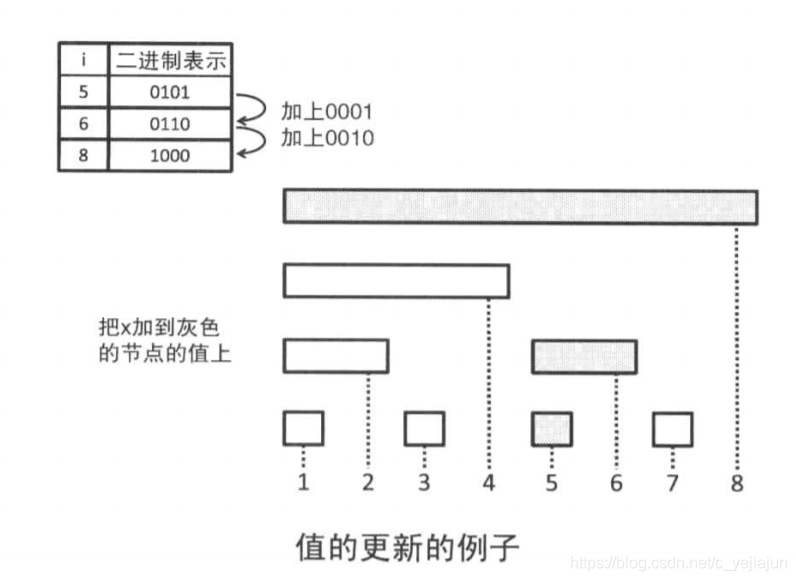
回到第一个问题，无论求和还是更新，复杂度都是O(logn)，可以满足需求

static int[] bit= new int[10000];  //程序需要多大就开多大

public static int sum(int i){
	int res = 0;
	while(i > 0){
		res += bit[i];
		i -= i & -i;
	}
	return res;
}

public static void add(int i, int x){
	while(i <= bit.length){
		bit[i] += x;
		i += i & -i;
	}
}