HDU - 6601 2019 Multi-University Training Contest 2（关于斐波那契有趣的性质）

最新推荐文章于 2020-07-22 17:32:16 发布

原创最新推荐文章于 2020-07-22 17:32:16 发布 · 145 阅读

0 ·

CC 4.0 BY-SA版权

线段树专栏收录该内容

20 篇文章

订阅专栏

本文介绍了一种使用线段树数据结构解决区间内最大三角形周长查询问题的方法。通过维护区间前50大的边长，并利用斐波那契数列特性判断是否能构成三角形，最终实现高效查询。

Keen On Everything But Triangle

在这里插入图片描述
simple input

simple output

13
16
16

题目大意：
N个数，这些数是三角形的边长，Q次查询，每次查询一个区间，问查询的区间里面构成最大三角形的周长是多少，如果区间里面的边不能构成三角形，那就输出-1

分析：
1e5次的查询，大家可能会想到线段树的查询，但是线段树需要去维护谁呢，这是个问题，维护最大值吗，这样的话递推到树顶的话不一定就是最大值，那要怎么处理呢，大家看下面这个程序：

int a[100]={0,1,1,2,3};
    for(int i=5;i<=50;i++){
        a[i]=a[i-1]+a[i-2];
        cout<<i<<" "<<a[i]<<endl;
    }

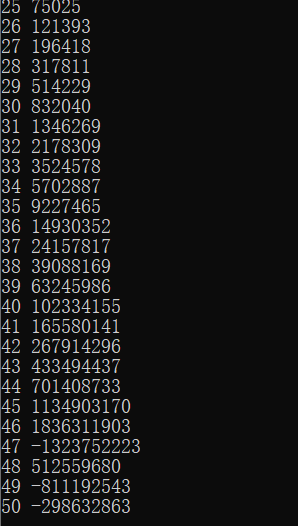
在这里插入图片描述
没错，这就是斐波那契数列，因为题目中说明了变成是1e9之内的，也就是说都是在int范围内的，那么就可以说明，如果边长的个数超过了47的话，就是一定能构成三角形的，因为菲波那切数列是刚好后一项是前两项的和，那么这样的话就可以给出我们一个思路了：
线段树只需要维护一个区间的前50个大的边就好了

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<string>
#include<cmath>
#include<cstring>
#include<set>
#include<queue>
#include<stack>
#include<map>
typedef long long ll;
using namespace std;
const int N=4e5+100;
struct node{
    int l,r,cnt;
    ll maxv[55];//区间的前50个大的变边
}num[N];
ll a[510],res[510];
int tot;
void push_up(int x){
    int i=0,j=0;
    for(int k=0;k<50;k++){

        if(num[x<<1].maxv[i]>num[x<<1|1].maxv[j])
            num[x].maxv[k]=num[x<<1].maxv[i],i++;
        else
            num[x].maxv[k]=num[x<<1|1].maxv[j],j++;
    }
}
void build(int id,int l,int r){
    num[id].l=l,num[id].r=r;
    if(l==r){
        for(int i=0;i<50;i++)
        num[id].maxv[i]=0;

        scanf("%lld",&num[id].maxv[0]);
        num[id].cnt=1;
        return ;
    }
    int mid=(l+r)/2;
    build(id<<1,l,mid);
    build(id<<1|1,mid+1,r);
    push_up(id);
}

void query(int id,int l,int r){

    if(l==num[id].l&&num[id].r==r){

    for(int i=0;i<50;i++)
        res[i]=a[i];
    int i=0,j=0;
    for(int k=0;k<50;k++){
        if(num[id].maxv[i]>res[j])
            a[k]=num[id].maxv[i],i++;
        else
            a[k]=res[j],j++;
      }
        return;
    }
    int mid=(num[id].l+num[id].r)/2;
    if(mid>=r) query(id<<1,l,r) ;
    else if(mid<l) query(id<<1|1,l,r);
    else{
        query(id<<1,l,mid);
        query(id<<1|1,mid+1,r);
    }
}
ll solve(int l,int r){
    query(1,l,r);
    sort(a,a+50,greater<ll>());

    for(int i=0;i<48;i++)
        if(a[i]<a[i+1]+a[i+2])
        return a[i]+a[i+1]+a[i+2];
    return -1;
}
int main()
{
    #ifndef ONLINE_JUDGE
    freopen("in.txt","r",stdin);
    #endif // ONLINE_JUDGE
    int n,q;
    while(scanf("%d%d",&n,&q)!=EOF){
        build(1,1,n);
        int l,r;
        for(int i=0;i<q;i++){
        scanf("%d%d",&l,&r);
        for(int i=0;i<300;i++) a[i]=0;

        printf("%lld\n",solve(l,r));
        }
    }
    return 0;
}