LTE-A网络干扰建模

国际电信联盟‐无线电通信部门兼容的 LTE‐Advanced网络站点间和扇区间干扰模型

摘要

在LTE‐Advanced网络中，每站点三个扇区且频率复用因子为1的蜂窝网络部署是支持高速数据应用的关键。然而，此类配置会导致小区间干扰增加。本文针对两个载波频率，对LTE‐Advanced网络中的小区间干扰影响进行了建模。我们考虑了两种城市环境和四种小区范围。小区间干扰的影响被分解为站点间干扰和扇区间干扰两部分。采用特定站点的三维射线追踪工具对基站（服务链路和干扰链路）与用户设备终端之间的通信信道进行建模。首先，将站点间干扰以主导干扰比例的形式进行建模，并利用先前在伦敦（英国）记录的实地测量数据进行验证。其次，将站点间干扰和扇区间干扰分量建模为用户设备相对于服务基站的相对位置的函数。我们的方法与标准化的国际电信联盟无线电通信模型兼容，所提出的模型可轻松集成到这些国际模型中。该模型无需干扰源的系统布局信息，与系统布局方法相比，所需信道生成时间减少了12倍。

索引术语

第四代移动通信，小区间干扰，干扰建模，射线追踪信道模型。

一、引言

第四代（4G）及以后的无线接口技术，例如第三代合作伙伴计划（3GPP）LTE‐Advanced标准，目标是每个基站（BS）站点部署三个扇区，并采用频率复用因子为一。这能够高效利用授权频谱，并具备实现高系统容量的潜力。在这种部署中，由于站间干扰（ISI）和扇区间干扰（IsecI），预计小区间干扰（ICI）将显著增加。此处，ISI指的是来自不同站点的干扰信号的总和围绕服务基站站点的第一层六个站点间干扰基站站点的不同扇区，而IsecI是站点内干扰，表示来自同一服务基站站点内另外两个扇区的干扰信号之和。ISI和IsecI的影响会降低用户设备（UE）接收到的信干噪比（SINR），并对系统性能产生负面影响，尤其是在小区边缘。根据[1]，当频率复用因子从三减少到一时，可预期出现10 dB SINR下降。

小区间干扰是第四代移动通信及蜂窝网络以上面临的一个关键问题[3]。因此，对用户设备（UE）处的干扰信号电平进行精确建模，对于干扰缓解和消除方案的有效系统设计和系统级评估至关重要[4]。现有文献中存在多项研究针对LTE‐Advanced蜂窝部署环境下的ISI建模问题。其中一种模型在[5]中报道，该模型使用系统级仿真器，针对站点间距离（ISD）分别为500米和1732米的两种特定第三代合作伙伴计划（3GPP）蜂窝部署场景进行了研究。文献[5]以不同信干噪比（SINR）条件下的主导干扰比例（DIP）中值来建模干扰。在[5]的干扰建模方法中，用户设备（UE）按照均匀六边形网格均匀分布在中心基站（BS）周围。实际因素，如部署的非均匀性、建筑物/地形效应、用户设备（UE）的不规则分布以及次级干扰强度（IsecI）的影响，在[5]中未被考虑。

一种计算高效的ISI建模方法在[6]中被提出，以减少仿真时间。然而，该研究未提供任何关于干扰的统计或模型。文献[7]为异构LTE‐Advanced网络开发了解析SINR模型，但忽略了来自同类小区的干扰。文献[8]为均匀LTE‐Advanced部署提出了SINR的解析模型。[7]和[8]均假设了简单的瑞利信道，且未考虑无线阴影效应。文献[9]基于Suzuki衰落模型，针对LTE‐Advanced网络中六边形结构及基站的随机分布，提出了ISI的拉普拉斯变换模型。上述假设不适用于实际系统级研究。此外，这些研究均未考虑或建模次级干扰强度。

许多干扰建模研究适用于特定场景和技术。在[10]进行了一次测量活动，以提取信道脉冲响应（CIR）来自无人机（UAV）到两个郊区不同现网LTE小区的下行链路（DL）信道冲激响应。所获得的实测CIR被用于推导最大似然估计器，以获取各链路的信号功率并建模干扰水平。还在[11]开展了测量活动，以测量无人机辅助的无小区通信所用共享频段中的现有干扰水平。测量结果在[11]中被用于开发一个解析框架，利用随机几何工具对无人机应用中的频谱占用进行建模。在[12]中提出了一种通用框架，用于建模无人机辅助的无小区车联网通信中的信干比（SIR）。[12]中的SIR模型考虑了地面车对车和固定对车场景下的网络干扰。[12]中的SIR模型包含了越级率、平均衰落持续时间、空间自协方差和相干距离的解析表达式。

在[13]中提出了一种理论近似，用于建模全维多输入多输出（MIMO）系统上行链路（UL）中由视距（LoS）用户设备（UE）引起的小区内干扰。假设为三维（3D）城市微小区场景，小区半径为100米，基站天线高度为10米。研究假设用户设备采用单天线系统，基站配备平面天线阵列。基站在接收小区扇区内所有用户设备信号时执行三维波束成形（BF）。在[13]中，作者指出LoS干扰用户设备链路的干扰信号与3D BF天线方向图相关，并且是干扰用户设备链路间距的函数。在[14]中提出了一种针对毫米波信号的跨层干扰模型，该模型利用随机几何方法考虑了定向天线和环境遮挡。IEEE 802.15兴趣组在[15]中为低功耗广域网（LPWANs）开发了一种系统间干扰模型，以研究来自其他系统的干扰信号的影响。在[16]中基于随机几何提出了非正交多址接入系统上行信道干扰信号的拉普拉斯变换，在[17]中提出了下行信道的相应变换。

许多研究考虑了在同一频段内同时运行的多种无线技术所产生的共存干扰[18]–[22]，以及同频全双工（IBFD）无线通信系统中的自干扰（SI）[23]–[25]。在[18]中，作者提出了两种不同的方法，基于齐次泊松点过程网络中的干扰分布以及对α‐μ分布的精确近似，来建模聚合干扰信号。基于在医院进行的网络实验，为[19]中的聚合干扰开发了时频和基于簇的统计模型。研究[19]调查并建模了标准化Wi‐Fi和蓝牙设备对在2.4 GHz工业、科学和医疗频段内运行的非标准化医疗设备所产生的聚合干扰影响。

文献[20]和[21]提出了干扰建模方法，用于计算第五代移动通信系统（5G）（IMT‐2020）对现有卫星服务造成的干扰。针对超宽带中聚合干扰信号的分布函数基于实际测量，文献[22]中提出了一种频谱模型。结果显示，测得的聚合干扰信号遵循高斯混合分布，其Kullback‐Leibler散度小于0.05。

在[23]中提出了一种用于全双工无线通信系统中自干扰的模型，该模型支持为上行链路和下行链路选择不同的时频偏移、不同数量的子载波以及不同的符号长度。文献[24]针对微小区和宏小区环境，分别建立了基于几何的同心椭圆和基于几何的同心圆统计信道模型，以对全双工系统中的自干扰信号与期望信号进行建模。文献[25]基于在全双工MIMO系统中测得的自干扰数据，开发了一种二维特定位置的几何随机信道模型。文献[25]的模型包含了光滑墙壁和移动散射体，并提供了MIMO自干扰信道的时延、角度和极化特性。

确定性射线追踪信道模型（RTCM）和标准化的基于几何的随机信道模型（GSCM）是蜂窝系统中用于干扰研究的两种常见信道建模方法。GSCM包括ITU‐R模型[26]、3GPP三维空间信道模型SCM[27]以及METIS 5G模型[28]。这些信道模型根据预定义的系统布局和配置，为各个基站‐用户设备链路提供信道冲激响应（CIR）和信道特性。图1显示了一个蜂窝系统的示例，每个基站包含三个扇区，且频率复用因子为1。图中展示了一个服务基站及其周围的六个第一层干扰基站站点。实心绿线表示服务基站‐用户设备链路，虚线表示干扰基站‐用户设备链路。符号间干扰源由红色虚线表示，而蓝色虚线表示二次干扰源。

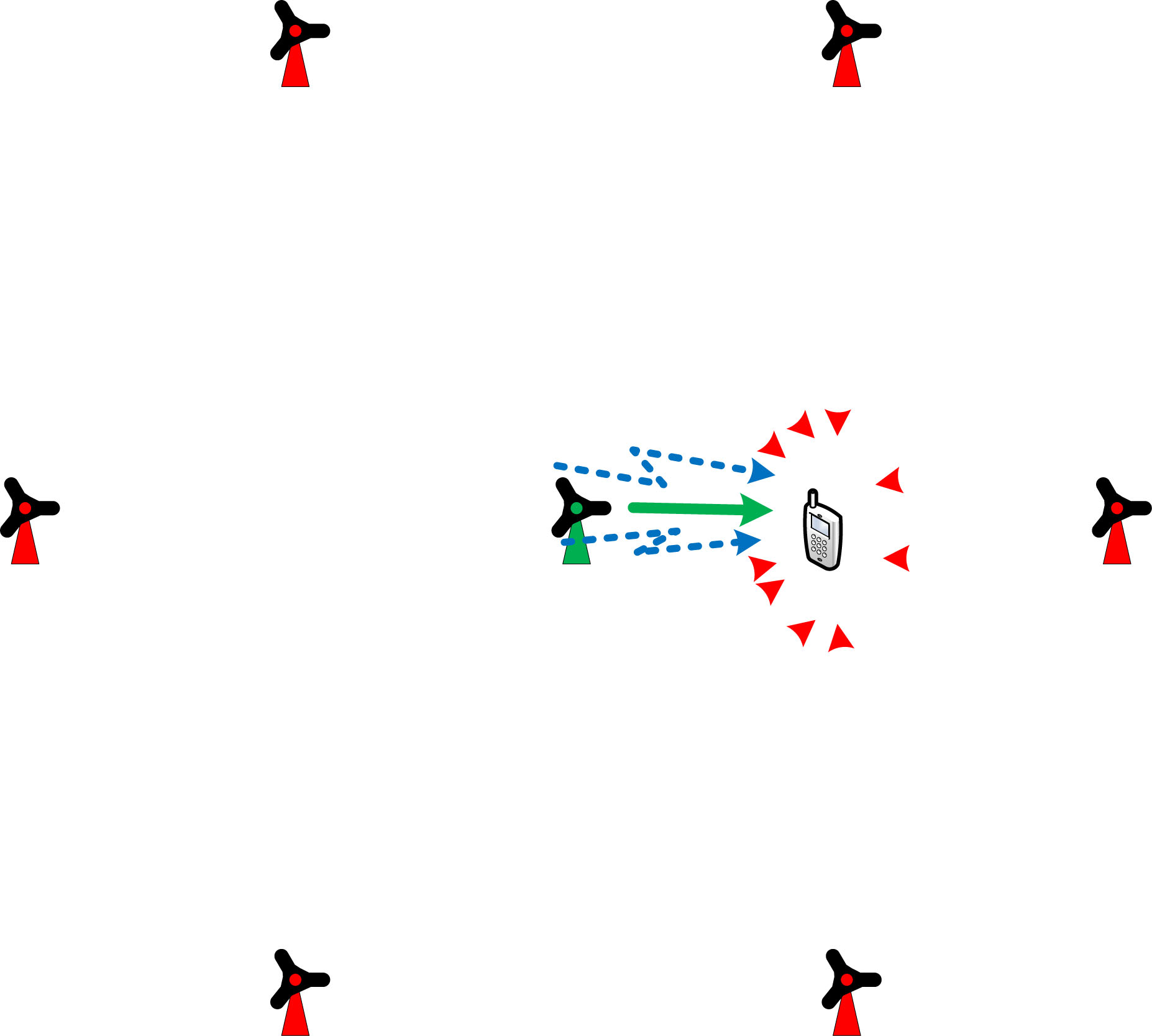
此外，根据相对位置和方向，符号间干扰可能来自一个扇区（一条红色虚线）或两个扇区（两条红色虚线）。为了计算用户设备位置处的信干噪比，在图1中使用RTCM或标准化的GSCM时，必须对12个独立链路应用信道生成过程，以计算所需的信道参数。现有的标准化信道模型均无法直接计算ICI信号。该过程耗时较长，尤其对于涉及大量小区和用户设备（UE）的系统级研究而言。

如前所述，现有文献中的可用干扰模型要么不适用于真实的长期演进‐高级系统场景，要么仅针对特定场景和其他无线技术进行。此外，该领域的先前研究均针对特定的小区尺寸和载波频率开展。而且，这些研究均未提供与国际电信联盟‐无线电通信部门信道模型[26]兼容的符号间干扰和次级干扰强度的独立模型。同时，现有的标准化信道模型也均未提供从服务基站站点的系统布局直接计算符号间干扰和次级干扰强度的方法。

本文的目标是研究、验证和建模频率复用因子为1的长期演进‐高级网络中ICI对不同小区范围、环境和频段的影响。具体目标如下。

1) 研究在遵循3GPP三扇区六边形网格的长期演进‐高级同构网络中，小区范围为（500米、750米、1000米、1250米）、假设基站天线高度为30米[5]的realistic宏小区场景下的ICI影响。采用基于地图的三维RTCM来表征服务和干扰基站‐用户设备链路的传播特性。该研究在两个城市环境中的800 MHz和2.6 GHz载波频率下进行：英国布里斯托尔市中心16平方公里区域和英国伦敦市中心140平方公里区域。选择800 MHz和2.6 GHz频段是为了与长期演进‐高级Release 11[29]的频分双工模式下EUTRA频段7和20之间的带间载波聚合（称为CA_7‐20）保持一致。

2) 验证我们从站点间伦敦的干扰基站射线追踪预测与3GPP测量结果的对比在累积分布函数（CDF）方面以及DIP[30]的中值。

3) 提出基于用户设备（UE）相对于服务基站位置的符号间干扰（ISI）和次级干扰强度（IsecI）的新颖独立模型，该模型遵循标准化的ITU‐R GSCM方法。这一新提出的扩展完全兼容——并可添加到——标准化的ITU‐R模型中。这些独立模型能够更准确地估计干扰水平，并有助于增强干扰消除和抑制技术的设计与性能分析。

4) 提供不同环境和小区范围下的干扰与信道建模参数，以路径损耗指数值表示。这使得所提出的模型可用于研究具有不同传播条件的多种环境。

本文的其余部分组织如下：第二节介绍了包括信道模型和网络布局在内的系统模型。在第三节中，在将符号间干扰和次级干扰强度建模为用户设备相对于服务基站位置的函数之前，对其进行了验证。最后，第四节得出了相关结论。

II. 系统模型

A. 三维射线追踪信道模型

本研究使用布里斯托大学的室外三维射线追踪器来表征服务链路和干扰基站‐用户设备链路的传播特性。该模型为每个基站到用户设备的链路提供三维多径分量的点对点预测。信道被建模为一组包含幅度、相位、时延、到达与出发的仰角以及到达与出发的方位角信息的空间和时间多径分量（MPCs）。该模型识别出基站与用户设备之间的所有直射、透射、单次散射、两次散射以及多次绕射的射线路径。物理路径追踪使用特定站点的不规则地形、三维建筑和植被结构数据库进行。该模型最初由塔梅和尼克斯于1995年开发，并在过去25年中持续改进。该模型的输出已通过与400 MHz至2.6 GHz载波频率范围内的实测数据直接对比得到验证。图2显示了一个示例基站‐用户设备链路的预测多径分量。链路两端采用全向天线建模，具体的天线图通过后处理的空间和极化卷积过程加以应用。这种确定性的RTCM方法相较于标准的国际电信联盟无线电通信组几何随机信道模型具有以下优势：

• GSCM假设了简化的角度扩展分布[26]。
• GSCM的随机过程基于在宽频率范围内定义的分布函数和统计特性。例如，国际电信联盟‐无线电通信部门（ITU‐R）信道模型中报告的城市宏小区场景下视距（LoS）用户设备位置的均方根（RMS）时延扩展（DS）去相关距离，在450 MHz至6 GHz频率范围内为30米。然而，我们先前在[32]中的工作基于在800 MHz和2.6 GHz载波频率下的三维射线建模表明，去相关距离与频率相关。
• 我们的射线追踪器提供的三维统计特性可建立更为准确的模型，因为此前的研究已表明，假设方位角受限的二维传播会导致系统级性能评估不准确[33]。
• 该三维射线模型基于地图，可用于研究多种特定站点的部署场景。

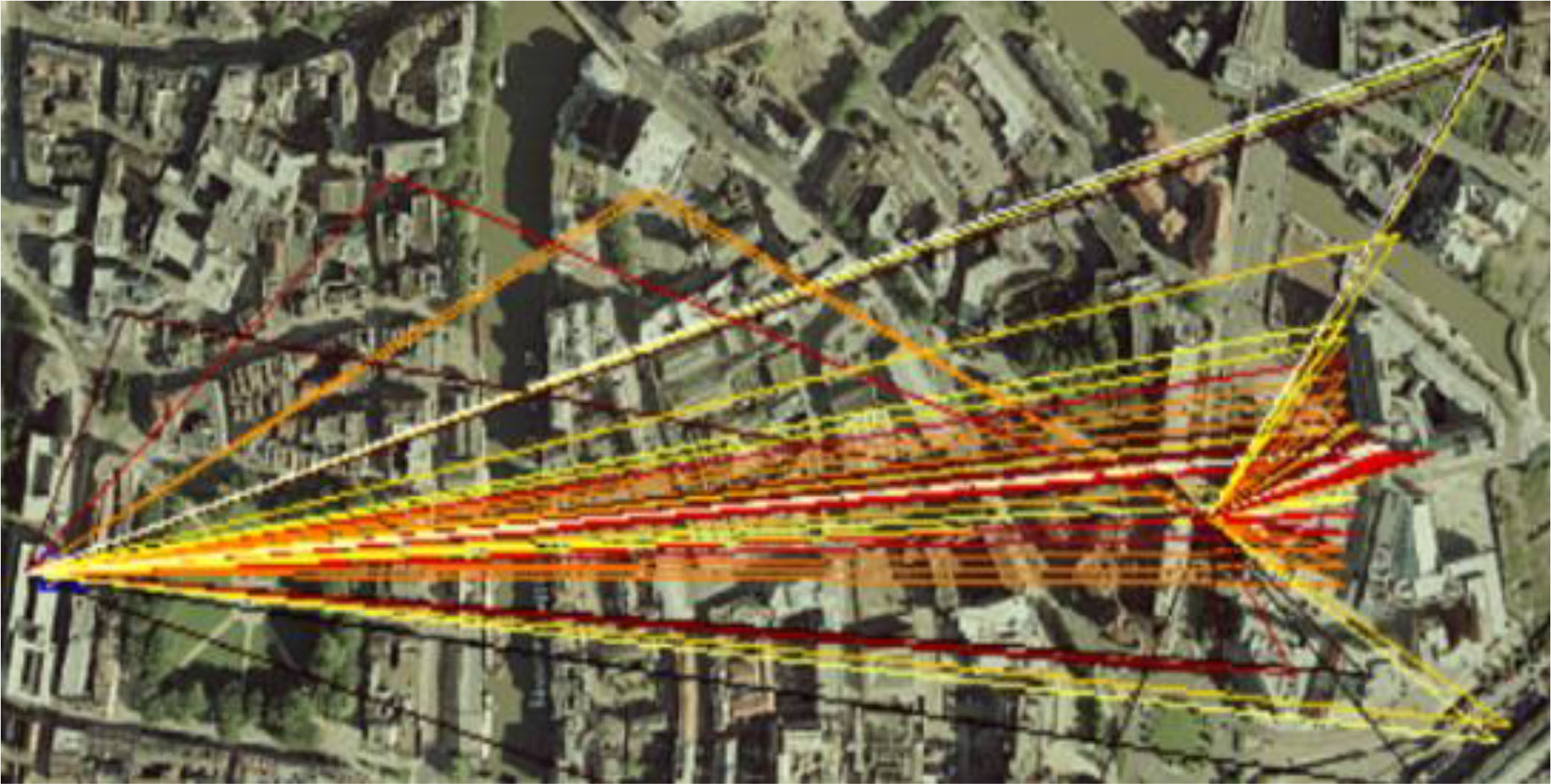
B. 网络布局

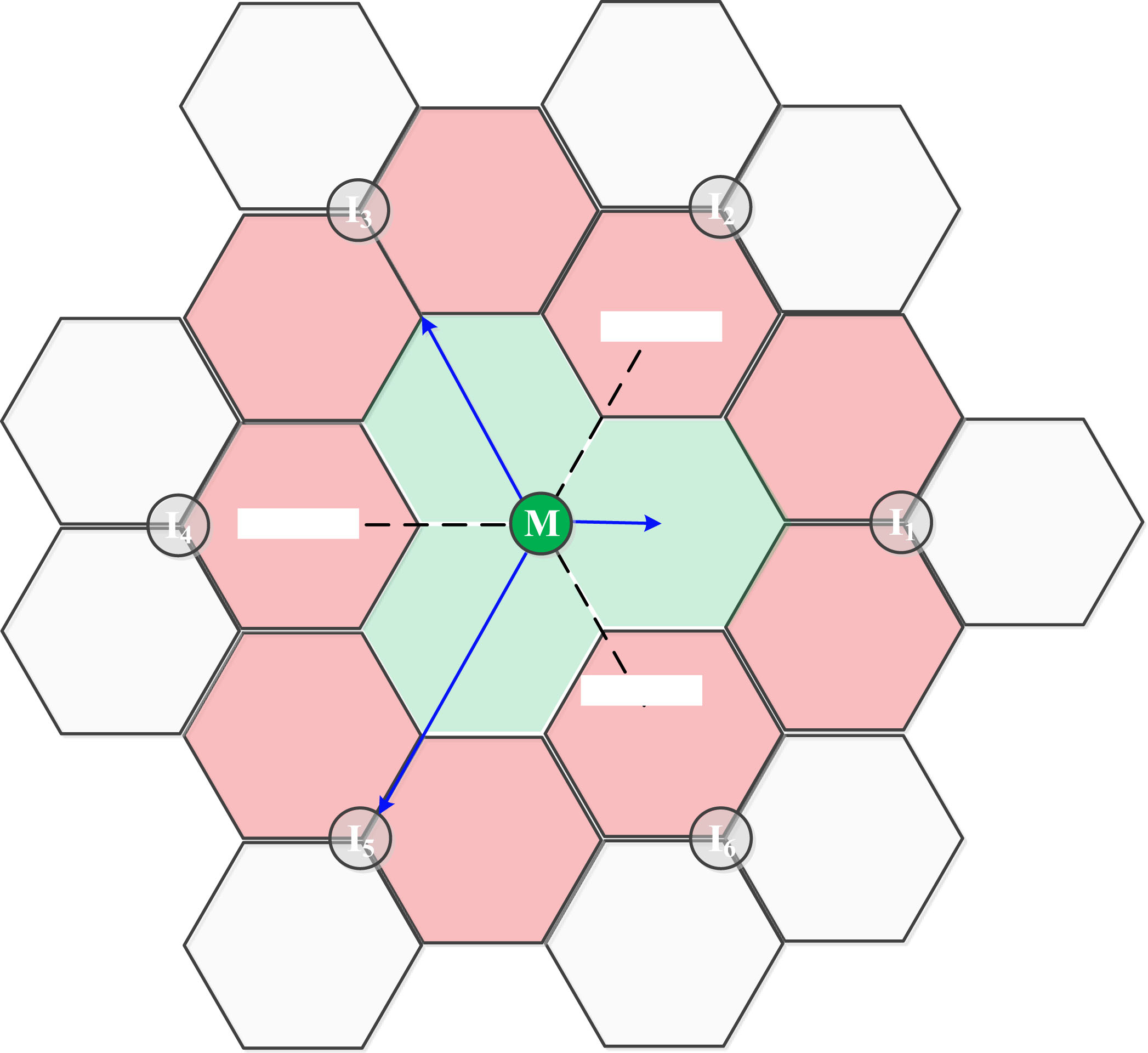
长期演进‐高级系统基于第三代合作伙伴计划宏蜂窝部署，采用频率复用因子为1。如图3所示，每个基站站点由三个扇区组成，小区半径为R，部署在站点间距离为3R、小区范围为2R[2]的六边形网格上。在每个小区内，与文献[5]中报道的系统级仿真器不同，不同的用户设备（UE）被随机分布在街道层面。本研究针对两种不同城市环境中的不同小区范围和载波频率进行。第一个区域是英国布里斯托尔市中心一个4 km × 4.4 km的区域，第二个区域是英国伦敦市中心一个11 km × 13 km的区域。不同小区范围对应的基站发射功率取自[34]。本研究采用了图4所示的宏基站和用户设备天线图。这些天线图由布里斯托大学进行的消声室测量获得[35]。

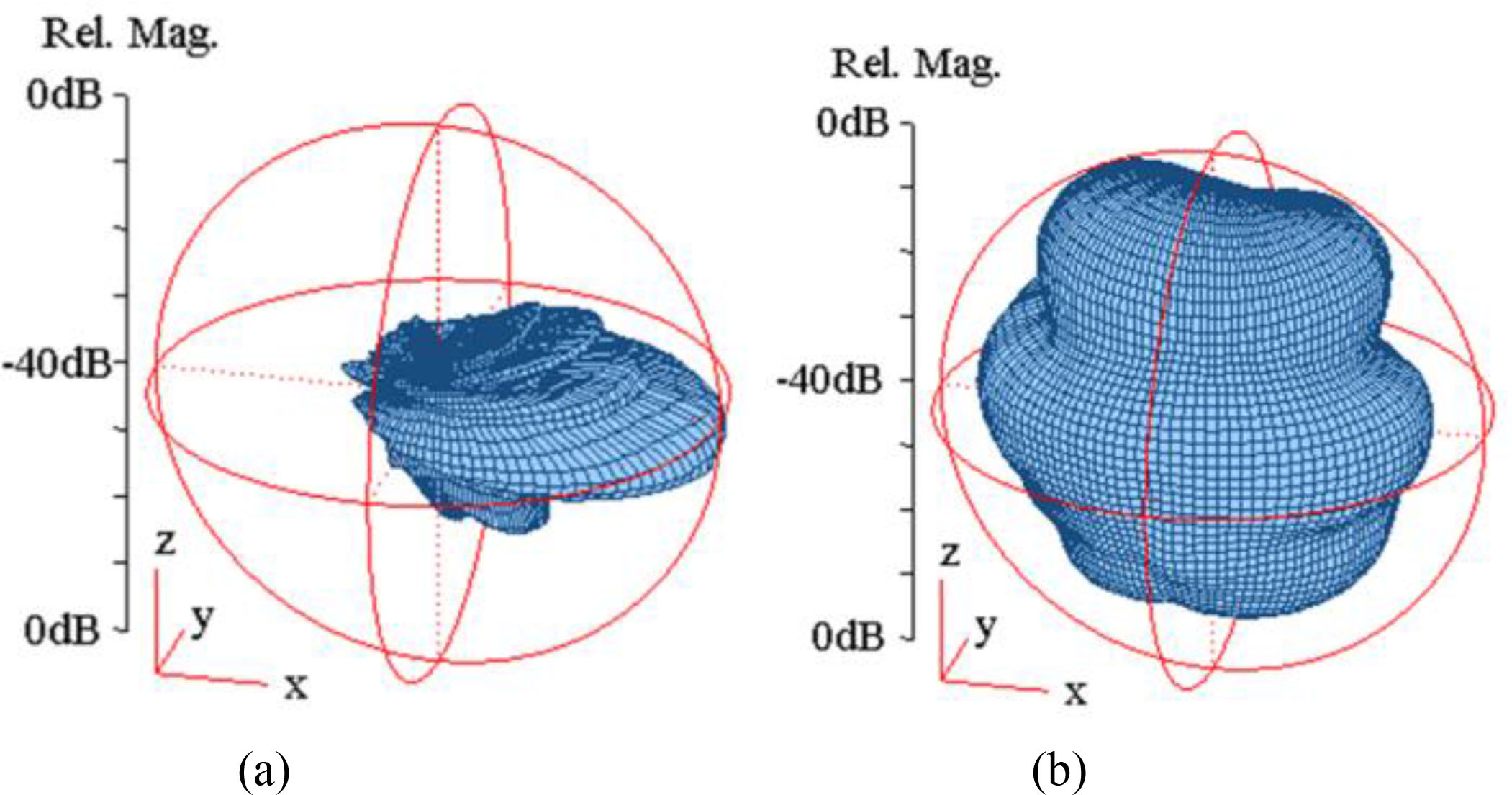
所有天线图均为三维获取，包含相位、极化和方向性信息。

表I 信道模型参数

参数	值
载波频率	800 MHz, 2.6 GHz
小区范围	500 m, 750 m, 1000 m, 1250 m
基站天线高度	30 m
用户设备天线高度	1.5 m
天线增益	见图4

表II 不同用户设备位置的同信道干扰源

用户设备位置	干扰源
主基站-扇区1覆盖区域内	Msector2, Msector3 (IsecI); I1-sector2, I1-sector3, I2-sector3, I3-sector1, I3-sector3, I4-sector1, I5-sector1, I5-sector2, I6-sector2 (ISI)
主基站-扇区2覆盖区域内	Msector1, Msector3 (IsecI); I1-sector1, I1-sector3, I2-sector1, I2-sector2, I3-sector2, I4-sector2, I4-sector3, I5-sector3, I6-sector3 (ISI)
主基站-扇区3覆盖区域内	Msector1, Msector2 (IsecI); I1-sector1, I1-sector2, I2-sector1, I2-sector2, I3-sector1, I3-sector2, I4-sector1, I4-sector2, I5-sector1, I5-sector2, I6-sector1, I6-sector2 (ISI)

在图3中，服务（主）基站站点位于中心，ICI由ISI和IsecI引起。ISI来自围绕服务基站站点的站点间基站的不同扇区，而IsecI表示来自服务基站站点内另外两个扇区的站点内干扰。该方法总结于表II中。例如，考虑位于主基站‐扇区1（Msector1）覆盖区域内的用户设备，主基站站点的另外两个扇区（Msector2、Msector3）是该用户设备的站点内干扰源，定义为IsecI。围绕主基站站点的六个干扰基站站点（I1, I2, I3, I4, I5, I6）引起站点间干扰。共有九个站点间干扰扇区：（I1-sector2、I1-sector3、I2-sector3、I3-sector1、I3-sector3、I4-sector1、I5-sector1、I5-sector2、I6-sector2）。这九个站点间干扰扇区的总干扰功率构成了用户设备处的ISI。

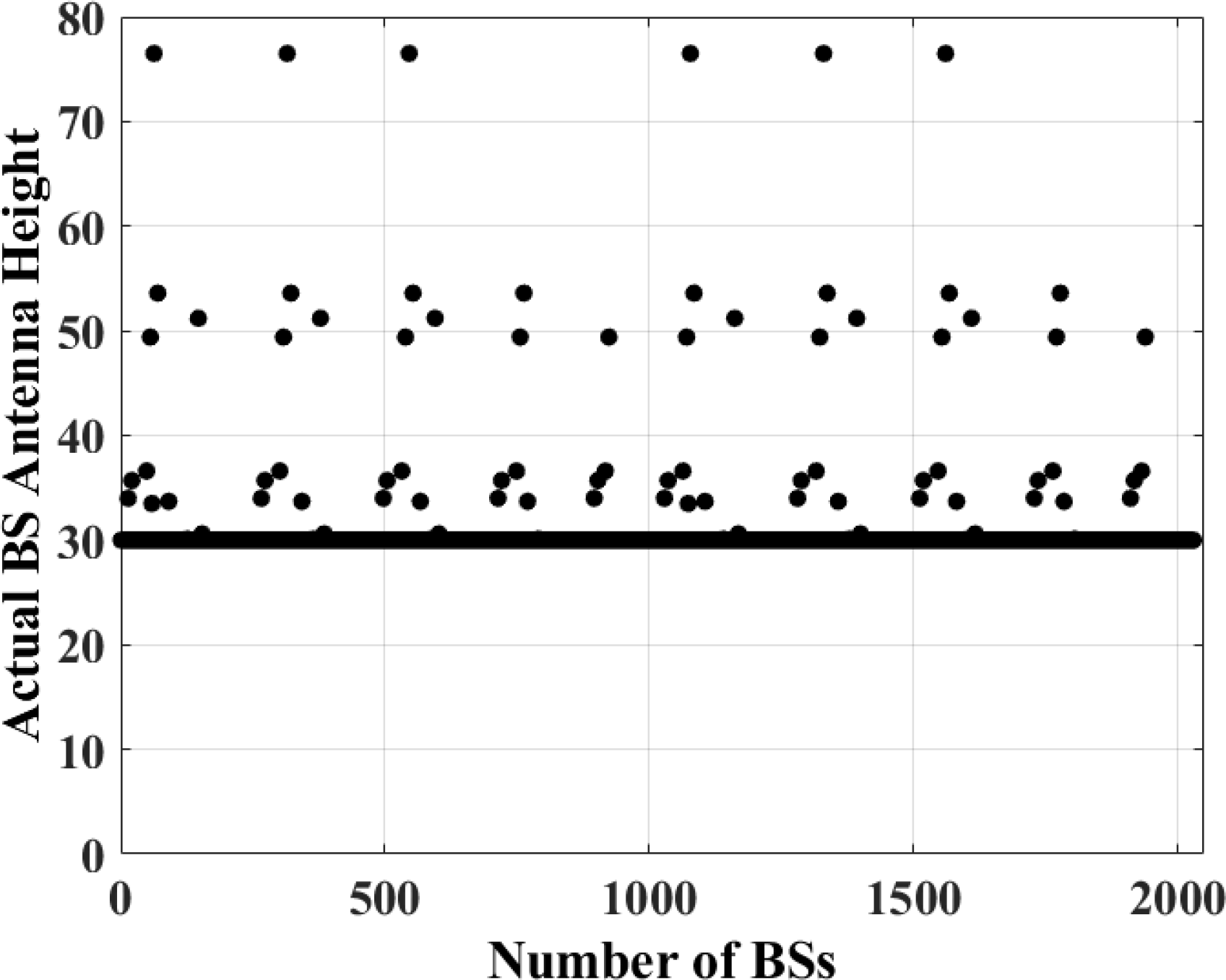
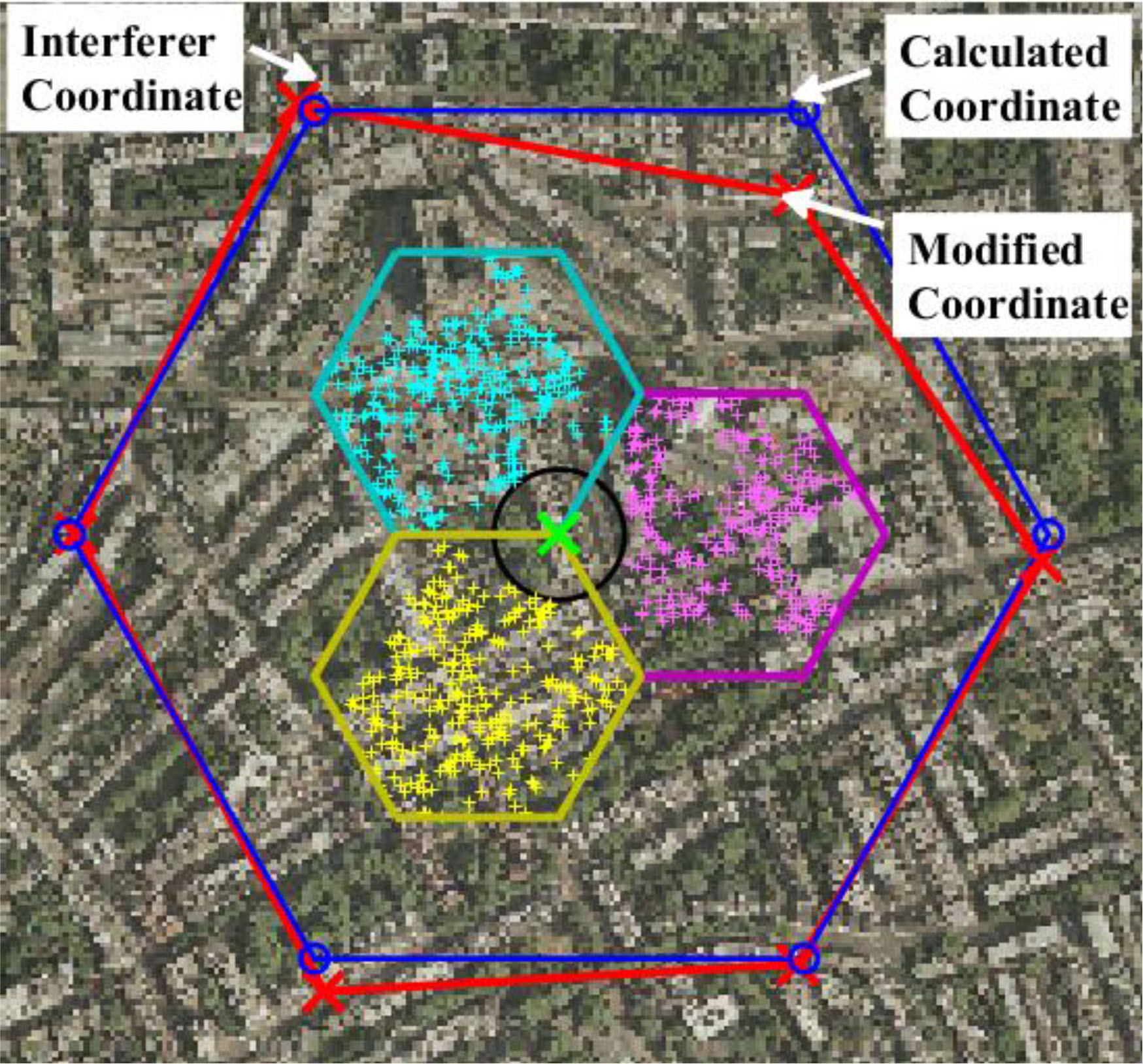
主基站和干扰基站的位置在地图上被选定，以确保基站高度相似。图5显示了本研究中使用的所有基站站点和环境中主基站与干扰基站天线的实际高度。从图5可以明显看出，大多数基站站点的天线高度为30米。然而，部分基站站点的天线高度超过30米。这是由于采用了基于地图的RTCM来部署蜂窝系统，并预测主基站‐用户设备链路和干扰基站‐用户设备链路的多径分量。此外，如图6所示，在RTCM数据库中使用有限的基站位置集合，需要对干扰基站的计算坐标进行调整，从而形成不规则六边形网格。

III. ICI建模

本节通过将符号间干扰（ISI）与次级干扰强度（IsecI）分离来对ICI进行建模。如前所述，ISI来自围绕主基站站点的站点间干扰基站的不同扇区，而IsecI则来自服务基站站点的另外两个扇区，如表II所示。在第三节-A中，我们首先基于累积分布函数（CDF）和中值差分干扰功率（median DIP）[5]，对用户设备（UE）从各个站点间干扰基站接收到的ISI功率进行建模。随后，我们使用先前在伦敦报告的ISI测量结果[30]来验证我们的射线追踪结果。接着，在第三节-B中提出ISI的模型，在第三节-C中提出IsecI的模型，这两个模型均以用户设备（UE）相对于服务基站的位置为函数。这些模型针对两种城市环境、两个载波频率以及四种小区范围进行开发。总ISI功率被建模为与距离相关的模型，而总IsecI功率被建模为主基站处用户设备距离和方位角的函数。

A. DIP建模和符号间干扰验证

本节基于文献[5]所述方法，针对六个第一层干扰站点的DIP，对各个干扰源的符号间干扰功率进行建模和分析。DIP通过公式(1)[5]计算得出：

$$
\text{DIP} {u,j} = \frac{P {u,\text{ISI},j}}{P_{\text{AWGN}} + \sum_{\text{ISI}} P_{u,\text{ISI}}}
\tag{1}
$$

在(1)中，$\text{DIP} {u,j}$表示在用户设备位置 $u$处，来自第$j$-强干扰基站的接收功率与加性高斯白噪声（AWGN）功率 $P {\text{AWGN}}$ 以及总符号间干扰功率 $P_{u,\text{ISI}}$ 之和的比值。

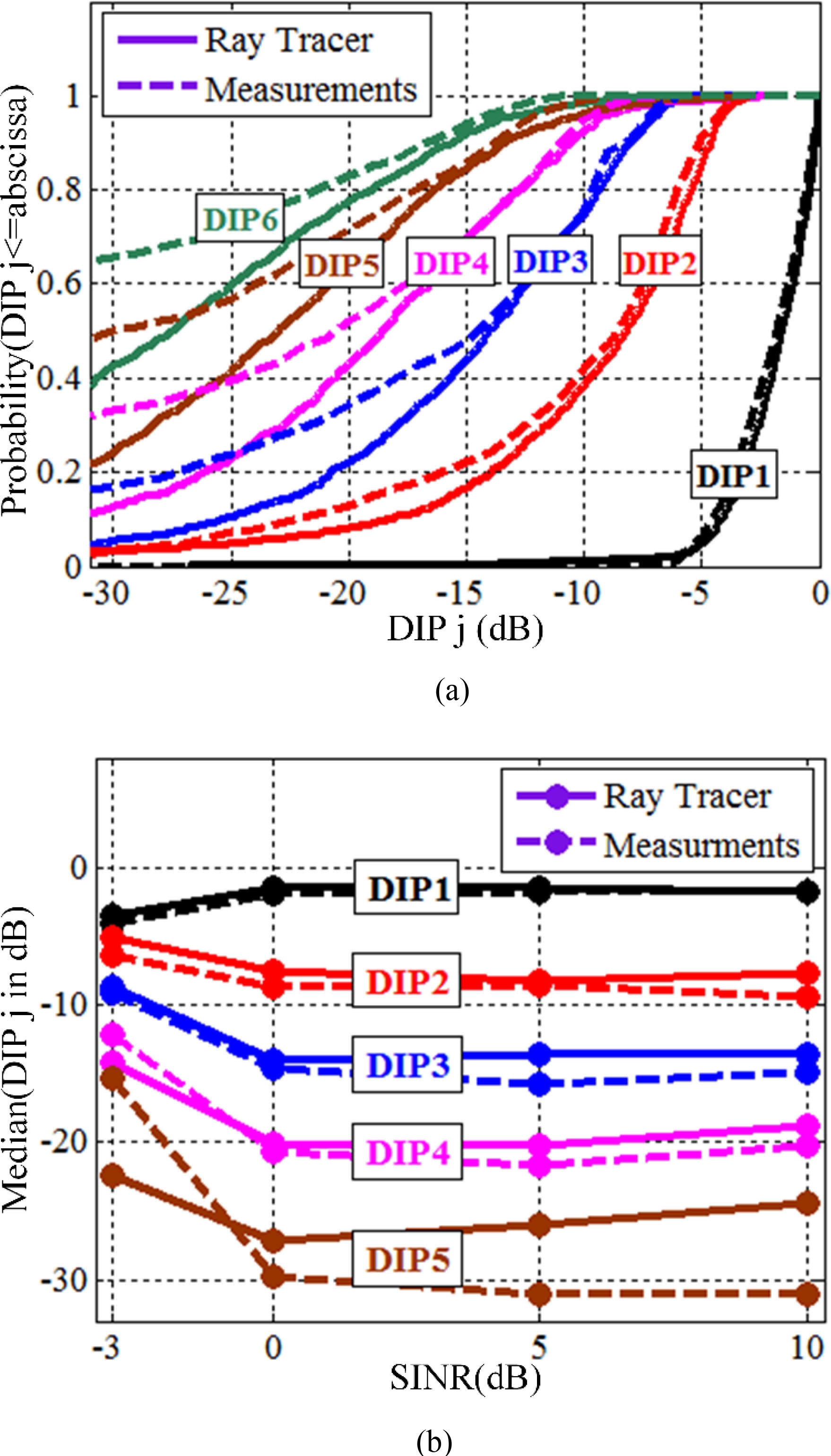
射线追踪工具：载波频率. GHz，站点间距离 m；测量：载波频率 GHz，站点间距离 m。（a）信干噪比为0分贝时 DIP的累积分布函数。（b）不同信干噪比值下的DIP中值。

图7显示了在伦敦，小区范围为750米（ISD= 1125 m）、基站天线高度为30米、载波频率为2.6 GHz时的DIP的累积分布函数和中值。我们的预测与[30]中的测量结果进行了比较。这些测量也是在伦敦进行的，载波频率为2吉赫兹，站点间距离为1000米。图7(a)显示了围绕服务基站的六个干扰基站站点在信干噪比为0分贝时的DIP累积分布函数。将我们的射线模型得到的DIP累积分布函数曲线与[30]的测量结果进行比较，可以看出DIP1和DIP2, 吻合良好，其他DIP值在特定范围内也较为接近。此外，从图7(b)可以明显看出，射线追踪模型在不同信干噪比下的中值差分干扰功率曲线与伦敦测量结果[30]非常接近，但DIP5值除外。注意：[30]中的测量结果报告的中值差分干扰功率值仅到DIP5为止。

B. 符号间干扰的距离相关建模

在本节中，我们考虑用户设备（UE）接收到的总符号间干扰功率，并推导出该功率作为UE与服务基站之间距离函数的模型。图(a)和图(b)分别显示了在布里斯托尔、载波频率为800 MHz、小区范围为750米时，UE接收到的总 ISI功率（单位：dBm）的均值和标准差随距离变化的散点图以及最佳拟合曲线，其中距离为$d_{\text{UE}}$。从图8(a)可以明显看出，符号间干扰功率的均值（单位：dBm）随着服务基站‐用户设备距离的增加而增大。这是由于UE与强 ISI干扰源之间的路径损耗效应所致。当UE远离服务基站时，它会更接近强ISI干扰源，导致UE与强ISI干扰源之间的路径损耗减小，从而引起ISI功率均值的增加。然而，如图8(b)所示，ISI功率的标准差的变化趋势与其均值不同，其标准差可近似为一个常数。ISI功率的标准差的影响类似于阴影衰落，具有距离无关性，并且在特定环境中是固定的[26]。

接收到的总ISI功率的概率密度函数（PDF）如图8(c)所示。如图所示，接收到的总ISI功率的直方图具有最优拟合正态PDF。通过应用柯尔莫哥洛夫‐斯米尔诺夫检验（K‐S检验）验证了所推导的最优拟合正态PDF，其提供的K‐S距离为0.019。该较小的K‐S距离值表明，所推导的正态PDF是对测量数据[36]的良好近似。正态分布由特定的均值（μ）和标准差（σ）表征。需要注意的是，均值和标准差的值是从以dBm为单位的干扰功率的对数值计算得出的。使用对数值是为了与ITU‐R模型[26]保持兼容。对于位于距离服务基站$d_{\text{UE}}$处的用户设备，其接收到的总ISI功率（$P_{\text{ISI}}$）在dBm下的均值（$\mu_{\text{ISI}}$）可通过(2)式计算。

$$
\mu_{\text{ISI}} = p_1 \cdot \frac{d_{\text{UE}}}{1000} + p_2
\tag{2}
$$

公式(2)中的参数$p_1$ 和$p_2$ 是根据平均接收ISI功率值的最佳拟合线计算得出的。表III列出了在800 MHz和2.6 GHz载波频率下，布里斯托尔和伦敦不同小区范围对应的$p_1$, $p_2$ 和$\sigma_{\text{ISI}}$。表III还给出了两种环境在不同小区范围下的路径损耗指数$n$。

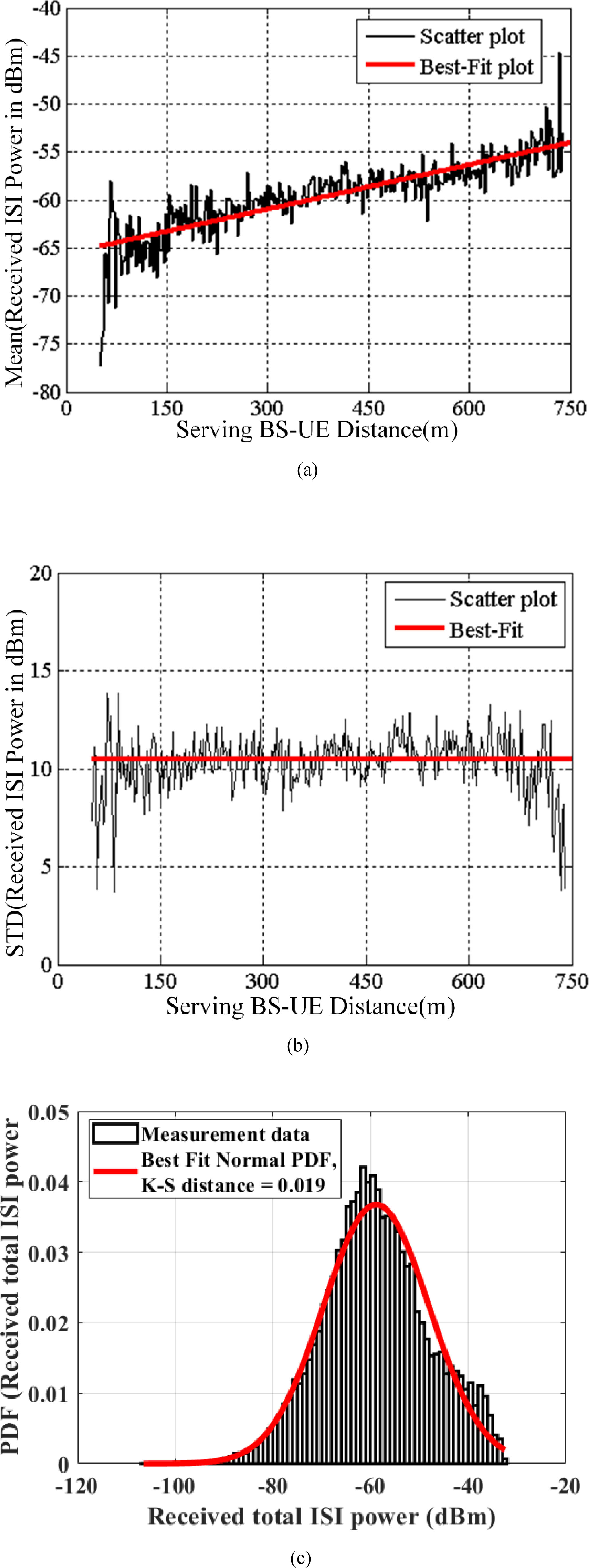接收到的符号间干扰功率的均值。(b) 接收到的符号间干扰功率的标准差。(c) 概率密度函数)

表III 站点间干扰建模参数

环境	载波频率 (MHz)	小区范围 (m)	$p_1$	$p_2$	$\sigma_{\text{ISI}}$ (dB)	路径损耗指数 $n$
布里斯托尔	800	500	1.8	-95.2	6.3	3.1
布里斯托尔	800	750	2.1	-96.5	6.5	3.3
布里斯托尔	800	1000	2.4	-97.8	6.7	3.5
布里斯托尔	800	1250	2.6	-98.9	6.9	3.7
布里斯托尔	2.6	500	2.0	-94.8	6.1	3.0
布里斯托尔	2.6	750	2.3	-96.0	6.4	3.2
布里斯托尔	2.6	1000	2.5	-97.2	6.6	3.4
布里斯托尔	2.6	1250	2.7	-98.3	6.8	3.6
伦敦	800	500	1.6	-95.5	5.9	2.9
伦敦	800	750	1.9	-96.8	6.2	3.1
伦敦	800	1000	2.2	-98.0	6.4	3.3
伦敦	800	1250	2.4	-99.1	6.6	3.5
伦敦	2.6	500	1.7	-95.0	6.0	2.8
伦敦	2.6	750	2.0	-96.3	6.3	3.0
伦敦	2.6	1000	2.3	-97.5	6.5	3.2
伦敦	2.6	1250	2.5	-98.6	6.7	3.4

该表显示，与伦敦相比，布里斯托尔环境的路径损耗指数更高。此外，随着小区范围的增加，路径损耗指数也随之增加。这是因为在更远的距离上遭受了更强的阴影效应所致。

C. 扇区间干扰（IsecI）的建模

在本节中，我们将用户设备（UE）接收到的总IsecI功率建模为UE间距以及相对于服务基站的方位角的函数。

图9显示了在距离服务基站扇区$d_{\text{UE}}$和方位角 $\phi^{\text{sec}}_{\text{UE}}$处，用户设备接收到的总次级干扰强度功率的均值和标准差（单位为分贝毫瓦）。该图针对布里斯托尔地区、小区范围为750米、载波频率为800 MHz的情况绘制。

从图9(a)可以明显看出总IsecI功率的远距离依赖性，其中IsecI功率的均值随着服务基站与用户设备之间的距离$d_{\text{UE}}$的增加而减小。这与ISI均值随服务基站‐用户设备距离变化的趋势不同。因此，将ISI与IsecI区分开来，对于实现准确的性能评估和干扰抑制分析模型至关重要。随着服务基站‐用户设备距离的增加，IsecI源之间的间距也随之增大，导致路径损耗增加，从而降低了IsecI功率的均值。有趣的是，随着服务基站‐用户设备距离的增加，IsecI功率的标准差略有上升。除了距离依赖性外，总 IsecI功率还取决于在扇区内方位平面上服务基站与用户设备之间的夹角($\phi^{\text{sec}}_{\text{UE}}$)。图9(b)显示，当用户设备向扇区边缘移动时，IsecI功率的均值也随之增加，但仍然假设采用恒定的标准差。

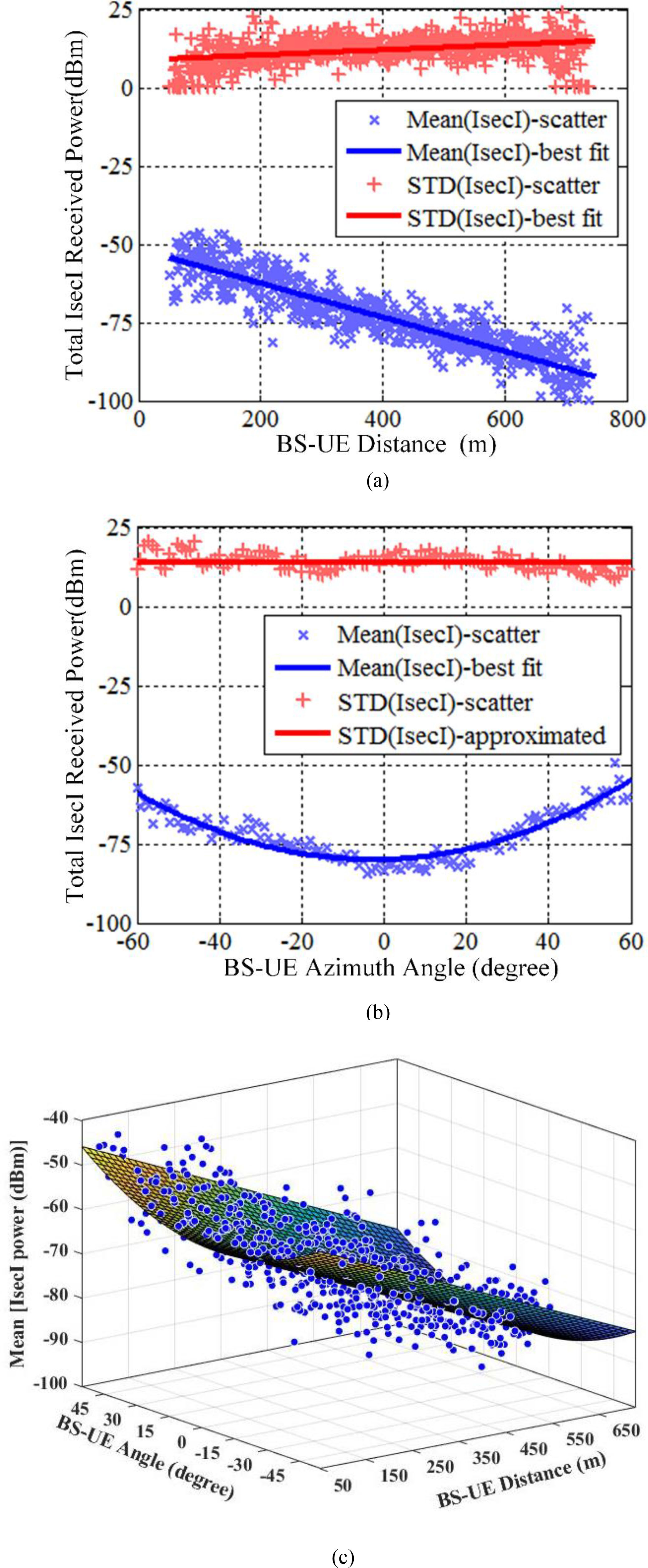次级干扰强度距离依赖性。(b) 次级干扰强度角度依赖性。(c) 总次级干扰强度接收功率均值关于基站与用户设备之间距离和方位角的最佳拟合曲面)

如图9(c)所示，利用MATLAB中的曲线拟合工具，将次级干扰强度功率的均值随距离和角度的变化建模为一个曲面。次级干扰强度功率的均值和标准差是在10米的距离范围和10°的角度范围内计算得出的。均值和标准差随以米为单位的距离的变化基于以下模型进行建模：

一次多项式，而平均IsecI功率的角度依赖性则使用二次多项式进行建模。总IsecI的标准差被假定与方位角无关（见图9(b)），因此仅根据图9(a)将其建模为距离相关的函数。类似于ISI模型，均值和标准差是基于IsecI功率的对数值（单位为分贝毫瓦）计算得出的。用户设备（UE）在距离$d_{\text{UE}}$（单位：米）和角度 $\phi^{\text{sec}} {\text{UE}}$（单位：度）处相对于服务基站的扇区$\delta {\text{UE}}$接收到的总IsecI功率($P_{\text{IsecI}}$)的均值($\mu_{\text{IsecI}}$)（单位：分贝毫瓦）和标准差($\sigma_{\text{IsecI}}$)（单位：分贝）可分别通过公式(3)和(4)计算。角度 $\phi^{\text{sec}} {\text{UE}}$ 在方位面上定义的范围为‐60°至60°，表示扇区 $\delta {\text{UE}}$内UE的角度。角度$\phi^{\text{sec}} {\text{UE}}$ 可通过公式(5)作为方位面上UE角度($\phi {\text{UE}}$)和主站点扇区$\delta_{\text{UE}}$)的函数来计算。(3)和(4)中的参数$p_1$到$p_7$针对布里斯托尔和伦敦不同小区范围的情况分别列于表IV和表V中，对应的载波频率分别为800 MHz和2.6 GHz。

$$
\mu_{\text{IsecI}} = p_1 + p_2 \cdot \frac{d_{\text{UE}}}{10^3} + p_3 \cdot \frac{\phi^{\text{sec}} {\text{UE}}}{10^3} + p_4 \cdot \frac{d {\text{UE}} \cdot \phi^{\text{sec}} {\text{UE}}}{10^6} + p_5 \cdot \frac{(\phi^{\text{sec}} {\text{UE}})^2}{10^3}
\tag{3}
$$

$$
\sigma_{\text{IsecI}} = p_6 \cdot \frac{d_{\text{UE}}}{10^3} + p_7
\tag{4}
$$

$$
\phi^{\text{sec}} {\text{UE}} = \phi {\text{UE}} - 120 \cdot (\delta_{\text{UE}} - 1)
\tag{5}
$$

请注意，图4(a)和图4(b)中所示的宏基站（BS）和用户设备（UE）天线以及基站发射功率的影响已整合到表III、表IV和表V的参数中。此外，附录中的表VI–XVII分别列出了在800 MHz和2.6 GHz载波频率下，伦敦和布里斯托尔不同小区范围的大尺度参数(LSPs)、LSPs的互相关以及LSPs的去相关距离。这些表格可作为对[27]中报告的三维模型的扩展，添加到[26]的国际电信联盟‐无线电通信部门（ITU‐R）通用信道处理方法中。

值得一提的是，在频率复用因子为1的移动网络中，针对特定用户设备位置进行系统级研究时的信干噪比水平计算，需要对12条基站‐用户设备链路进行独立的信道建模（见图1、图3和表II）。其中一条基站‐用户设备链路为主服务基站扇区，其余十一条基站‐用户设备链路由干扰小区产生。两条干扰基站‐用户设备链路用于建模站内扇区的次级干扰强度，其余九条干扰基站‐用户设备链路代表来自周围第一层站间扇区组的符号间干扰。本文提出的同信道干扰方法能够在主基站‐用户设备链路的信道生成过程中实现信干噪比计算，而无需部署其余11个干扰小区，从而显著减少了仿真时间（通常减少约12倍）。

四、结论

本文分析了长期演进‐高级同构网络中的干扰情况。假设系统采用频率复用因子为1进行部署。主基站‐用户设备链路和干扰基站‐用户设备链路之间的通信信道，基于布里斯托尔和伦敦两个真实市中心场景，在两个载波频率下，使用特定站点的基于地图的三维射线追踪工具进行建模。站点间干扰结果首先通过此前在伦敦报告的实地测量数据进行了验证。我们的干扰模型为站点间干扰引入了一种新颖的基站‐用户设备距离相关项，以及用于扇区间干扰建模的基站‐用户设备距离和角度相关项。

我们的距离相关的ISI模型和距离/角度相关的IsecI模型遵循标准化的国际电信联盟无线电通信部门基于几何的随机信道模型。这一新提出的扩展完全兼容，可轻松添加到标准化的国际电信联盟无线电通信部门模型中。由于所提出的模型在生成信道脉冲响应的同时提供了ISI和IsecI，与建模传统第一层干扰小区所需的仿真时间相比，信道生成时间减少了12倍。此外，使用我们的方案无需配置站点间干扰基站的布局，相反，干扰效应可以从服务基站的系统配置中确定。