LeetCode第 189 场周赛（C++）

最新推荐文章于 2024-05-27 21:05:23 发布

原创最新推荐文章于 2024-05-27 21:05:23 发布 · 240 阅读

0 ·

CC 4.0 BY-SA版权

LeetCode 专栏收录该内容

36 篇文章

订阅专栏

本文介绍了四道算法题目，包括计算在特定时间做作业的学生人数、重新排列句子中的单词、寻找独特的收藏清单以及计算圆形靶内的最大飞镖数量。每道题目都提供了详细的解题思路和C++代码实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1、在既定时间做作业的学生人数（3分）

问题描述

给你两个整数数组startTime（开始时间）和 endTime（结束时间），并指定一个整数 queryTime 作为查询时间。

已知，第i名学生在 startTime[i]时开始写作业并于endTime[i]时完成作业。

请返回在查询时间 queryTime时正在做作业的学生人数。形式上，返回能够使 queryTime处于区间[startTime[i], endTime[i]]（含）的学生人数。

示例 1：

输入：startTime = [1,2,3], endTime = [3,2,7], queryTime = 4
输出：1
解释：一共有 3 名学生。
第一名学生在时间 1 开始写作业，并于时间 3 完成作业，在时间 4 没有处于做作业的状态。
第二名学生在时间 2 开始写作业，并于时间 2 完成作业，在时间 4 没有处于做作业的状态。
第二名学生在时间 3 开始写作业，预计于时间 7 完成作业，这是是唯一一名在时间 4 时正在做作业的学生。

示例 2：

输入：startTime = [4], endTime = [4], queryTime = 4
输出：1
解释：在查询时间只有一名学生在做作业。

示例 3：

输入：startTime = [4], endTime = [4], queryTime = 5
输出：0

示例 4：

输入：startTime = [1,1,1,1], endTime = [1,3,2,4], queryTime = 7
输出：0

示例 5：

输入：startTime = [9,8,7,6,5,4,3,2,1], endTime = [10,10,10,10,10,10,10,10,10], queryTime = 5
输出：5

提示：

startTime.length == endTime.length
1 <= startTime.length <= 100
1 <= startTime[i] <= endTime[i] <= 1000
1 <= queryTime <= 1000

解题思路

这道题比较简单，queryTime介于数组中两个对应数字的之间即可，统计符合题意的数组对数。

代码实现

class Solution {
public:
    int busyStudent(vector<int>& startTime, vector<int>& endTime, int queryTime) {
        int count = 0;
        int i = 0, j = 0;
        for(; i < startTime.size(), j < endTime.size(); i++, j++)
        {
            if(startTime[i] <= queryTime and queryTime <= endTime[j])
                count++;
        }
        return count;
    }
};

运行截图

在这里插入图片描述

2、重新排列句子中的单词（4分）

问题描述

句子是一个用空格分隔单词的字符串。给你一个满足下述格式的句子 text:

句子的首字母大写
text中的每个单词都用单个空格分隔。

请你重新排列text中的单词，使所有单词按其长度的升序排列。如果两个单词的长度相同，则保留其在原句子中的相对顺序。
请同样按上述格式返回新的句子。

示例 1：

输入：text = "Leetcode is cool"
输出："Is cool leetcode"
解释：句子中共有 3 个单词，长度为 8 的 "Leetcode" ，长度为 2 的 "is" 以及长度为 4 的 "cool" 。
输出需要按单词的长度升序排列，新句子中的第一个单词首字母需要大写。

示例 2：

输入：text = "Keep calm and code on"
输出："On and keep calm code"
解释：输出的排序情况如下：
"On" 2 个字母。
"and" 3 个字母。
"keep" 4 个字母，因为存在长度相同的其他单词，所以它们之间需要保留在原句子中的相对顺序。
"calm" 4 个字母。
"code" 4 个字母。

示例 3：

输入：text = "To be or not to be"
输出："To be or to be not"

提示：

text 以大写字母开头，然后包含若干小写字母以及单词间的单个空格。
1 <= text.length <= 10^5

解题思路

首字母改成小写text[0] += 32;。
将string text中的单词提取出来，存入到vector<string>中。
将vector<string>中的单词存入到multimap<int, string>中。由于multimap的特点是允许重复出现相同的key并且key值由小到大排列。
依次将multimap<int, string>中的元素存储到新的string textnew中。
首字母大写textnew[0] -= 32;。
补充：我的另一篇博文是有关C++中multimap和map的区别和vecor的使用方法和该题目的另一种解题写法。

代码实现

class Solution {
public:
    string arrangeWords(string text) {
        text[0] += 32; // 转变为小写
        multimap<int, string> ismap;
        int blanknum = count(text.begin(), text.end(), ' ');
        vector<string> svec(blanknum + 1);
        int count = 0, i = 0;
        for (; i < text.size(); i++)
        {
            if (text[i] == ' ')
            {
                count++;
                continue;
            }
            svec[count].push_back(text[i]);
        }
        for (auto& word : svec)
        {
            int size = (int)word.size();
            ismap.insert(pair<int, string>(size, word));
        }
        string textnew;
        for (auto& word : ismap)
        {
            textnew += word.second;
            textnew += " ";
        }
        textnew.pop_back();
        textnew[0] -= 32; // 转变为大写
        return textnew;
    }
};

运行截图

在这里插入图片描述

3、收藏清单（5分）

给你一个数组favoriteCompanies，其中favoriteCompanies[i]是第i名用户收藏的公司清单（下标从0开始）。

请找出不是其他任何人收藏的公司清单的子集的收藏清单，并返回该清单下标。下标需要按升序排列。

示例 1：

输入：favoriteCompanies = [["leetcode","google","facebook"],["google","microsoft"],["google","facebook"],["google"],["amazon"]]
输出：[0,1,4] 
解释：
favoriteCompanies[2]=["google","facebook"] 是 favoriteCompanies[0]=["leetcode","google","facebook"] 的子集。
favoriteCompanies[3]=["google"] 是 favoriteCompanies[0]=["leetcode","google","facebook"] 和 favoriteCompanies[1]=["google","microsoft"] 的子集。
其余的收藏清单均不是其他任何人收藏的公司清单的子集，因此，答案为 [0,1,4] 。

示例 2：

输入：favoriteCompanies = [["leetcode","google","facebook"],["leetcode","amazon"],["facebook","google"]]
输出：[0,1] 
解释：favoriteCompanies[2]=["facebook","google"] 是 favoriteCompanies[0]=["leetcode","google","facebook"] 的子集，因此，答案为 [0,1] 。

示例 3：

输入：favoriteCompanies = [["leetcode"],["google"],["facebook"],["amazon"]]
输出：[0,1,2,3]

提示：

1 <= favoriteCompanies.length <= 100
1 <= favoriteCompanies[i].length <= 500
1 <= favoriteCompanies[i][j].length <= 20
favoriteCompanies[i] 中的所有字符串 各不相同 。
用户收藏的公司清单也 各不相同 ，也就是说，即便我们按字母顺序排序每个清单， favoriteCompanies[i] != favoriteCompanies[j] 仍然成立。
所有字符串仅包含小写英文字母。

解题思路

如果favoriteCompanies只有一个元素，自然返回下标0。
C++中有关集合的函数，需要先对数组中的元素进行排序。
利用嵌套for循环逐个元素检查，但要注意如果嵌套的循环里和外循环中的元素一致时，选择跳过（continue）。
includes(iter2->begin(), iter2->end(), iter1->begin(), iter1->end())含义是如果iter1指向的数组元素含于iter2所指向的数组，返回true否则返回false。
定义整型计时器变量来表示要存储的元素的数组下标。
补充:集合的其他函数是：set_union()：集合的并集；set_intersection()：集合的交集；set_different()：集合的差集。用法：set_different(vec1.begin(), vec1.end(), vec2.begin(), vec2.end(), back_inserter(vec3));：将vec1中vec2不存在的元素，赋值给vec3，如果多次执行，vec3中的元素不会被更新，只会堆叠存放。

代码实现

class Solution {
public:
    vector<int> peopleIndexes(vector<vector<string>>& favoriteCompanies) {
        if(favoriteCompanies.size() == 1)
            return {0};
        int size = favoriteCompanies.size();
        for (auto& str : favoriteCompanies)
            sort(str.begin(), str.end()); // 排序
        vector<vector<string>>::iterator iter1 = favoriteCompanies.begin(), iter2;
        int count = -1, countemp = 0;
        vector<int> list;
        for (; iter1 != favoriteCompanies.end(); iter1++)
        {
            count++;
            for (iter2 = favoriteCompanies.begin(); iter2 != favoriteCompanies.end(); iter2++)
            {
                if (*iter1 == *iter2)
                    continue; // 两个数组元素相等则跳过
                if (includes(iter2->begin(), iter2->end(), iter1->begin(), iter1->end()))
                    break; // 第二个集合中的元素全部来自于第一个集合中的元素 返回true
                countemp++;
            }
            if (countemp == size - 1)//这说明在这轮循环中不存在包含关系 
                list.push_back(count);// count值压入动态数组
            countemp = 0;
        }
        return list;
    }  
};

运行截图

在这里插入图片描述

4、圆形靶内的最大飞镖数量（7分）

问题描述

墙壁上挂着一个圆形的飞镖靶。现在请你蒙着眼睛向靶上投掷飞镖。

投掷到墙上的飞镖用二维平面上的点坐标数组表示。飞镖靶的半径为r。

请返回能够落在任意半径为r的圆形靶内或靶上的最大飞镖数。

示例 1：
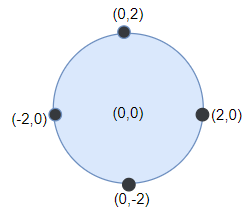
在这里插入图片描述

输入：points = [[-2,0],[2,0],[0,2],[0,-2]], r = 2
输出：4
解释：如果圆形的飞镖靶的圆心为 (0,0) ，半径为 2 ，所有的飞镖都落在靶上，此时落在靶上的飞镖数最大，值为 4 。

示例 2：
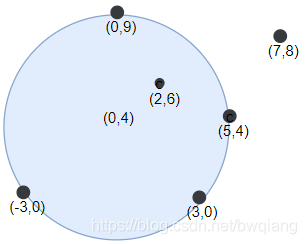
在这里插入图片描述

输入：points = [[-3,0],[3,0],[2,6],[5,4],[0,9],[7,8]], r = 5
输出：5
解释：如果圆形的飞镖靶的圆心为 (0,4) ，半径为 5 ，则除了 (7,8) 之外的飞镖都落在靶上，此时落在靶上的飞镖数最大，值为 5 。

示例 3：

输入：points = [[-2,0],[2,0],[0,2],[0,-2]], r = 1
输出：1

示例 4：

输入：points = [[1,2],[3,5],[1,-1],[2,3],[4,1],[1,3]], r = 2
输出：4

提示：

1 <= points.length <= 100
points[i].length == 2
-10^4 <= points[i][0], points[i][1] <= 10^4
1 <= r <= 5000

解题思路

本题核心思想就是求出在一个给定半径不给定圆心（任意位置）的圆中所能涵盖的最多点的数量。

代码实现

struct point{
    double x,y;
    point(double i,double j):x(i),y(j){}
};

//算两点距离
double dist(double x1,double y1,double x2,double y2){
    return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
}

//计算圆心
point f(point& a,point& b,int r){
    //算中点
    point mid((a.x+b.x)/2.0,(a.y+b.y)/2.0);
    //AB距离的一半
    double d=dist(a.x,a.y,mid.x,mid.y);
    //计算h
    double h=sqrt(r*r-d*d);
    //计算垂线
    point ba(b.x-a.x,b.y-a.y);
    point hd(-ba.y,ba.x);
    double len=sqrt(hd.x*hd.x+hd.y*hd.y);
    hd.x/=len,hd.y/=len;
    hd.x*=h,hd.y*=h;
    return point(hd.x+mid.x,hd.y+mid.y);
}

class Solution {
public:
    int numPoints(vector<vector<int>>& points, int r) {
        int n=points.size();
        int ans=0;
        for(int i=0;i<n;i++){
            for(int j=0;j<n;j++){
                if(i==j){//一个点
                    int cnt=0;
                    for(int k=0;k<n;k++){
                        double tmp=dist(points[i][0],points[i][1],points[k][0],points[k][1]);
                        if(tmp<=r) cnt++;
                    }
                    ans=max(cnt,ans);
                }else{//两个点
                    //通过长度判断有没有圆心
                    double d=dist(points[i][0],points[i][1],points[j][0],points[j][1]);
                    if(d/2>r) continue;

                    point a(points[i][0],points[i][1]),b(points[j][0],points[j][1]);
                    point res=f(a,b,r);
                    int cnt=0;
                    for(int k=0;k<n;k++){
                        double tmp=dist(res.x,res.y,points[k][0],points[k][1]);
                        if(tmp<=r) cnt++;
                    }
                    ans=max(cnt,ans);
                }
            }
        }
        return ans;
    }
};