NYOJ 120 校园网络（强连通分量缩点）

最新推荐文章于 2018-11-05 20:48:20 发布

原创最新推荐文章于 2018-11-05 20:48:20 发布 · 561 阅读

0 ·

CC 4.0 BY-SA版权

图专栏收录该内容

11 篇文章

订阅专栏

本文深入解析了信息技术领域的核心技术和应用，包括但不限于前端开发、后端开发、移动开发、游戏开发、大数据开发等细分领域。通过详细阐述每个领域的关键技术、实践案例以及最新发展趋势，旨在为读者提供全面的技术视野和行业洞察。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

校园网络

时间限制： 3000 ms | 内存限制： 65535 KB

难度： 5

描述

南阳理工学院共有M个系，分别编号1~M,其中各个系之间达成有一定的协议，如果某系有新软件可用时，该系将允许一些其它的系复制并使用该软件。但该允许关系是单向的，即：A系允许B系使用A的软件时，B未必一定允许A使用B的软件。

现在，请你写一个程序，根据各个系之间达成的协议情况，计算出最少需要添加多少个两系之间的这种允许关系，才能使任何一个系有软件使用的时候，其它所有系也都有软件可用。

输入

第一行输入一个整数T，表示测试数据的组数(T<10)
每组测试数据的第一行是一个整数M，表示共有M个系(2<=M<=100)。
随后的M行，每行都有一些整数，其中的第i行表示系i允许这几个系复制并使用系i的软件。每行结尾都是一个0，表示本行输入结束。如果某个系不允许其它任何系使用该系软件，则本行只有一个0.

输出

对于每组测试数据，输出最少需要添加的这种允许关系的个数。

样例输入

样例输出

来源

POJ改编

tarjan算法介绍（求有向图的强连通分量的）

在有向图G中，如果两个顶点可以相互通达，则称两个顶点 强连通(strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个 强连通图。非强连通图有向图的极大强连通子图，称为 强连通分量(strongly connected components)。

下图中，子图{1,2,3,4}为一个强连通分量，因为顶点1,2,3,4两两可达。{5},{6}也分别是两个强连通分量。

Tarjan算法是用来求有向图的强连通分量的。求有向图的强连通分量的Tarjan算法是以其发明者Robert Tarjan命名的。Robert Tarjan还发明了求双连通分量的Tarjan算法。

Tarjan算法是基于对图深度优先搜索的算法，每个强连通分量为搜索树中的一棵子树。搜索时，把当前搜索树中未处理的节点加入一个堆栈，回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。

定义 DFN(u)为节点u搜索的次序编号( 时间戳)，Low(u)为u或u的子树能够追溯到的最早的栈中节点的次序号。

当 DFN(u)=Low(u)时，以u为根的搜索子树上所有节点是一个强连通分量。

接下来是对算法流程的演示。

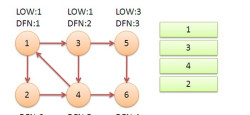
从节点1开始DFS，把遍历到的节点加入栈中。搜索到节点u=6时，DFN[6]=LOW[6]，找到了一个强连通分量。退栈到u=v为止，{6}为一个强连通分量。

返回节点5，发现DFN[5]=LOW[5]，退栈后{5}为一个强连通分量。

返回节点3，继续搜索到节点4，把4加入堆栈。发现节点4向节点1有后向边，节点1还在栈中，所以LOW[4]=1。节点6已经出栈，(4,6)是横叉边，返回3，(3,4)为树枝边，所以LOW[3]=LOW[4]=1。

继续回到节点1，最后访问节点2。访问边(2,4)，4还在栈中，所以LOW[2]=DFN[4]=5。返回1后，发现DFN[1]=LOW[1]，把栈中节点全部取出，组成一个连通分量{1,3,4,2}。

至此，算法结束。经过该算法，求出了图中全部的三个强连通分量{1,3,4,2},{5},{6}。

可以发现，运行Tarjan算法的过程中，每个顶点都被访问了一次，且只进出了一次堆栈，每条边也只被访问了一次，所以该算法的时间复杂度为O(N+M)。

其实这道题说的是强连通缩点就是把只有各个连通图的根节点留下，其他去掉，让几个根节点连通来求解

// 强连通分量缩点

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<stack>
#include<cstring>
using namespace std;
int map[105][105];
int DNF[105],low[105],IN[105],OUT[105],t[105],instack[105];
int min(int a,int b){return a > b ? b : a;}
int V,res,order;
stack<int> S;

int tarjan(int u)
{
int v;
DNF[u] = low[u] = ++order;
instack[u]=1;
S.push(u);
for(int i = 1; i <= V; i++){
if(map[u][i]){
if(!DNF[i]){
tarjan(i);
low[u]=min(low[u],low[i]);
}
else if(instack[i])low[u]=min(low[u],DNF[i]);
}
}
if(DNF[u]==low[u]){
++res; // res 代表强连通分量的个数
do{
v = S.top();
S.pop();
instack[v]=0;
t[v]=res;
}while(v != u);
}
}

int main()
{
int test;
scanf("%d",&test);
while(test--){
int x;
memset(map, 0, sizeof(map)); //用矩阵存放数据
memset(DNF, 0, sizeof(DNF)); // 节点搜索的次序编号
memset(low, 0, sizeof(low)); //记录强连通分量的根节点
memset(IN, 0, sizeof(IN)); //统计入度
memset(OUT, 0, sizeof(OUT)); //统计出度
memset(t, 0, sizeof(t));
memset(instack, 0, sizeof(instack)); //判断节点是否在栈中
while(!S.empty())
S.pop();
res=0;
order=0;
scanf("%d",&V);
for(int i = 1; i <= V; i++){
while(~scanf("%d",&x)&&x)
map[i][x] = 1;
}
for(int i = 1;i <= V;i++){
if(!DNF[i])tarjan(i);
}
//使原有的图经过强连通分量缩点变成只有res个强连通分量的节点的图
for(int i = 1; i <= V; i++){
for(int j = 1; j <= V; j++){
if(map[i][j]){ // 统计每个强连通分量缩点的入度和出度
++IN[t[i]];
++OUT[t[j]];
}
}
}
int m=0,n=0;
for(int i = 1; i <= res; i++){
if(IN[i]==0)m++;
else if(OUT[i]==0)n++;
}
int count = m > n? m : n; // 结果为缩点后的有向图中出度为0或者入度为0中的大者

if(res==1)printf("0\n");
else printf("%d\n",count);
}
return 0;
}