光照归一化人脸识别综述

基于光照归一化分类法的人脸识别

1 引言

实时应用中的关键挑战是不同光照条件下的人脸识别。尽管已有多种光照滤波技术，但这些方法被认为较为陈旧，且对光照滤波技术性能的深入分析尚不充分[1, 2]。当前的人脸识别技术包含一组用于光照归一化的功能，有助于应对人脸识别系统中的这一关键挑战[3]。光度归一化中使用的大多数技术被用于开发本工具箱中的方法[4]，这些技术用于在实际处理阶段之前完成光照归一化。可以看出，这与在分类或建模阶段补偿由光照引起外观变化的方法截然不同[5, 6]。

2 光照归一化人脸识别

光照变化。基本上，这些方法可以分为三大类。 展示了光照滤波的分类法。

• 光照归一化
• 光照建模
• 光照不变性特征提取

2.1 光照归一化

主类别指的是在光照变化下的归一化人脸图像。该类别的典型算法包括小波、可控滤波、基于非局部均值以及自适应非局部均值。

2.1.1 基于小波（WA）

杜和沃德是首个引入基于小波的归一化（WA）技术[7]的人。该技术对图像进行离散的小波变换，然后进行处理。获得的子带。将基于估计的变换’s系数对详细系数ficient的矩阵[8]进行直方图均衡化。当子带被处理后，我们可以通过逆向小波变换重新设计归一化图像[9, 10]。

人们可以观察到，离散小波变换根据八度频带树结构实现信号的多分辨率分解。双带小波变换可使信号通过小波显现出来。此外，基于尺度的功能也可按顺序在不同尺度上进行[11]。

$$
f \left(x\right)= \sum_k a_{o, k}\phi_{o, k}\left(x\right)+ \sum_i\sum_k d_{j, k}\psi_{j, k}\left(x\right) \quad \left(1\right)
$$

其中 $\phi_{j, k}$ 和 $\psi_{wj, k}$ 分别为尺度j上的尺度功能和小波功能。此外，$A_{j, k}$ 和 $D_{j, k}$ 分别为尺度系数和小波系数（ ）。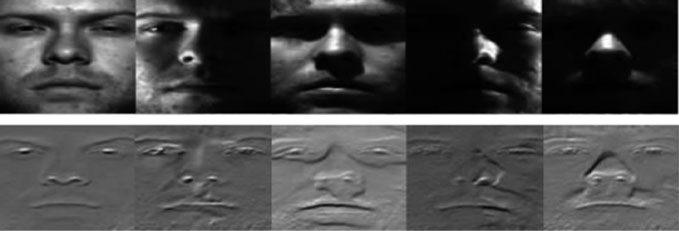

2.1.2 基于可控滤波

为了消除人脸图像中由外观变化引起的光照影响，采用了第二种技术，即基于可控滤波的SF归一化方法。在方向性人脸[12, 13]上可以看到大量不规则小块。因此，通过使用可控金字塔分解[14, 15]，面部图像中的特征可以在不同尺度上被划分为多个包含估计和细节的子带。当子带组合数量较多时，将不可避免地增加合理的约束，因为单级衰减不足以有效分离这些特征。为了更好地捕捉面部图像中的多方向信息，必须直接测量所有方向的导数，但这会带来较高的计算成本。根据可控滤波理论[16, 17],，可通过某些功能进行插值

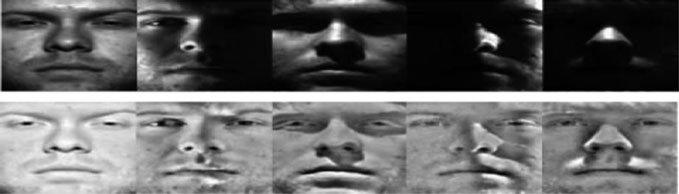
在图像的导数上进行方向性处理，即为基本导数。每个人脸和虹膜图像的数据库可以通过分解为3个层级和6种方向的子带来创建。直接的S‐P系数中的无关和冗余信息使得差异化特征无法被完全去除[18, 19]。

因此，应对每个S‐P子带中一组大小相似的块以有序且不重叠的方式进行划分，以实现对人脸和虹膜图像的局部且有效的表示。可以应用诸如能量、均值、差异以及S‐P系数能量分布在各个子带层次分解后的熵等统计度量，以根据普遍认知识别纹理基础。如果$I_{ij}(x, y)$是第i个子带中第j个特定块的图像，则生成的特征向量为 $\nu_{ij} = (\text{均值}, \text{方差}, \text{能量或熵})$；

$$
\text{Mean}= \frac{1}{M \times N} \sum_{M}^{x= 1} \sum_{N}^{y= 1} I\left(x, y\right) j j \quad \left(2\right)
$$

$$
\text{Variance}= \frac{1}{M \times N} \sum_{M}^{x= 1} \sum_{N}^{y= 1} \left(I_{ij}\left(x, y\right)−\mu_{ij}\right)^2 \quad \left(3\right)
$$

$$
\text{Enrgy}= \sum_{M}^{x= 1} \sum_{N}^{y= 1} \left|I_{ij}\left(x, y\right)\right|^2 \quad \left(4\right)
$$

其中M和N是$I_{ij}(x, y)$的尺寸。熵是一种用于衡量随机性的统计指标，用来表示输入图像的纹理特征。熵的描述如下

$$
\text{Entropy}= -\sum_{p} \left(p \times \log\left(p\right)\right) \quad \left(5\right)
$$

其中p包含直方图的数量。通过将每个块的测量值连接成一个大的特征向量，其中 $\nu=\bigcup_{k}^{i= 1}\bigcup_{k_i}^{j=1}{\nu_{ij}}$。k表示S‐P子带的数量，$K_i$表示第i个子带中的块数，从而构建人脸和虹膜的特征向量。因此，该技术能够在保留主要判别信息的同时提取最佳特征并减小数据规模（ ）。

2.1.3 基于非局部均值的

结构 帕韦希奇 还要求熟悉这些 非局部的 基于 标准化(NLM)[16] 的 策略。在此 技术 中， 亮度 目的将被输入

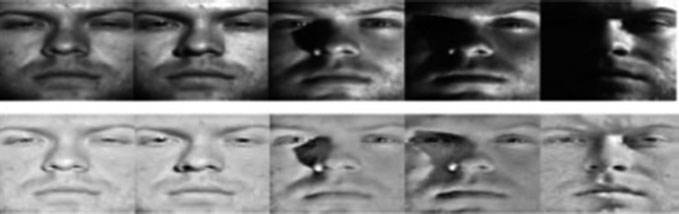
非局部去噪意图的计算，该计算随后用于figure 那些反射率[17, 20]。这些算法对应于非局部方法，简称为 NL 方法[21, 22]将构成一种去噪系统图像，该系统是近期提出的一种不同于显示去噪方法的方法，主要在于从整幅图像像素到噪声抑制目标的处理方式[23]。这归因于若干相似窗口，这些窗口可能在每个小图像的窗口内被识别出来’。此外，这些窗口中的每一个都可能用于图像去噪设计[16, 24]。假设噪声污染后的图像为 $I_n(x) \in R^{a \times b}$，其中 A 和 b 由图像尺寸的像素确定，此外，令’s 设 x 表示噪声图像中任意像素位置 $x=(x, y)$。NL 方法的计算过程将去噪后的图像 $I_d(x)$ 定义为：对 $I_n(x)$ 中像素值取加权平均，作为 $I_d(x)$ 中每个像素值的输入。

$$
I_d\left(x\right)= \sum_{x\in I_n\left(x\right)} \omega\left(z, x\right)I_n\left(x\right) \quad \left(6\right)
$$

$w(z, x)$ 是用于计算像素邻域在空间位置z和x之间相似性的权重函数。此处的权重函数将在下文进行描述。

$$
\omega\left(z, x\right)= \frac{1}{z\left(z\right)} e^{-\frac{G_\partial \left|I_n\left(\Omega_x\right)-I_n\left(\Omega_z\right)\right|}{h^2}} \quad \text{and} \quad Z\left(z\right)= \sum_{x\in I_n\left(x\right)} e^{-\frac{G_\partial \left|I_n\left(\Omega_x\right)-I_n\left(\Omega_z\right)\right|}{h^2}} \quad \left(7\right)
$$

上述公式表明，$G_\sigma$是一个标准差为s的高斯核，$O_x$和$O_z$分别是位置x和 z处像素的局部邻域。h表示控制指数函数衰减的参数，Z(z)是归一化因子 （ ）。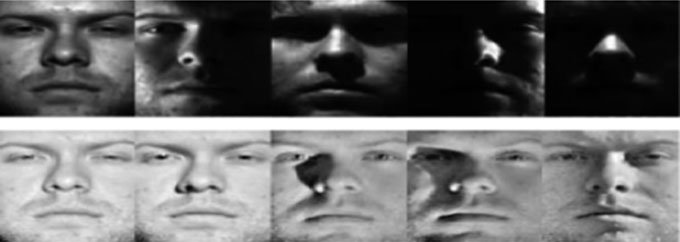

2.1.4 自适应非局部均值

ANL 是一种多功能非局部均值构建的归一化简写形式，可能已被引入到‘ Štruc 什么’此外 Pavešić [16]。在此技术中，用于多功能非局部均值去噪的算法将被用来测量关于亮度追踪的目的，最终 Tom’在计算反射率数值时进行查阅flectance number [25]。该多功能非局部均值通道与小波混合的方式将与 NLM filter 类似。然而，平滑参数通常会被调整，这也可能被表达出来。

$$
\sigma^2= \min\left(d\left(R_i, R_j\right)\right)\forall≠i\quad\text{and}\quad R= \mu−Ψ\left(\mu\right) \quad \left(8\right)
$$

其中体积R是通过减去唯一的含噪体积u和低通filtered volume ψ(μ)测得距离的输入。通过使用最小算子去除低频输入，实验表明，此种情况下需要一个与$s^2$近似相同的最小距离[26, 27]。这种简单方法具有两个显著的fi优点：首先，可以找到具有相似结构但均值水平不同的相同图像块，以补偿现有数据的强度同质性[28, 29]。然而，在搜索数据库中伴随唯一图像块时，会导致对此种情况下的噪声方差产生最小程度的高估。因此，参数$h^2$将通过类似于式（Eq. fi8）中最小距离计算的自适应滤波来确定8( 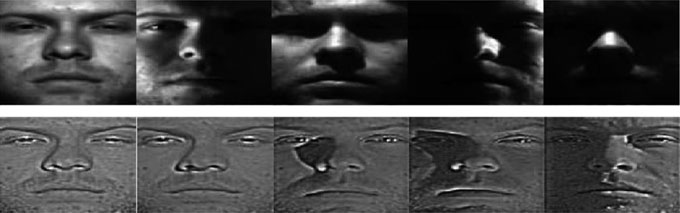的性能——反射功能 [26]))。

2.2 光照建模

在第二类中，不同光照条件下的图像构建需要考虑特定表面反射特性的假设 [6,30]。光照变化可以通过第二类的典型算法（如 SSR、 MSR和 ASR）进行很好的建模[31, 32]。

2.2.1 单尺度视网膜(SSR)

单尺度视网膜算法（SSR）被提出[33, 34]，该算法与光度归一化技术有许多相似之处[35, 36]。当SSR尺度较低时，局部对比度会得到改善，这间接使得鲁棒压缩范围变得更优。然而，光晕伪影将成为此处的主要缺点之一。但是，随着SSR尺度的增加，颜色恒常性特征也会同时得到改善，但这并不能显著压缩图像的鲁棒尺度，因为它未考虑图像特性’。[37, 38]这是由于图像的’压缩鲁棒尺度比率的变化所致[18,39]。SSR形式可以定义为（fined as(9)，

$$
R\left(x, y\right)= \log I\left(x, y\right)− \log\left(F\left(x.y\right)* I\left(x, y\right)\right) \quad \left(9\right)
$$

其中 $R(x, y)$ 是视网膜输出；$I (x, y)$ 是图像强度；‘*’ reflects 表示卷积操作；而 $F(x, y)$ 是高斯函数（ ）。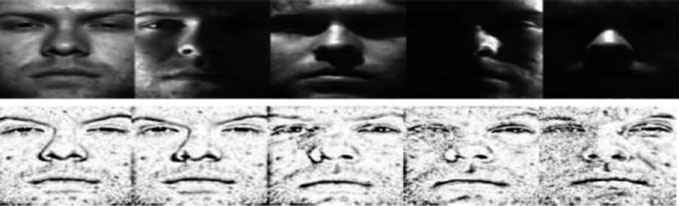

$$
F\left(x, y\right)= K \cdot e^{-\left(x^2+ y^2\right)}, \quad \text{integral}\left(\text{integral}\left(F\left(x, y\right)\right)\right), dx, dy= 1, \quad \left(10\right)
$$

2.2.2 多尺度Retinex（MSR）

多尺度视网膜算法（MSR）是从SSR扩展而来的算法[21]。Retinex理论中的一个假设是，颜色的感知完全依赖于人类视觉系统的神经结构[40, 41]。这进而引入了用于亮度计算的Retinex模型[40, 42]Land’s理论是在首个基于Retinex理论提出的SSR之后应用并建立的，随后发展为MSR[41, 43]。MSR成功地改善了局部对比度以及鲁棒压缩的范围。最近的研究也发现了从多个角度增强MSR的方法，例如颜色校正[44–46]（ ）。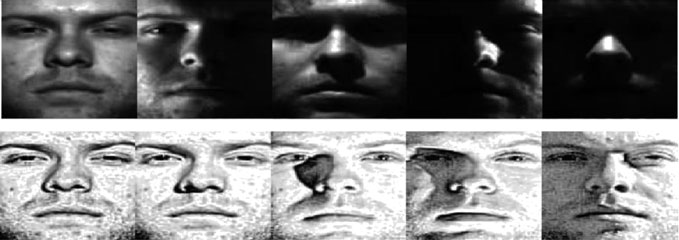

2.2.3 自适应单尺度Retinex（ASR）

正如研究所建议的，自适应单尺度视网膜（ASR）算法需要获取Retinex策略的最新附加组件[47]。来自SSR的不同图像的混合以及与每个SSR尺度相关的权重，应当是基于ASR中从图像信息内容自适应获得的权重的那些点 [48, 49]。最初，将使用红色、蓝色和绿色的转换来恢复亮度Y部分以输入图像颜色。这可以通过应用如下所示的功能方程实现。

$$
Y\left(x, y\right)= 0.299 \cdot R\left(x, y\right)+ 0.587 \cdot G\left(x, y\right)+ 0.114 \cdot B\left(x, y\right) \quad \left(11\right)
$$

其中 $R(x, y)$、$B(x, y)$ 和 $G(x, y)$ 表示位于 $(x, y)$ 处的红色、蓝色和绿色像素的值。随后，所提出的自适应多尺度Retinex（AMSR）技术将处理 Y 亮度图像以得到增强的亮度图像 $Y_{AMSR}$（ ）。

2.3 照明不变特征提取

第三类的目标是寻找在不同光照条件下人脸图像中光照变化的潜在表示。第三类中使用的典型算法包括离散余弦变换、各向同性扩散、MAS 和 DoG。

2.3.1 基于同态滤波的归一化（HOMO）

HOMO是Homomorphicfiltering的缩写，是一种流行的归一化技术，该技术将图像输入转换为相应的对数，然后转换到频域[50, 51]。接着，会增强高频成分，而降低低频成分。最后，通过使用逆傅里叶变换将图像恢复回空间域[52]（ ）。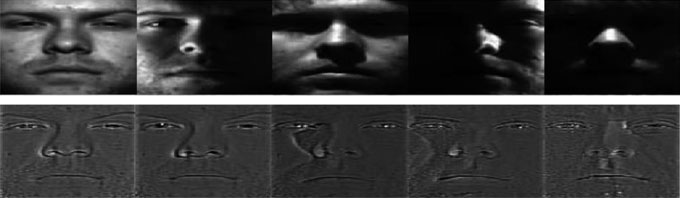

光照部分可能在二维傅里叶变换中被发现，该变换处理图像的对数，因为在二维傅里叶频谱的外部区域对应反射率部分。通常，在傅里叶空间中，亮度和反射率部分无法直接区分[36, 53]。

这些片段可能会被适当地隔离，但无论如何，这取决于同态通道的适宜性参数。通常情况下，这些参数的设定会基于研究人员’的经验达到平衡。例如，根据阿德尔曼’的观点，他将这些同态筛选技术与不同的适宜性参数设置相关联，而这些设置仅仅是冰山一角，还需满足预期要求。在[53, 54]的研究中，关于同态参数质量的静态聚合需根据其在应用同态筛选动机中的计算经验来确定。正如[55]所述，来自同类通道和参数的各种质量被评估，以选择出大部分情况下最适宜的一个。该数据集可能fi用于确定这些参数’的选择技术，适用于任何系统。因此，强烈建议采用全局差异变量（GCF）[49]来构建选择系统，以确定同态参数，从而使其在任意数据库中都具备自主性。[57]

2.3.2 离散余弦变换(DCT)

离散余弦变换在不同的人脸识别研究中被广泛应用于特征提取阶段[58–60]。通过将对应低频的DCT系数设为零，该技术可实现光照不变性ficientsthat corresponds from low frequencies to zero [61–63]。一种彻底的局部外观基于方法，不考虑数据的空间主体，同时在分类过程中使用DCT特征。如今，已有大量研究致力于减少亮度变化的影响，以及姿态变化带来的更大影响’taccount to thespatial majority of thedata employments DCT features same time doing the clas-sification. Nowadays, there are a numberinvestigations bring been directed[64, 65] centering on the way on decrease those sway for brightening variety What’smoreimpact from claimingpose variety 66 。

2.3.3 基于各向同性扩散的归一化

基于各向同性扩散的标准化方法（简称IS）可能在之前利用各向同性平滑对图像进行处理，以分析亮度的目的。

系统重新反射各向异性扩散为基础的标准化系统的重排r变体[67, 68]。各向异性分散（AD）的计算因其在人脸图像上的亮度不变性去除特性而广受欢迎’。然而，用于传导目的的不连续性度量会影响各向异性传播算法的工作 [67]。通常，在各向异性传播的传统计算中，不连续性估计可交替地从非均匀性或空间梯度中选取[54]。人脸图像可根据如下类似方程进行反射处理：

$$
I\left(x, y\right)= R\left(x, y\right) L\left(x, y\right). \quad \left(12\right)
$$

如(12)所述，$R(x, y)$通常指代场景中的所有反射。同时$I(x, y)$表示亮度。因此，通过确定光照$L(x, y)$，面部周围光照的标准化可能得以验证并进一步实现。由于病态问题，无法根据$I(x, y)$直接计算$L(x, y)$。通常假设$R(x, y)$比 $L(x, y)$变化更剧烈。因此，通过识别图像’的$I(x, y)$对数与其平滑形式（即 $L(x, y)$的近似估计）之间的差异，在大多数情况下可以恢复$R(x, y)$。噪声可通过对数处理消除，从而简化估计过程。该方法被称为非特定商图像，其基本框架及非特定商图像策略将在后续图示中进一步说明（见图’ ）。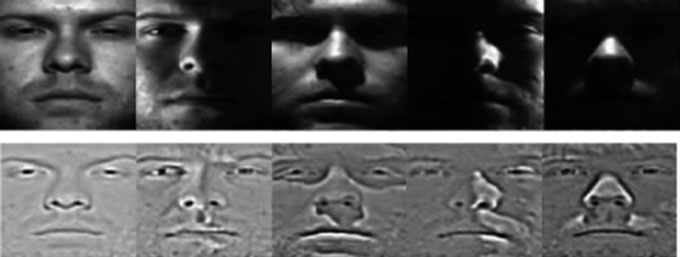

2.3.4 修正的各向异性扩散(MAD)

用于归一化的修正的各向异性扩散方法被称为修正的各向异性扩散归一化 （MAS），该方法由格罗斯和布拉约维奇提出[67, 69]。该方法在原始技术基础上进行了两项改进：（a）引入了更具动态性的估计局部对比度，增加了新的功能。通过这一新功能，现在能够在对比度计算中对由于原始面部图像中像素强度接近0而产生的极端值进行饱和处理；（b）在最后阶段应用了一种动态的后处理过程（由谭和特里格提出，年份）。

正如佩罗纳和马利克所述，他们建议各向异性传播的数学表述为各向异性传播方法中的特定图像平滑提供了一个系统[70]。已有确切的创新性研究工作通过分数阶微分的数学表述应用于各向异性传播，从而在图像中保护基本结构。除了各向异性传播方法外，多尺度技术[71–74]也被引入以进一步降低超声图像[74–76]中的斑点。

通常，各向异性传播可被视为一种非线性图像多尺度变换策略，用于在边缘保持和噪声去除之间实现理想的平衡。第一幅图像的尺度可通过应用高斯部分的高斯表示进行卷积处理。在图像分析结构的多尺度系统中进行扩散比较时应用了这一特定思想[77]。根据佩罗纳和马利克[70]的研究，可能已经设计出一种多尺度平滑和边缘检测方法，最终通过在图像基于扩散的滤波策略中利用图像梯度来实现。这可以生成能够帮助保留图像边缘的自适应滤波器。

$$
I_{t+\Delta t}^{i.j} = I_t^{i.j} + \frac{\Delta t}{|\eta_{i.j}|} \sum_{p \in \eta_{i.j}} c\nabla I_t^{i.j} p.\left(\left(\nabla I_t^{i.j}\right)_p\right) \quad \left(13\right)
$$

在公式（13）中，$I_t^{ij}$ 将是那些像素位置$(i, j)$处离散采样的图像，$\eta_{i,j}$ 是像素$(i, j)$的空间邻域， $|\eta_{i, j}|$ 是邻域窗口内像素的度量，$\Delta t$ 是长时间步长跨度。自适应滤波系统的变异系数此前已被应用，在 Yu 和 Acton’的[78]研究中被用来替代梯度驱动的扩散系数 $c((\nabla I_t^{ij})_p)$，并被称为即时变异系数，或简称 ICOV（ ）。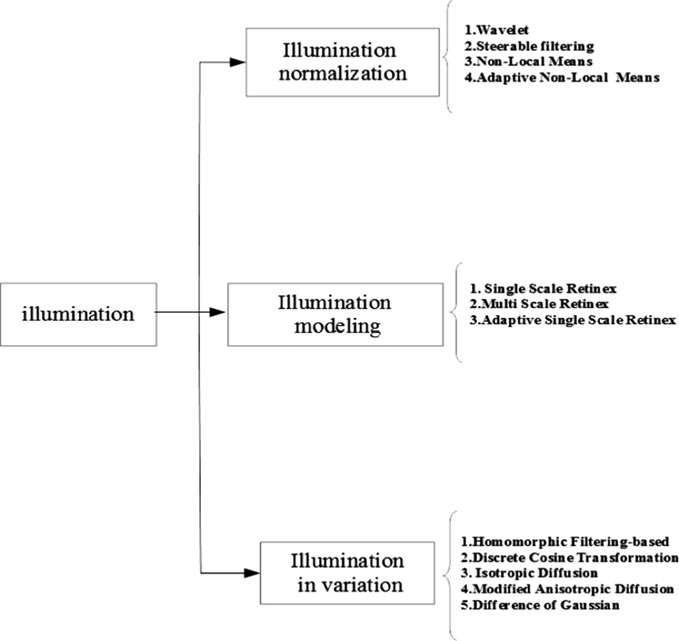

2.3.5 高斯差分（DoG）

依赖高斯滤波器变化来生成归一化图像的光照归一化方法称为基于高斯差分滤波的归一化，或简称为高斯差分[2, 10, 32]。基本上，该方法利用对输入图像进行带通筛选，从而产生归一化版本。在应用滤波器之前，必须先对图像进行伽马校正或对数变换，否则将难以获得期望的结果[30]。人们还可以借鉴汤姆’的文献中的频域策略，采用光照‐反射率模型，通过灰度层次化来增强图像表现，并在同一过程中对增强效果进行区分和整合[51, 79]。在此模型中，每个像素值$f(x, y)$可被视为由照度分量$i(x, y)$和反射分量$r(x, y)$相乘得到的结果，如下面的公式（14）所示反射分量$r(x, y)$相乘得到的结果，如下面的comparison(14)所示

$$
f \left(x, y\right)= i\left(x, y\right)r\left(x, y\right) \quad \left(14\right)
$$

在公式（14）附近进行对数转换的部分将分离这两个自由部分。此外，这种划分方法可能随后有机会在公式（15）下被转换。

$$
z\left(x, y\right)= \ln f\left(x, y\right)= \ln i\left(x, y\right)+ \ln r\left(x, y\right) \quad \left(15\right)
$$

如果 $z(x, y)$ 经过滤波函数 $h$ 处理，结果是“*”，表示两个函数的卷积。这可以根据卷积理论推导为：

$$
s\left(x, y\right)= h z\left(x, y\right)= h \ln i\left(x, y\right)+ \ln r\left(x, y\right) \quad \left(16\right)
$$

$$
s\left(\mu, v\right)= H\left(\mu, v\right)Z\left(\mu, v\right)= H\left(\mu, v\right)F_i\left(\mu, v\right)+ H\left(\mu, v\right)F_r\left(\mu, v\right) \quad \left(17\right)
$$

其中 $S(u, v)$、$H(u, v)$、$Z(u, v)$、$F_i(u, v)$ 和 $F_r(u, v)$ 分别是 $s(x, y)$、$h(x, y)$、 $z(x, y)$、$\ln i(x, y)$ 和 $\ln r(x, y)$ 的单独傅里叶变换。之后，通过逆傅里叶变换计算 $s(x, y)$，如公式(18)所示：

$$
s\left(x, y\right)= \mathfrak{I}^{-1}{s\left(\mu, v\right)} \quad \left(18\right) = \mathfrak{I}^{-1}{H\left(\mu, v\right)}F_i\left(\mu, v\right)}+ \mathfrak{I}^{-1}{H\left(\mu, v\right)}F_r\left(\mu, v\right)}
$$

其中 $\mathfrak{I}^{-1}$ 是逆傅里叶变换算子。

set

$$
i\left(x, y\right)= \mathfrak{I}^{-1}{H\left(\mu, v\right)}F_i\left(\mu, v\right)} \quad \left(19\right)
$$

and

$$
r\left(x, y\right)= \mathfrak{I}^{-1}{H\left(\mu, v\right)}F_r\left(\mu, v\right)} \quad \left(20\right)
$$

则公式(18)可以表示为

$$
S\left(x, y\right)= H\left(\mu, v\right)+ r\left(\mu, v\right) \quad \left(21\right)
$$

$g(x, y)$ 是滤波后的期望增强图像。由于 $z(x, y)$ 是 $F(x, y)$ 的对数，因此可以通过应用以下方式生成 $g(x, y)$：

光照归一化过程包含两个步骤。第一步是通过改进的同态滤波对人脸图像进行处理，目的是消除光照影响。第二步是使用直方图均衡化来提高对比度。最终，结果图像的光照已成功实现归一化。框图方案如 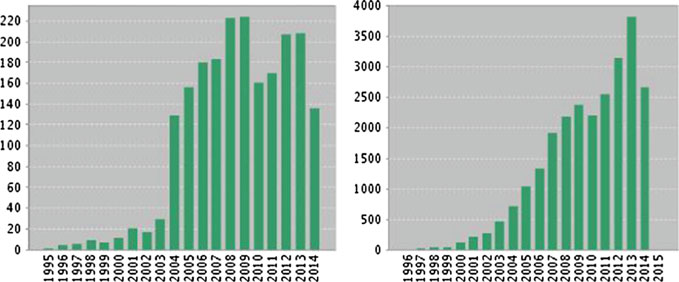(和)所示。

3 当前趋势

显示了从1995年至今光照滤波技术的发表和引用趋势，数据来源于Web of Science。光照技术的趋势保持平稳，而人脸识别的趋势则急剧上升。

4 比较

表1展示了光照滤波器的优缺点。

滤波器	优点	缺点
SSR	1. SSR的尺度扩大，其阴影稳定性质量元素展示	1. 包含辐射古老特性稀有特征
SSR	1. SSR的尺度扩大，其阴影稳定性质量元素展示	2. SSR 具有多样化的元素根据范围压力特性尺度。
SSR	1. SSR的尺度扩大，其阴影稳定性质量元素展示	3. SSR 的运行效果不佳音调执行
MSR	1. 对图像处理效果良好是灰度的	1. 为了增强图像的颜色，使用了直方图均衡化 这可能会导致颜色尺度变化，观察到图像颜色不平衡的情况可以是此结果
ASR	1. 更快地恢复图像同时保持执行实际上完全相同的迷人之处	1. 基本上扩展了
ASR	1. 更快地恢复图像同时保持执行实际上完全相同的迷人之处	2. 像素之间的微弱结果包含较少变化的
HOMO	1. 构成基础的部分针对这些低图像的重复出现情况亮度增强和高背光带有反射	1. 吸引人的离散元素相邻之间的角度可能不存在于产出中的离散尺度 发现于产量处
DCT	1. 该滤波器保持低 , mid 和高频的系数同时降低图像空间维度	1. 离散余弦变换没有足够的能量递归限制在鉴于这一事实，即通过大，它们超过的分布式时间
WA	1. 不需要训练图像这项技术。然而，他们无法消除产生的阴影完全是一个他们需要的角色在保护方面的多功能性不连续性充分	1. 这无法执行，因为有更多开发和更快的算法用于小波变化

(续)

滤波器	优点	缺点
各向同性	1. 可保护图像边缘同时可降低噪声同时	1. 对引入不敏感且具有对称性，导致模糊边缘
可操控的	1. 不同特定个体的外壳可以弄清楚如何帮助进行主体识别	1. 需要相当多的组件的度量
非局部的	1. 在以下层面工作预处理并揭示了一些基本的兴趣点，这些点使其成为更优选的勾勒时的选择 a 强人脸识别技术	1. 它的去噪能力较差在一致区域中
自适应 非局部	1. 按顺序应用此滤波以增强数据可能会被用于分割、弛豫测量或基于纤维追踪的或基于纤维追踪的应用	1. 该方法并未减少算法的麻烦，而仅仅略微降低了滤波的精确性
MODIFIED 各向异性	1. 过滤方法可能是一种机会被类似地安排作为一个单独的尺度空间通道此外，一些多尺度在不同领域的研究方法区域	1. 在这些上可能会更慢集合论的安排形态学原则
MODIFIED 各向异性	1. 过滤方法可能是一种机会被类似地安排作为一个单独的尺度空间通道此外，一些多尺度在不同领域的研究方法区域	2. 具有耗散特征包括模糊的不连续性
DOG	1. 无光源信息或需要3D形状数据滤波以及大量训练样本的数量。因此，此滤波器适用于训练每人单张图像的	1. 基于表面：利用空间空间信息
DOG	1. 无光源信息或需要3D形状数据滤波以及大量训练样本的数量。因此，此滤波器适用于训练每人单张图像的	2. 边缘连接：一种过量的分割
DOG	1. 无光源信息或需要3D形状数据滤波以及大量训练样本的数量。因此，此滤波器适用于训练每人单张图像的	3. 基于图像：仅有低层次特征

5 讨论

SSR被证明有助于减少光照差异，并显著保护类间区分性。与SSR相比，MSR方法在边缘支持方面表现更优，同时在渐进范围分层和对比度方面也取得更好的效果。然而，仍可观察到一些缺陷，如边缘和颜色失真。人脸图像的反射分量可通过同态滤波技术去除。空间域利用同态滤波，可显著实现高效的时间管理，并可随后开发出用于同态滤波的简单核。

在测量减少和通过特征图像生成增加类间差异的需求推动下，DCT策略得到了改进。基于小波的分解对图像进行图像分析，将其分解为估计系数和细节系数，分别对应图像的低频和高频分量图像。这种基于小波的图像分解将图像划分为估计系数和细节系数，分别对应图像的低频和高频部分。

最近引入了一种用于图像去噪的算法技术，即非局部均值或NL均值。NL均值不同于现有的去噪技术。该降噪任务会考虑整个图像的像素值。通过应用该算法技术，可以在图像的每个微小窗口中轻松找到相似窗口，从而用于图像的去噪目的。

结果表明，NL能够在无需明确噪声估计的情况下产生同样理想的结果，与非自适应形式的滤波相比，在处理平稳噪声时（在低噪声情况下会有一些提升）。除此之外，实际应用中发现，对于瑞利分布噪声以及空间贫乏高斯噪声，该方法的表现均优于以往的非自适应NL‐means滤波变体。

改进的各向异性算法的调整可能依赖于放射科医生对肝脏超声图像中医学细微元素所需变化的反馈。这些调整特别体现在使用大尺度模板进行导数、扩散以及拉普拉斯项的测量上。最终，通过引入正则化，将提高超声图像细微元素的清晰度。通过改进的同态滤波执行方式，高斯亮度中的对比度已基本降低。该调整可能已应用于本系统的核心部分，即高斯差（DoG）滤波，随后通过直方图均衡化增强对比度，最终提升图像质量。

6 结论

对于人脸识别所遇到的这些严峻挑战，研究人员需要采用一种全面的方法来应对模式识别中的光照变化，并且工作站视觉符合预期。需要帮助的是，不同的系统可能具备承受或补偿图像中由光照变化所引起差异的能力。最终，汤姆的阅读进展涉及光照的变化。总之，在人脸识别中解决光照问题仍然是一个巨大的挑战，这需要持续而巨大的努力。

以及对其的关注。在本研究中，进行了广泛的调查，涵盖了最新引入的最先进技术。