C/C++每日一练(20230308) 最大间距、被围绕的区域、天际线问题

原创已于 2023-07-28 22:42:07 修改 · 925 阅读

13 ·

CC 4.0 BY-SA版权

文章标签：

#c++ #算法 #数据结构

于 2023-03-08 10:00:00 首次发布

刷题专栏同时被 2 个专栏收录

632 篇文章

订阅专栏

C/C++每日一练

91 篇文章

订阅专栏

文章提供了三个编程题目，分别涉及找到无序数组排序后相邻元素的最大差值、填充被‘X’包围的区域以及计算建筑群的天际线轮廓。题目要求线性时间复杂度和空间复杂度的解决方案，并给出了C++的代码实现。

1. 最大间距 ★★★

2. 被围绕的区域 ★★

3. 天际线问题 ★★★

🌟 每日一练刷题专栏

C/C++ 每日一练专栏

Python 每日一练专栏

1. 最大间距

给定一个无序的数组，找出数组在排序之后，相邻元素之间最大的差值。

如果数组元素个数小于 2，则返回 0。

示例 1:

输入: [3,6,9,1]
输出: 3
解释: 排序后的数组是 [1,3,6,9], 其中相邻元素 (3,6) 和 (6,9) 之间都存在最大差值 3。

示例 2:

输入: [10]
输出: 0
解释: 数组元素个数小于 2，因此返回 0。

说明:

你可以假设数组中所有元素都是非负整数，且数值在 32 位有符号整数范围内。
请尝试在线性时间复杂度和空间复杂度的条件下解决此问题。

代码：

#include <bits/stdc++.h>
using namespace std;

class Solution
{
public:
    int maximumGap(vector<int> &nums)
    {
        set<int> st(nums.begin(), nums.end());
        int res = 0, pre = INT_MIN;
        for (auto iter = st.begin(); iter != st.end(); ++iter)
        {
            if (pre == INT_MIN)
            {
                pre = *iter;
                continue;
            }
            else
            {
                res = max(res, *iter - pre);
                pre = *iter;
            }
        }
        return res;
    }
};

int main()
{
	Solution s;
	vector<int> nums = {3,6,9,1};
	cout << s.maximumGap(nums) << endl;

	nums = {10};
	cout << s.maximumGap(nums) << endl;

	return 0;
}

输出：

3
0

2. 被围绕的区域

给你一个 m x n 的矩阵 board ，由若干字符 'X' 和 'O' ，找到所有被 'X' 围绕的区域，并将这些区域里所有的 'O' 用 'X' 填充。

示例 1：

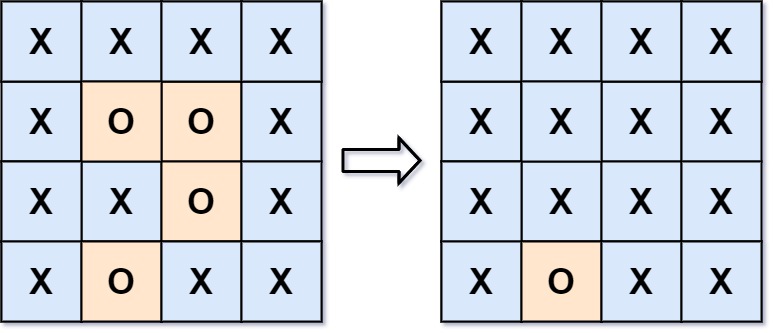
输入：board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
输出：[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
解释：被围绕的区间不会存在于边界上，换句话说，任何边界上的 'O' 都不会被填充为 'X'。 任何不在边界上，或不与边界上的 'O' 相连的 'O' 最终都会被填充为 'X'。如果两个元素在水平或垂直方向相邻，则称它们是“相连”的。

示例 2：

输入：board = [["X"]]
输出：[["X"]]

提示：

m == board.length
n == board[i].length
1 <= m, n <= 200
board[i][j] 为 'X' 或 'O'

代码：

#include <bits/stdc++.h>
using namespace std;

class Solution
{
public:
    int m, n;
    void solve(vector<vector<char>> &board)
    {
        m = board.size();
        if (!m)
            return;
        n = board[0].size();
        if (!n)
            return;
        for (int i = 0; i < m; ++i)
        {
            if (i == 0 || i == m - 1)
            {
                for (int j = 0; j < n; ++j)
                {
                    if (board[i][j] == 'O')
                        dfs(board, i, j);
                }
            }
            else
            {
                if (board[i][0] == 'O')
                    dfs(board, i, 0);
                if (board[i][n - 1] == 'O')
                    dfs(board, i, n - 1);
            }
        }
        for (int i = 0; i < m; ++i)
            for (int j = 0; j < n; ++j)
            {
                if (board[i][j] == 'A')
                    board[i][j] = 'O';
                else
                    board[i][j] = 'X';
            }
    }
    void dfs(vector<vector<char>> &board, int i, int j)
    {
        board[i][j] = 'A';
        if (i - 1 < m && i - 1 >= 0 && j < n && j >= 0 && board[i - 1][j] == 'O')
        {
            dfs(board, i - 1, j);
        }
        if (i + 1 < m && i + 1 >= 0 && j < n && j >= 0 && board[i + 1][j] == 'O')
        {
            dfs(board, i + 1, j);
        }
        if (i < m && i >= 0 && j - 1 < n && j - 1 >= 0 && board[i][j - 1] == 'O')
        {
            dfs(board, i, j - 1);
        }
        if (i < m && i >= 0 && j + 1 < n && j + 1 >= 0 && board[i][j + 1] == 'O')
        {
            dfs(board, i, j + 1);
        }
    }
};

int main()
{
	Solution s;
	vector<vector<char>> board = {
		{'X','X','X','X'},
		{'X','O','O','X'},
		{'X','X','O','X'},
		{'X','O','X','X'}
		};
	s.solve(board);
	for (auto res: board){
		for (auto c: res)
			cout << c;
		cout << endl;
	}

	return 0;
}

输出：

XXXX
XXXX
XXXX
XOXX

3. 天际线问题

城市的天际线是从远处观看该城市中所有建筑物形成的轮廓的外部轮廓。给你所有建筑物的位置和高度，请返回由这些建筑物形成的 天际线 。

每个建筑物的几何信息由数组 buildings 表示，其中三元组 buildings[i] = [lefti, righti, heighti] 表示：

lefti 是第 i 座建筑物左边缘的 x 坐标。
righti 是第 i 座建筑物右边缘的 x 坐标。
heighti 是第 i 座建筑物的高度。

天际线 应该表示为由 “关键点” 组成的列表，格式 [[x1,y1],[x2,y2],...] ，并按 x 坐标 进行排序。关键点是水平线段的左端点。列表中最后一个点是最右侧建筑物的终点，y 坐标始终为 0 ，仅用于标记天际线的终点。此外，任何两个相邻建筑物之间的地面都应被视为天际线轮廓的一部分。

注意：输出天际线中不得有连续的相同高度的水平线。例如 [...[2 3], [4 5], [7 5], [11 5], [12 7]...] 是不正确的答案；三条高度为 5 的线应该在最终输出中合并为一个：[...[2 3], [4 5], [12 7], ...]

示例 1：

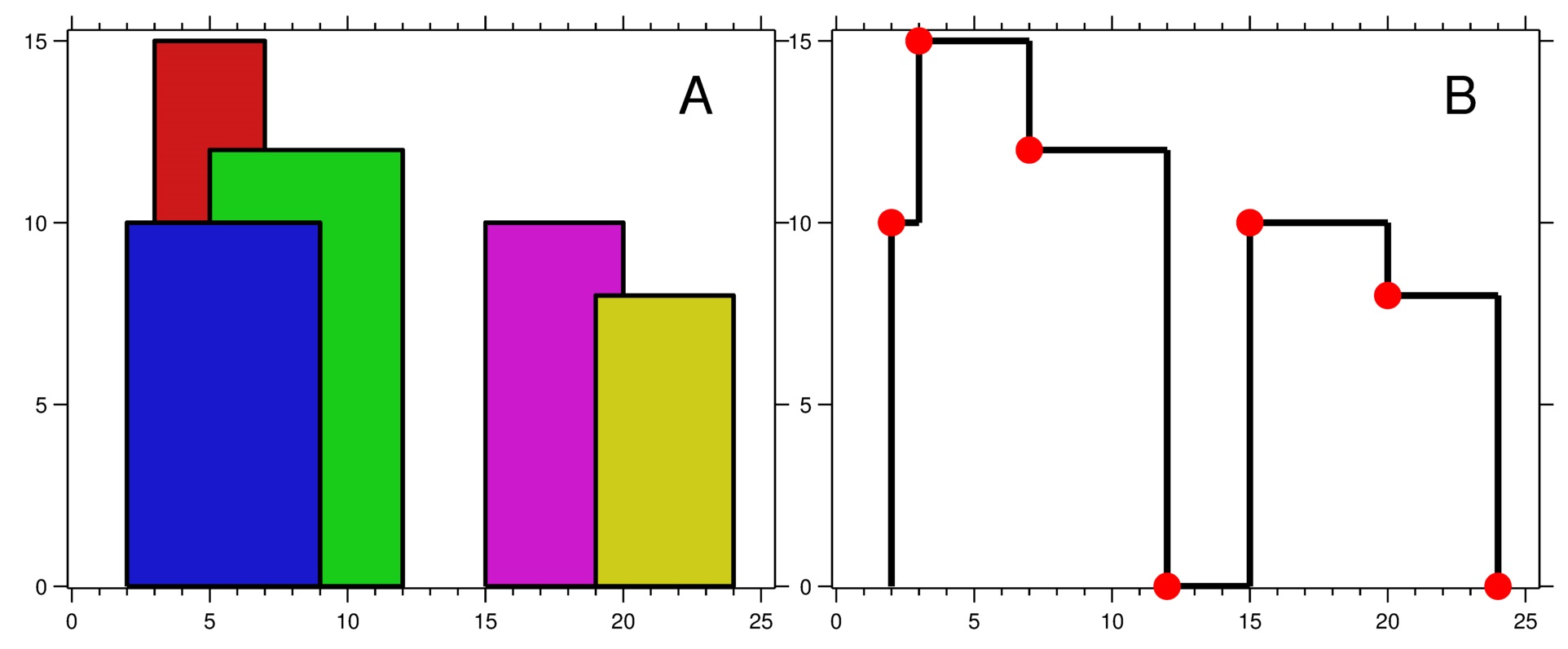
输入：buildings = [[2,9,10],[3,7,15],[5,12,12],[15,20,10],[19,24,8]]
输出：[[2,10],[3,15],[7,12],[12,0],[15,10],[20,8],[24,0]]
解释：
图 A 显示输入的所有建筑物的位置和高度，
图 B 显示由这些建筑物形成的天际线。图 B 中的红点表示输出列表中的关键点。

示例 2：

输入：buildings = [[0,2,3],[2,5,3]]
输出：[[0,3],[5,0]]

提示：

1 <= buildings.length <= 104
0 <= lefti < righti <= 2^31 - 1
1 <= heighti <= 2^31 - 1
buildings 按 lefti 非递减排序

代码：

#include <bits/stdc++.h>
using namespace std;

class Solution
{
public:
    vector<pair<int, int>> getSkyline(vector<vector<int>> &buildings)
    {
        vector<pair<int, int>> h, res;
        multiset<int> m;
        int pre = 0, cur = 0;
        for (auto &a : buildings)
        {
            h.push_back({a[0], -a[2]});
            h.push_back({a[1], a[2]});
        }
        sort(h.begin(), h.end());
        m.insert(0);
        for (auto &a : h)
        {
            if (a.second < 0)
                m.insert(-a.second);
            else
                m.erase(m.find(a.second));
            cur = *m.rbegin();
            if (cur != pre)
            {
                res.push_back({a.first, cur});
                pre = cur;
            }
        }
        return res;
    }
};

int main()
{
	Solution s;
	vector<vector<int>> buildings = {{2,9,10},{3,7,15},{5,12,12},{15,20,10},{19,24,8}};
	vector<pair<int, int>> vect = s.getSkyline(buildings);
	int i = 0;
	cout << "[[";
	for (auto pair: vect){
		cout << pair.first << "," << pair.second;
		cout << (++i < vect.size() ? "],[" : "]]\n");
	}

	i = 0, buildings = {{0,2,3},{2,5,3}};
	vect = s.getSkyline(buildings);
	cout << "[[";
	for (auto pair: vect){
		cout << pair.first << "," << pair.second;
		cout << (++i < vect.size() ? "],[" : "]]");
	}

	return 0;
}

输出：

[[2,10],[3,15],[7,12],[12,0],[15,10],[20,8],[24,0]]
[[0,3],[5,0]]