C/C++每日一练(20230220) 用字母组成图形、子集II、路径总和II

原创已于 2023-07-28 23:07:33 修改 · 1.9k 阅读

3 ·

CC 4.0 BY-SA版权

文章标签：

#数据结构 #算法 #二叉树 #backtrack #dfs

于 2023-02-20 19:44:33 首次发布

刷题专栏同时被 2 个专栏收录

632 篇文章

订阅专栏

C/C++每日一练

91 篇文章

订阅专栏

文章包含了三个编程题目：1)利用字母组成图形，通过给定的行数和列数生成图形；2)子集II，要求返回整数数组的所有不重复子集；3)二叉树路径总和II，找到所有从根节点到叶子节点且路径和为目标值的路径。解决方案涉及到深度优先搜索和广度优先搜索算法的应用。

1. 利用字母组成图形

利用字母可以组成一些美丽的图形，下面给出了一个例子：

ABCDEFG
BABCDEF
CBABCDE
DCBABCD
EDCBABC

这是一个5行7列的图形，请找出这个图形的规律，并输出一个n行m列的图形。
输入一行，包含两个整数n和m，分别表示你要输出的图形的行数的列数。

代码：

#include <stdio.h>
#include <math.h>
int main()
{
    int m, n;
    scanf("%d%d", &n, &m);
    int i, j;
    for (i = 0; i < n; i++)
    {
        for (j = 0; j < m; j++)
        {
            printf("%c", 65 + abs(i - j));
        }
        printf("\n");
    }
    return 0;
}

输入输出：

5
7
ABCDEFG
BABCDEF
CBABCDE
DCBABCD
EDCBABC

--------------------------------
Process exited after 3.645 seconds with return value 0
请按任意键继续. . .

2. 子集 II

给你一个整数数组 nums ，其中可能包含重复元素，请你返回该数组所有可能的子集（幂集）。

解集不能包含重复的子集。返回的解集中，子集可以按 任意顺序 排列。

示例 1：

输入：nums = [1,2,2]
输出：[[],[1],[1,2],[1,2,2],[2],[2,2]]

示例 2：

输入：nums = [0]
输出：[[],[0]]

提示：

1 <= nums.length <= 10
-10 <= nums[i] <= 10

代码：

#include <bits/stdc++.h>
using namespace std;
class Solution
{
public:
	vector<vector<int>> subsetsWithDup(vector<int> &nums)
	{
		vector<vector<int>> res;
		sort(nums.begin(), nums.end());
		dfs(nums, 0, res);
		return res;
	}
private:
	vector<int> stack;
	void dfs(vector<int> &nums, int start, vector<vector<int>> &res)
	{
		res.push_back(stack);
		int last = INT_MIN;
		for (int i = start; i < nums.size(); i++)
		{
			if (last != nums[i])
			{
				stack.push_back(nums[i]);
				dfs(nums, i+1, res);
				stack.pop_back();
			}
			last = nums[i];
		}
	}
};

3. 二叉树路径总和 II

给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。

叶子节点 是指没有子节点的节点。

示例 1：

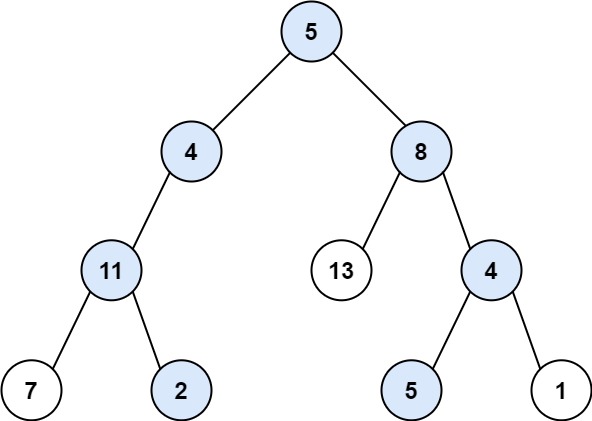
输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：[[5,4,11,2],[5,8,4,5]]

示例 2：

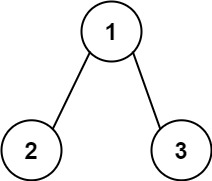
输入：root = [1,2,3], targetSum = 5
输出：[]

示例 3：

输入：root = [1,2], targetSum = 0
输出：[]

提示：

树中节点总数在范围 [0, 5000] 内
-1000 <= Node.val <= 1000
-1000 <= targetSum <= 1000

代码：

#include <bits/stdc++.h>
using namespace std;

struct TreeNode
{
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

class Solution
{
public:
    vector<vector<int>> pathSum(TreeNode *root, int sum)
    {
        vector<vector<int>> res;
        vector<int> track;
        backTrack(root, res, track, sum);
        return res;
    }
    void backTrack(TreeNode *root, vector<vector<int>> &res, vector<int> track, int sum)
    {
        if (!root)
        {
            return;
        }
        if (!root->left && !root->right)
        {
            sum -= root->val;
            track.push_back(root->val);
            if (sum == 0)
            {
                res.push_back(track);
            }
            track.pop_back();
            sum += root->val;
            return;
        }
        sum -= root->val;
        track.push_back(root->val);
        backTrack(root->left, res, track, sum);
        backTrack(root->right, res, track, sum);
        track.pop_back();
        sum += root->val;
    }
};

代码2：DFS

class Solution {
public:
    int ans = INT_MIN;
    int maxPathSum(TreeNode* root) {
        dfs(root);
        return ans;
    }
    int dfs(TreeNode *root){
        if(!root) return 0;
        int left = dfs(root->left);
        int right = dfs(root->right);
        ans = max(ans,left+root->val + right);
        return max(0,root->val+max(left,right));
    }
};

附录

深度优先搜索算法

Depth-First-Search，DFS
是一种用于遍历或搜索树或图的算法。这个算法会尽可能深的搜索树的分支。当节点v的所在边都己被探寻过，搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点，则选择其中一个作为源节点并重复以上过程，整个进程反复进行直到所有节点都被访问为止。

广度优先搜索算法

Breadth-First Search，BFS
又译作宽度优先搜索，或横向优先搜索，是一种图形搜索算法。简单的说，BFS是从根节点开始，沿着树的宽度遍历树的节点。如果所有节点均被访问，则算法中止。

BFS 和 DFS 的区别

1 数据结构
bfs 遍历节点是先进先出，一般使用队列作为辅助数据结构
dfs遍历节点是先进后出，一般使用栈作为辅助数据结构

2 访问节点的方式
bfs是按层次访问的，先访问源点，再访问它的所有相邻节点，并且标记结点已访问，根据每个邻居结点的访问顺序，依次访问它们的邻居结点，并且标记节点已访问，重复这个过程，一直访问到目标节点或无未访问的节点为止。
dfs 是按照一个路径一直访问到底，当前节点没有未访问的邻居节点时，然后回溯到上一个节点，不断的尝试，直到访问到目标节点或所有节点都已访问。

3 应用
bfs 适用于求源点与目标节点距离近的情况，例如：求最短路径。
dfs 更适合于求解一个任意符合方案中的一个或者遍历所有情况，例如：全排列、拓扑排序、求到达某一点的任意一条路径。