算法(Algorithm)
代表着用系统的方法描述解决问题的策略机制,可以通过一定规范的 输入,在有限时间内获得所需要的 输出。
一个算法的好坏是通过 时间复杂度 与 空间复杂度 来衡量的。就是代码需要的时间和内存,也就你时间成本和空间成本。其实这个一个动态的调整,到一定程度,往往就是用空间去换取时间,或者去时间去换取空间(dp其实就是在用空间去换取时间)。当然优秀的代码就是很优秀,排序也是这样,他们的目标都是把一堆数字进行排序。
常见时间复杂度的 “大O表示法” 描述有以下几种:
时间复杂度 非正式术语 O(1) 常数阶 O(n) 线性阶 O(n2) 平方阶 O(log n) 对数阶 O(n log n) 线性对数阶 O(n3) 立方阶 O(2n) 指数阶 一个算法在N规模下所消耗的时间消耗从大到小如下:
O(1) < O(log n) < O(n) < O(n log n) < O(n2) < O(n3) < O(2n)
常见的排序算法
根据时间复杂度的不同,常见的算法可以分为3大类。
1.O(n²) 的排序算法
冒泡排序
选择排序
插入排序
2.O(nlogn) 的排序算法
堆排序
希尔排序 //O(nlog²n) ~ 最坏时O(n²)
归并排序 //O(nlogn) ~ 最坏时O(nlog²n)
快速排序 //O(nlogn) ~ 最坏时O(n²)
3.线性O(n)的排序算法
桶排序
计数排序 //O(n+m)
基数排序 //O(kn) ~ 最坏时O(n²)
以下代码对C++算法库<algorithm>里的Sort()函数,进行排序用时测试,排列1亿个随机整数居然只用34秒,1000万个数只用2.6秒。
#include <iostream>
#include <cstdlib>
#include <ctime>
#include <array>
#include <algorithm>
using namespace std;
int main(void)
{
const unsigned int num = 100000000;
static array <int,num> arr;
clock_t tClock;
srand(time(NULL)+rand());
cout<<"随机生成"<<arr.size()<<"个"<<arr.size()<<"以内的整数:"<<endl;
tClock = clock();
for_each(arr.begin(),arr.end(),[](int &i)->void{i=rand()%arr.size();});
tClock = clock() - tClock;
cout<<"随机赋值"<<num<<"个整数共耗时:"<< tClock <<"毫秒"<<endl;
cout<<"\n<algorithm>库算法Sort()排序:"<<endl;
tClock = clock();
sort(arr.begin(),arr.end());
//reverse(arr.begin(),arr.end()); //再倒序即成降序;倒序百万个数只要10毫秒左右
tClock = clock() - tClock;
cout<<"库函数排序"<<num<<"个整数耗时:"<< tClock <<"毫秒"<<endl;
return 0;
}
/*
排序 1亿个 整数的测试结果:
随机生成100000000个100000000以内的整数:
随机赋值100000000个整数共耗时:2656毫秒
<algorithm>库算法Sort()排序:
库函数排序100000000个整数耗时:34411毫秒
--------------------------------
Process exited after 37.98 seconds with return value 0
请按任意键继续. . .
*/
/*
排序1000万个数的测试结果:
随机生成10000000个10000000以内的整数:
随机赋值10000000个整数共耗时:265毫秒
<algorithm>库算法Sort()排序:
库函数排序10000000个整数耗时:3074毫秒
--------------------------------
Process exited after 4.106 seconds with return value 0
请按任意键继续. . .
*/
把num值降至100000,sort()与其他排序法的耗时对比:
#include <iostream>
#include <cstdlib>
#include <ctime>
#include <array>
#include <algorithm>
using namespace std;
int main(void)
{
const unsigned int num = 100000;
static array <int,num> arr,tmp;
clock_t tClock;
srand(time(NULL)+rand());
cout<<"随机生成"<<tmp.size()<<"个"<<tmp.size()<<"以内的整数:"<<endl;
tClock = clock();
for_each(tmp.begin(),tmp.end(),[](int &i)->void{i=rand()%tmp.size();});
tClock = clock() - tClock;
cout<<"随机赋值"<<num<<"个整数共耗时:"<< tClock <<"毫秒"<<endl;
if (num<=500) for (auto a:tmp) cout<<a<<"\t";
cout<<"\n冒泡排序 Bubble Sort:"<<endl;
for (int i=0;i<num;i++) arr.at(i)=tmp.at(i);
tClock = clock();
for(int i=0;i<arr.size();i++)
for(int j=1;j<arr.size()-i;++j)
if(arr.at(j-1)>arr.at(j)) swap(arr.at(j-1),arr.at(j));
tClock = clock() - tClock;
if (num<=500){
cout<<"排序后:"<<endl;
for (auto a:arr) cout<<a<<"\t";
cout<<endl;
}
cout<<"冒泡排序"<<num<<"个整数耗时:"<< tClock <<"毫秒"<<endl;
cout<<"\n选择排序 Selection Sort:"<<endl;
for (int i=0;i<num;i++) arr.at(i)=tmp.at(i);
tClock = clock();
for (int i=0,min;i<arr.size()-1;i++){
min = i;
for (int j=i+1;j<arr.size();j++)
if (arr.at(j)<arr.at(min)) min=j;
swap(arr.at(i),arr.at(min));
}
tClock = clock() - tClock;
if (num<=500){
cout<<"排序后:"<<endl;
for (auto a:arr) cout<<a<<"\t";
cout<<endl;
}
cout<<"选择排序"<<num<<"个整数耗时:"<< tClock <<"毫秒"<<endl;
cout<<"\n插入排序 Insertion Sort:"<<endl;
for (int i=0;i<num;i++) arr.at(i)=tmp.at(i);
tClock = clock();
for (int i=0,j,tmp;i<arr.size()-1;i++){
j = i;
tmp = arr.at(i+1);
while (j>=0 && arr.at(j)>tmp) arr.at(j+1) = arr.at(j--);
arr.at(j+1) = tmp;
}
tClock = clock() - tClock;
if (num<=500){
cout<<"排序后:"<<endl;
for (auto a:arr) cout<<a<<"\t";
cout<<endl;
}
cout<<"插入排序"<<num<<"个整数耗时:"<< tClock <<"毫秒"<<endl;
cout<<"\n<algorithm>库算法Sort()排序:"<<endl;
for (int i=0;i<num;i++) arr.at(i)=tmp.at(i);
tClock = clock();
sort(arr.begin(),arr.end());
tClock = clock() - tClock;
if (num<=500){
cout<<"排序后:"<<endl;
for (auto a:arr) cout<<a<<"\t";
cout<<endl;
}
cout<<"库函数排序"<<num<<"个整数耗时:"<< tClock <<"毫秒"<<endl;
return 0;
}
测试结果:真可谓秒杀啊
//第1次测试结果:
随机生成100000个100000以内的整数:
随机赋值100000个整数共耗时:2毫秒
冒泡排序 Bubble Sort:
冒泡排序100000个整数耗时:152607毫秒
选择排序 Selection Sort:
选择排序100000个整数耗时:72822毫秒
插入排序 Insertion Sort:
插入排序100000个整数耗时:45840毫秒
<algorithm>库算法Sort()排序:
库函数排序100000个整数耗时:28毫秒
--------------------------------
Process exited after 272.1 seconds with return value 0
请按任意键继续. . .
//第2次测试结果:
随机生成100000个100000以内的整数:
随机赋值100000个整数共耗时:3毫秒
冒泡排序 Bubble Sort:
冒泡排序100000个整数耗时:151895毫秒
选择排序 Selection Sort:
选择排序100000个整数耗时:73151毫秒
插入排序 Insertion Sort:
插入排序100000个整数耗时:46617毫秒
<algorithm>库算法Sort()排序:
库函数排序100000个整数耗时:25毫秒
--------------------------------
Process exited after 272.6 seconds with return value 0
请按任意键继续. . .
//第3次测试结果:
随机生成100000个100000以内的整数:
随机赋值100000个整数共耗时:3毫秒
冒泡排序 Bubble Sort:
冒泡排序100000个整数耗时:151941毫秒
选择排序 Selection Sort:
选择排序100000个整数耗时:72759毫秒
插入排序 Insertion Sort:
插入排序100000个整数耗时:45291毫秒
<algorithm>库算法Sort()排序:
库函数排序100000个整数耗时:25毫秒
--------------------------------
Process exited after 270.8 seconds with return value 0
请按任意键继续. . .
如果用冒泡排序1亿个数,估计至少得算上2天2夜吧。但在网上看到sort()是基于快速排序的,那n/logn=1250万倍,这样算冒泡法排1亿个数岂不得用86小时???
关于sort()具体怎么实现的呢? 据说它的算法是快速排序、归并排序等各种排序方法的综合体。
附录:几种排序法的图示
Bubble Sort

Insertion Sort
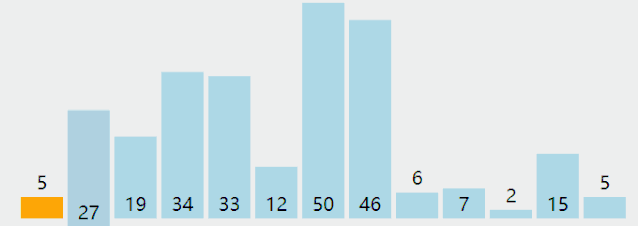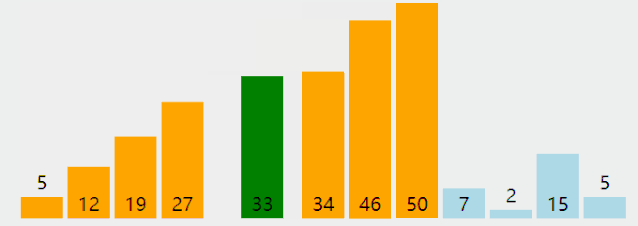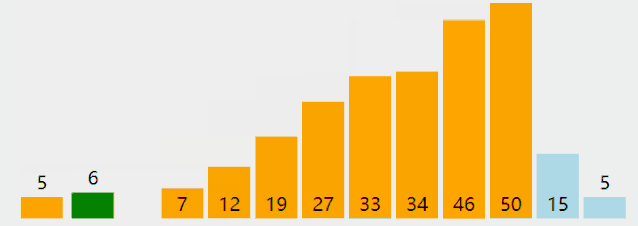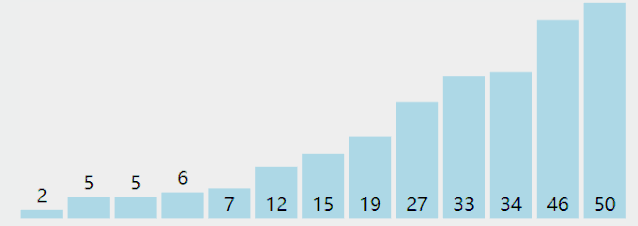
Selection Sort

Quick Sort
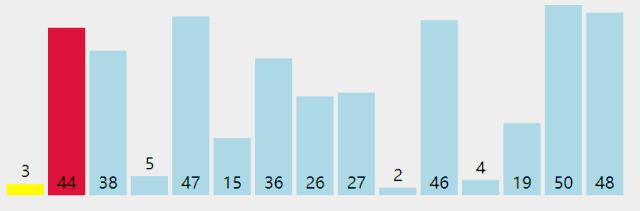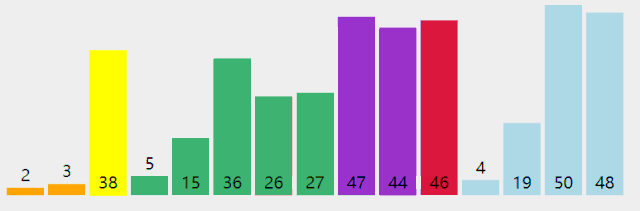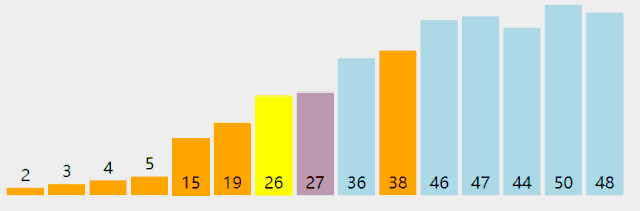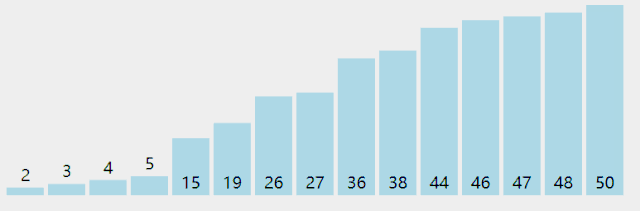
Merge Sort
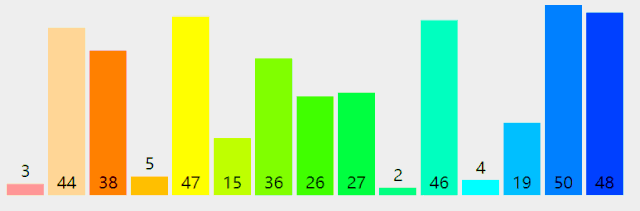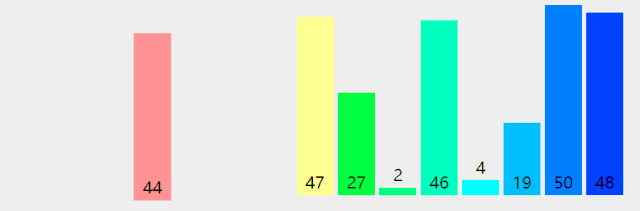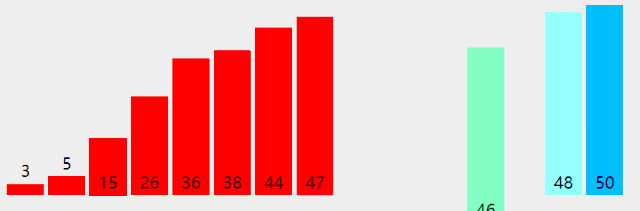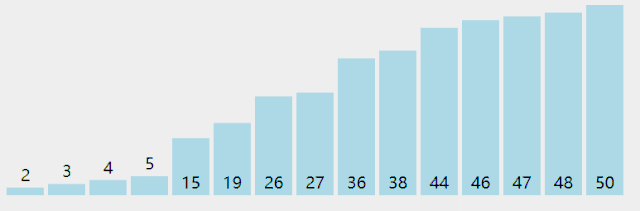





 本文探讨了算法的时间复杂度和空间复杂度,重点介绍了不同排序算法的时间复杂度,如冒泡排序、选择排序、插入排序等,并通过C++代码展示了标准库Sort()函数对大量数据的高效排序能力,比较了其与其他简单排序算法的性能差异。测试结果显示Sort()函数在处理大规模数据时具有显著优势。
本文探讨了算法的时间复杂度和空间复杂度,重点介绍了不同排序算法的时间复杂度,如冒泡排序、选择排序、插入排序等,并通过C++代码展示了标准库Sort()函数对大量数据的高效排序能力,比较了其与其他简单排序算法的性能差异。测试结果显示Sort()函数在处理大规模数据时具有显著优势。

















 3903
3903

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










