Java算法之归并排序

       这里我们说说归并排序，其最坏的时间维度是O(NlogN)，其思想是利用了“分治法”。

       所谓的“分治法”即为：当一个大问题难以解决时，我们将其分为若干个小问题，然后将这些小问题解决了，那么大问题也就顺利解决了。那么怎么将其具体于排序上面呢？分两步：(1)拆分；(2)合并。

       (1)拆分

       当一组数据没法排序时，我们将其一分为二，发现他的一半还是没法排序，再将其一分为二，以此类推，直到分到只剩下一个元素为止，这样就好排序了，如下：

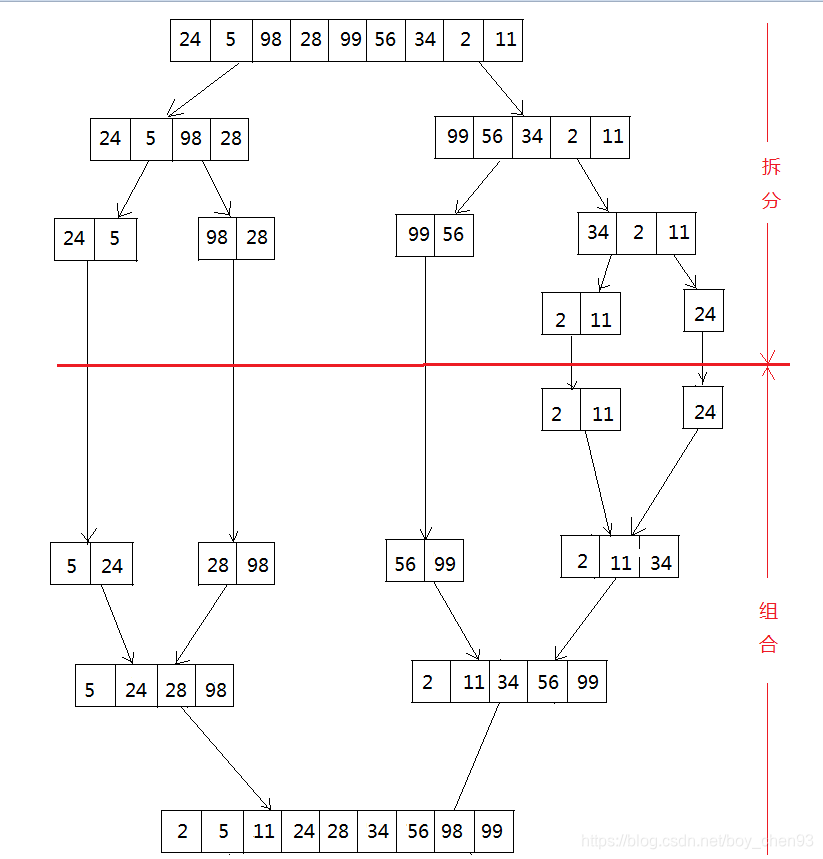
       (2)组合

       经过上述步骤，我们得到两组有序数组，在就是如何将这两组有序数组结合为一组有序数组，就ok了，不知道大家打过牌没有，假如有两副牌，他们都是从牌顶到牌底从小到大有序的，那我们如何将其组合成一副有序的牌组呢？我们先从两副牌顶各摸一张牌，并比较其大小，将小的放在手中，在以此类推，那么手中的牌就是这两副牌的有序数组了。

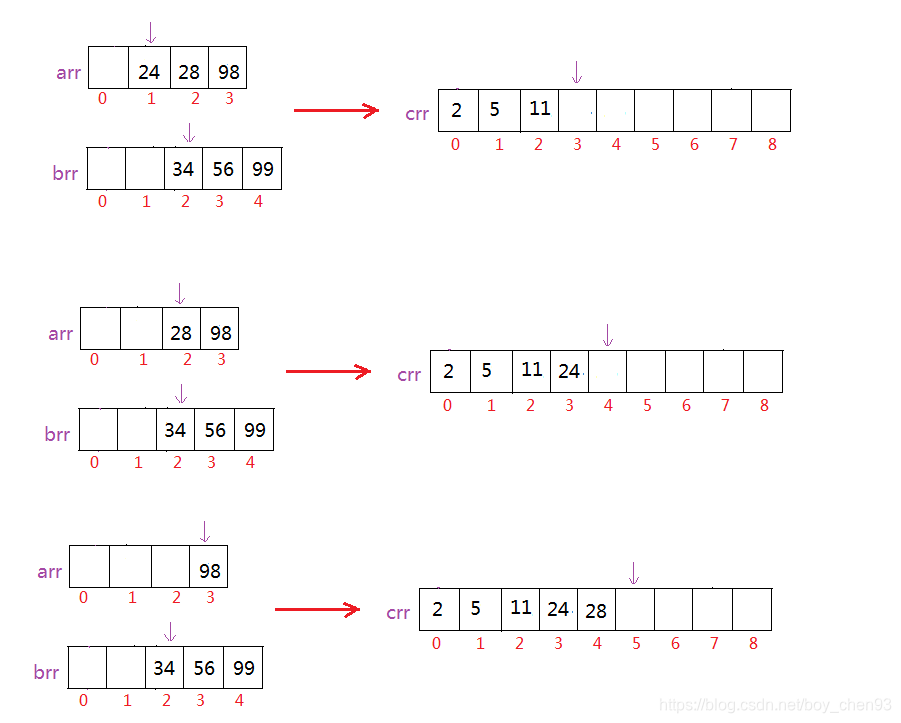
       比如说，我们需要将上述最后两组数排序位一组有序数组：

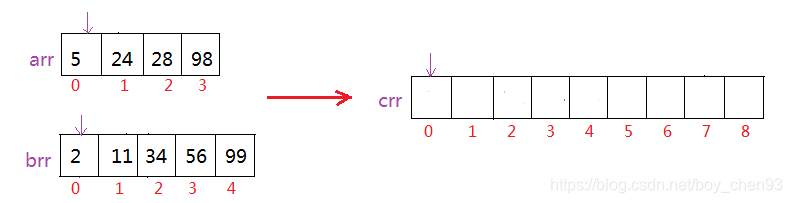
 首先比较arr[0]和brr[0]，arr[0]>brr[0]，那么我们将brr[0]的值放在crr[0]处：

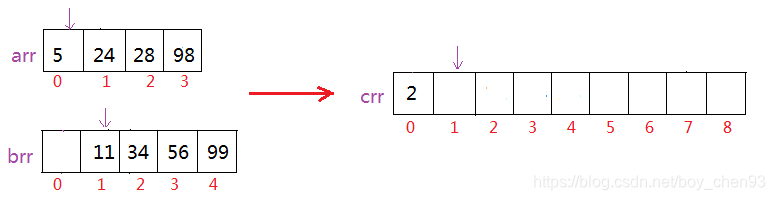
再比较arr[0]和brr[1]，发现brr[1]>arr[0]，那么我们将arr[0]放在crr[1]处：

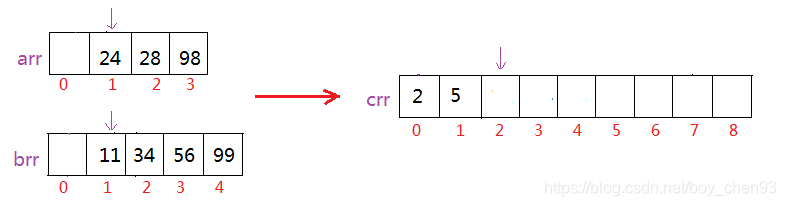
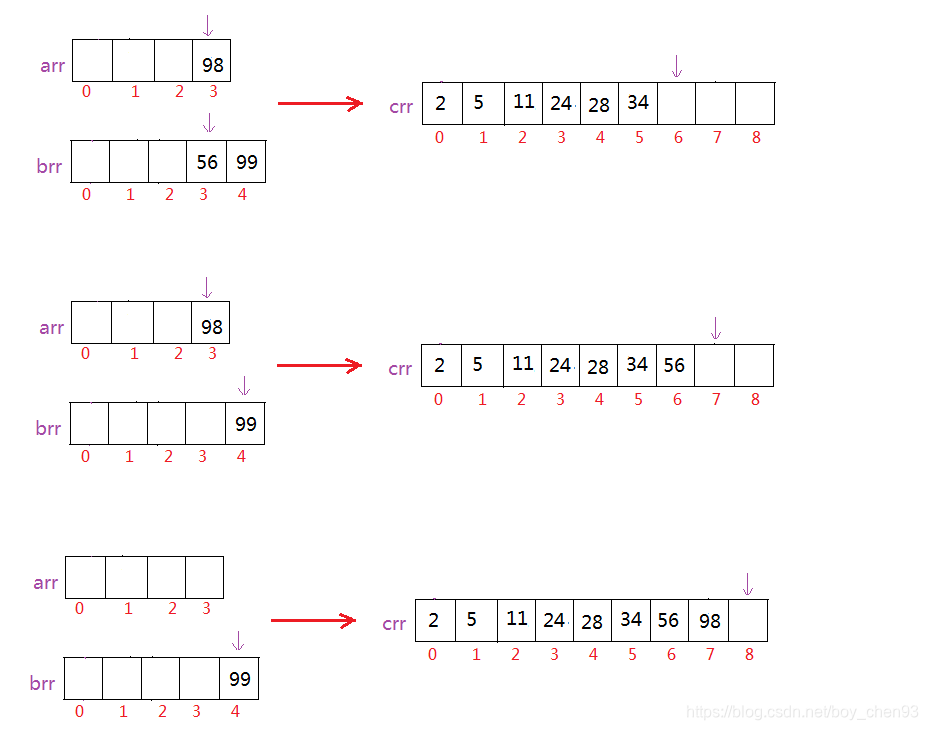
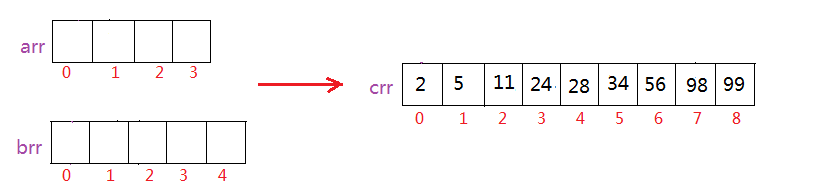
后面，以此类推：

 

 

       下面用代码实现上述逻辑：

package com.Jevin.priorityQueue;

import java.util.Arrays;

public class MergerSort {

    public static void main(String[] args) {
        int[] arr = {24, 5, 98, 28, 99, 56, 34, 2 ,11};
        MergeSort(arr);
        System.out.print(Arrays.toString(arr));
    }

    private static void MergeSort(int[] arr) {
        Sort(arr, 0, arr.length - 1);
    }

    /**
     * 拆分
     * @param a
     * @param left
     * @param right
     */
    private static void Sort(int[] a, int left, int right) {
        if(left>=right) {
            return;
        }
        int mid = (left + right) / 2;
        //二路归并排序里面有两个Sort，多路归并排序里面写多个Sort就可以了
        Sort(a, left, mid);
        Sort(a, mid + 1, right);
        merge(a, left, mid, right);
    }

    /**
     * 合并
     * @param a
     * @param left
     * @param mid
     * @param right
     */
    private static void merge(int[] a, int left, int mid, int right) {
        int[] tmp = new int[a.length];
        int r1 = mid + 1;
        int tIndex = left;
        int cIndex=left;
        // 逐个归并
        while(left <=mid && r1 <= right) {
            if (a[left] <= a[r1])
                tmp[tIndex++] = a[left++];
            else
                tmp[tIndex++] = a[r1++];
        }
        // 将左边剩余的归并
        while (left <=mid) {
            tmp[tIndex++] = a[left++];
        }
        // 将右边剩余的归并
        while ( r1 <= right ) {
            tmp[tIndex++] = a[r1++];
        }
        //将左右归并
        while(cIndex<=right){
            a[cIndex]=tmp[cIndex];
            cIndex++;
        }
    }
}

OK！！！