「小杜」机器学习践行鹿-3-为什么要发明决策树

前言
书接上篇,这一篇讲讲决策树的起承转合。
我们知道机器学习就是让机器像人类一样通过经验去解决问题,那么,问题来了
我们人类是怎么通过经验解决问题的呢?
题外话:说原理容易,这写代码也太难了叭
Tags:机器学习
文章目录
🎫 啥是决策树
“什么样的人看起来让人信任?”
当我们被问到这个问题的时候,你的想法首先是什么呢,当我们逐渐长大,对这个问题可能有自己的标准:
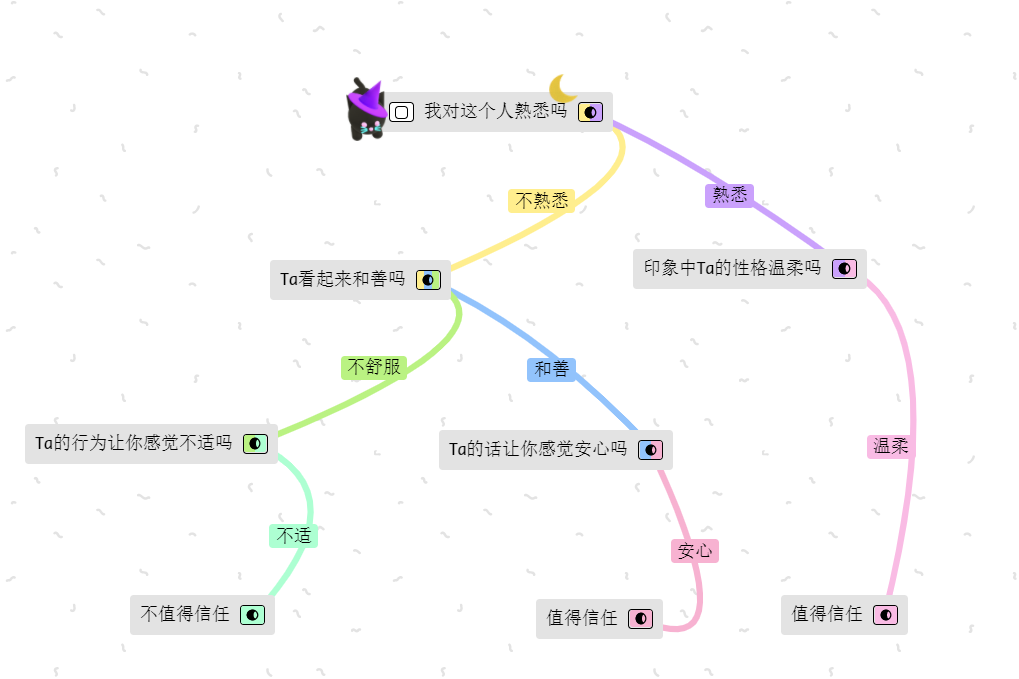
“爷爷奶奶阅历丰富”让人信任,“性格温柔博学多识”也让人又安心感,我们通常对更加熟悉的人有信任感,长得好看的人也是
画一幅不标准的图可能是这个样~
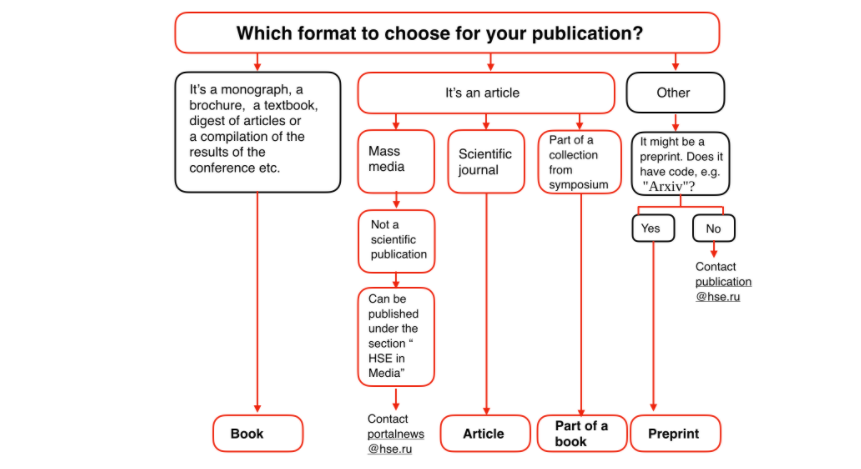
就像俄罗斯国立高等经济研究大学(Higher School of Economics)提供的关于「如何在学院网站上发表论文」的流程图一样,我们很可能是这样思考的,像一个树状图一样。
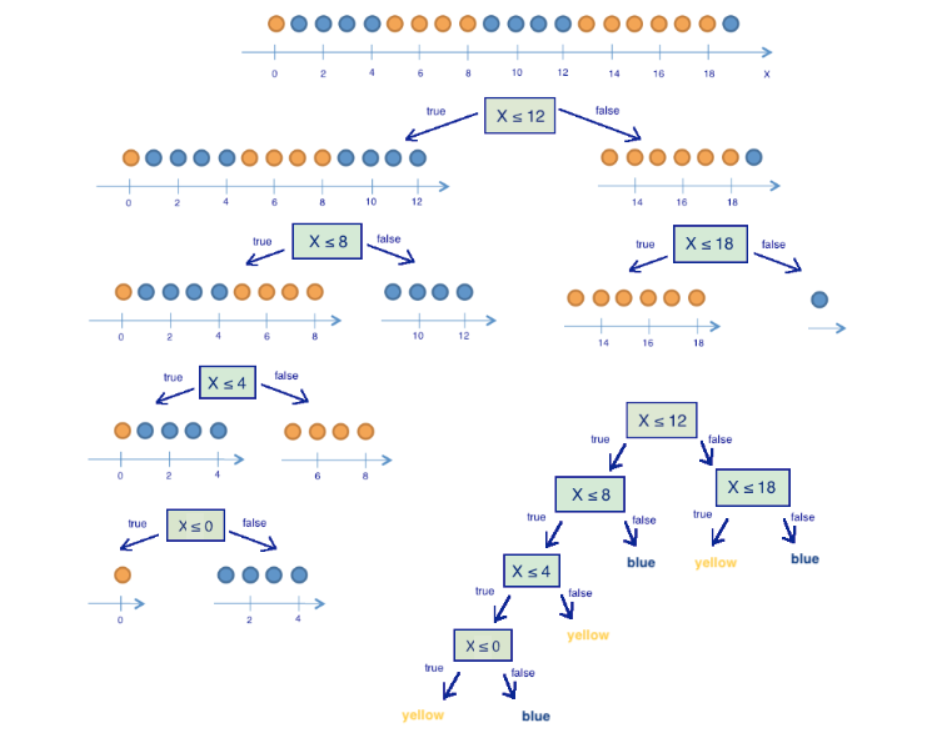
🌈 怎样构建一颗决策树
构建决策树的流行算法有很多,比如说ID3或者C4.5,那我们具体是怎么去划分每一颗树杈的呢,性格、年龄、熟悉程度,这么多特征我们最看重哪个呢?
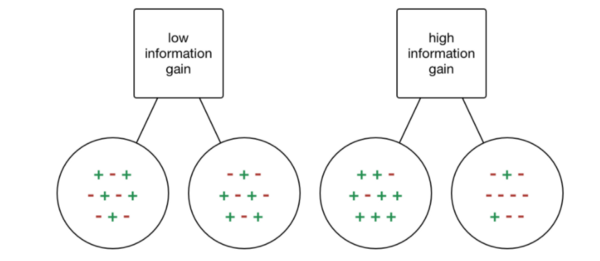
为了解决以上问题,这里需要介绍一下熵、条件熵、信息增益、信息增益比的概念
熵(Entropy)
用规范的话来说就是表示一个随机变量的复杂性或者不确定性
这是一个在物理、信息论和其他领域中广泛应用的重要概念,可以衡量获得的信息量。对于具有 N 种可能状态的系统而言,熵的定义如下:
S
=
−
∑
i
=
1
N
p
i
log
2
p
i
S = -\sum_{i=1}^{N}p_i \log_2{p_i}
S=−i=1∑Npilog2pi
其中,
p
i
p_i
pi 是系统位于第
i
i
i个状态的概率。熵可以描述为系统的混沌程度,熵越高,系统的有序性越差,反之亦然。熵将帮助我们高效的分割数据。
也就是说,经过分割数据后,熵下降的越多,说明系统的有序性越高,更容易得到正确的分类。
比如说,在网上买书,只知道书名,书的质量对于我来说是不确定的,那么就可以假设它的信息熵为10
条件熵(Conditional Entropy)
条件熵就是说表示在知道某一个条件之后,某一随机变量的复杂性或者不确定性
还是买书的例子
我在网上看到了豆瓣的评价,之后,书的质量更加确定了,它的信息熵就下降为6
这就是条件熵
信息增益(Info-Gain)
什么是信息增益呢,就是说表示在知道某一个条件之后,某一随机变量的不确定性的减少量
还是拿买书的例子说
在我知道豆瓣的评价之后,我对书的质量更加了解了,不确定性(熵)下降了4,
表示我获得了熵为4的信息增益,这就叫做信息增益
信息增益比(Gain-ratio)
为什么又谈到信息增益比呢,它的意思是信息增益与某一变量的熵的比值
在买书的例子中,我们把书分为
质量好、质量坏两种,每本书是一个离散值(不可能出现0.5本书),数据是离散数据但是有的例子是连续数据,比如身高、体重、年龄、距离等等,或者说没有明显的类别区分
假设这样的问题,如果只考虑信息增益的话,算法会偏向于把每一个不重复的数据自成一类,极端情况下每个叶子节点只有一个样本,最后树的形状就会是一棵庞大且深度很浅的树,这样的划分是极为不合理的。虽然信息熵降到了最低但是并不具备实用性。
所以在算法中可以考虑使用信息增益比
题外话:像ID3算法就是使用了**信息增益**,C4.5算法使用了**信息增益比**
评判分割好坏的指标
对于之前提到的问题:“什么样的人看起来让人信任?”
它的初始的不确定性(熵)是确定的,在决策树中,我们要做的就是通过不断的分割,每次分割都按照一定的标准,最终实现回答问题。
分割的标准一般还用到以下指标:
-
信息增益(IG): I G ( Q ) = S O − ∑ i = 1 q N i N S i IG(Q) = S_O - \sum_{i=1}^{q}\frac{N_i}{N}S_i IG(Q)=SO−∑i=1qNNiSi
-
基尼不确定性(Gini uncertainty): G = 1 − ∑ k ( p k ) 2 G = 1 - \sum\limits_k (p_k)^2 G=1−k∑(pk)2
(不纯度) -
错分率(Misclassification error): E = 1 − max k p k E = 1 - \max\limits_k p_k E=1−kmaxpk
实践中几乎不使用错分率,基尼不确定性和信息增益的效果差不多
构建一个决策树算法
ID3算法
ID3算法就是一个非常简单粗暴的算法。
假设我们是一家二手书店老板,有各种各样一大堆书(看都看不完),要给货架上重新摆放,质量好的放前面,质量差的放后面(也就是说是二分类:质量好和质量差)。
我们已经知道这堆书的一些特征:损坏程度(99新和非99新)、流行程度(流行和小众)、是否可珍藏(绝版和有再版)
-
此时我们就有一个根节点:一大堆书
-
选择特征:计算各种特征的信息增益 ,选择信息增益最大的特征,分类完数量大的那一摞书为单节点树
-
在子节点中选择特征:递归重复以上步骤
-
最终返回所有子树
有兴趣可以瞅瞅《统计学习方法》的伪代码,当然,随着决策树的不断发展,现在还有新的算法出现(下面会提到)
🌙 机器学习中的决策树
归纳和剪枝
了解了决策树的算法,我们来看看机器学习中怎样创建决策树模型,可以分为两个步骤:归纳和剪枝
归纳
归纳就是我们实际构建树的方法,比如说通过ID3、C4.5、CART算法来生成树的方法
-
从根节点出发,包含所有的训练样本
-
选择特征,把根节点划分为一个个子集
-
递归上述划分子集及产生叶节点的过程,这样每一个子集都会产生一个决策(子)树,直到所有节点变成叶节点
递归停止条件:
- 一个节点中所有的样本均为同一类别
- 没有特征可以用来对该节点样本进行划分
(attribute_list=null) - 没有样本能满足剩余特征的取值
剪枝
由于数据噪声的影响,生成的决策树可能存在过拟合的现象。剪枝就是说通过统计学的方法删除不可靠的分支,使得整个决策树的分类速度和分类精度得到提高。
下图就是对一个过拟合的决策树的可视化图像:
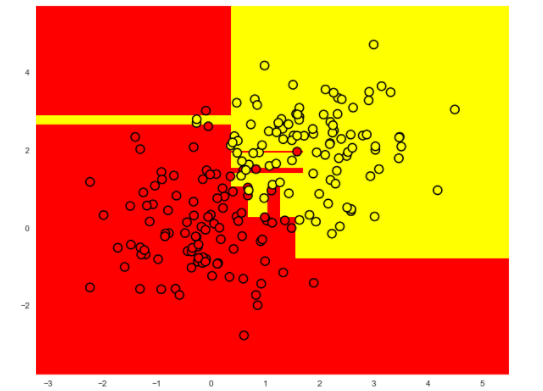
剪枝的方法可以分为预剪枝和后剪枝两种方法:
-
预剪枝:边建立决策树边进行剪枝的操作(更实用)

-
后剪枝:当建立完决策树后来进行剪枝操作

决策树可视化
这个是大佬写的,我还在琢磨中
from sklearn.tree import DecisionTreeClassifier
# 编写一个辅助函数,返回之后的可视化网格
def get_grid(data):
x_min, x_max = data[:, 0].min() - 1, data[:, 0].max() + 1
y_min, y_max = data[:, 1].min() - 1, data[:, 1].max() + 1
return np.meshgrid(np.arange(x_min, x_max, 0.01), np.arange(y_min, y_max, 0.01))
# max_depth参数限制决策树的深度
clf_tree = DecisionTreeClassifier(criterion='entropy', max_depth=3,
random_state=17)
# 训练决策树
clf_tree.fit(train_data, train_labels)
# 可视化
xx, yy = get_grid(train_data)
predicted = clf_tree.predict(np.c_[xx.ravel(),
yy.ravel()]).reshape(xx.shape)
plt.pcolormesh(xx, yy, predicted, cmap='autumn')
plt.scatter(train_data[:, 0], train_data[:, 1], c=train_labels, s=100,
cmap='autumn', edgecolors='black', linewidth=1.5)
结果如图:
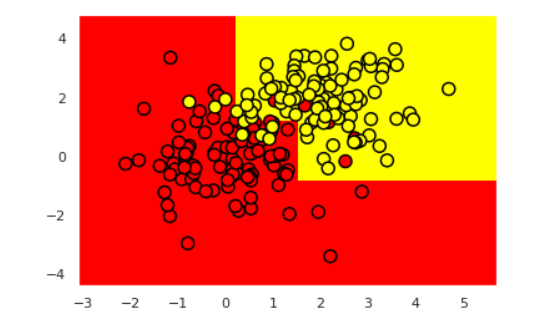
from ipywidgets import Image
from io import StringIO
import pydotplus
from sklearn.tree import export_graphviz
dot_data = StringIO()
export_graphviz(clf_tree, feature_names=['x1', 'x2'],
out_file=dot_data, filled=True)
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
Image(value=graph.create_png())
结果如图:
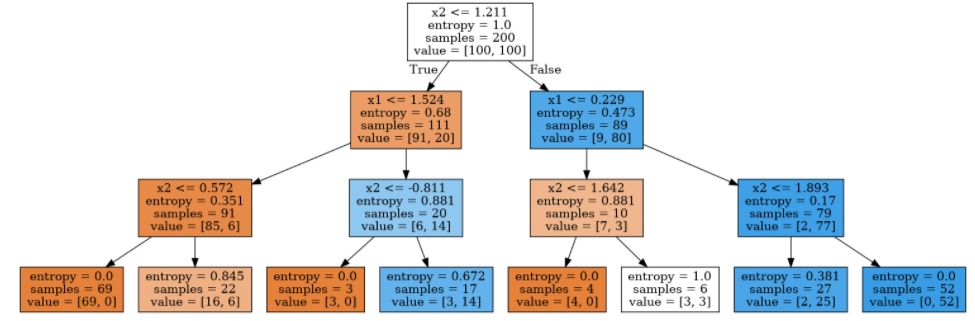
可以看到,数据被分为了2类,第一类的样本越多,橙色越深,第二类样本越多,蓝色越深。
🏓 决策树算法的优缺点
优点
- 易理解,机理解释简单
- 可用于小数据集
- 时间复杂度小
- 可以处理数字与数据的类别
- 可以处理多输出问题
- 对缺失值不敏感
- 可以处理不相关特征数据
- 效率高:一次构建,反复使用
缺点
- 对连续性的字段比较难预测
- 容易出现过拟合
- 当类别太多时,错误可能会增加的比较快
- 在处理特征关联性比较强的数据时,表现的不太好
- 对于各类样本不一致的数据,信息增益的结构偏向于那些具有更多数据的特征





 本文探讨了决策树的起源,通过解释熵、条件熵、信息增益等概念,阐述了如何构建决策树。介绍了ID3算法,并讨论了机器学习中的决策树归纳和剪枝过程,以及决策树的优缺点。
本文探讨了决策树的起源,通过解释熵、条件熵、信息增益等概念,阐述了如何构建决策树。介绍了ID3算法,并讨论了机器学习中的决策树归纳和剪枝过程,以及决策树的优缺点。
















 3551
3551

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








