缺失的第一个正整数——原地哈希

题目说明

这个是牛客101题中的第53题，题目描述是给一个无重复元素的数组，找出没有出现的最小的正整数

缺失的第一个正整数_牛客题霸_牛客网 

乍一看似乎不太难，但是要做到时间复杂度O(n)也是要花点心思的

思路详解

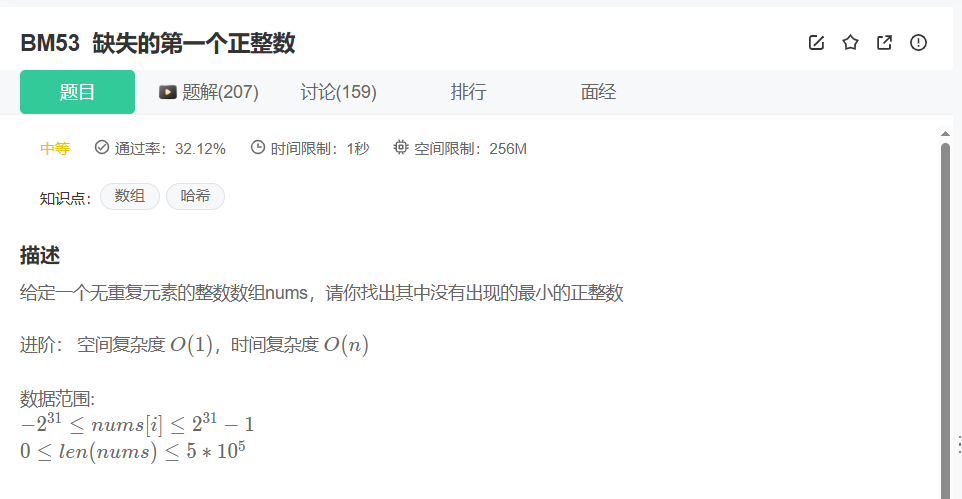
假设这有一个数组

题目要求的时间复杂度是O(n)，空间复杂度O(1)，就说明了只能在数组上原地操作了

首先，题目要求的是正整数，就排除了负数和0，已知最小的正整数是1，那么我们就可以在刚开始定义一个布尔类型的值，用来判断数组中是否出现1，如果并没有出现那就直接返回1

然后小于0或者大于数组长度的数也根本不符合要求，这时可以再遍历一遍数组，将这些数做特殊处理都赋值为1；

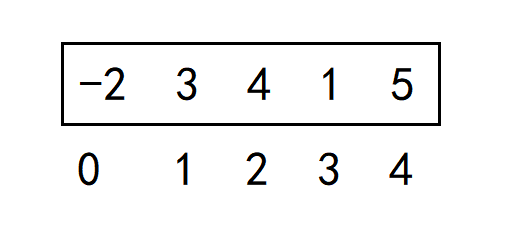
接着，就到了这个思路核心的地方了，原地哈希

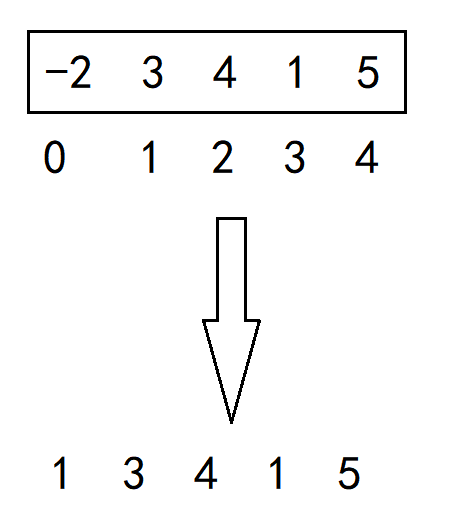
因为正整数是从1开始的，而下标是从0开始的，所以当当前循环的下标大于0时，取出当前下标对应的数 X ，将数组中 X-1 位置对应的数  取绝对值再取反（这里就是防止前面取反过了然后再取反变成正数）而且因为刚开始已经把负数处理了，所以当赋值相反数时都会将整数变为负数

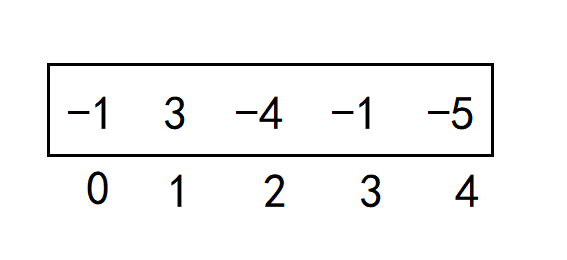
最后，再遍历一遍数组，找到的第一个正数所对应的下标加1就是数组中缺失的最小正整数

    int minNumberDisappeared(vector<int>& nums) {
        int n=nums.size();
        //首先定义布尔变量，然后遍历数组，判断数组中是否存在1
        bool flag = false;
        for (int num : nums) {
            if (num == 1) flag = true;
        }
        if (!flag) return 1;
        //接着排除掉不可能是题目要求的值
        //注意这里的引用
        for (int& num : nums) {
            if (num < 0 || num > n) num = 1;
        }
        //然后到核心部分，原地哈希，找出真正缺失的最小正整数
       for (int i = 0; i < n; i++) {
            int num = abs(nums[i]);
            nums[num - 1] = -abs(nums[num - 1]);
        }
        //最后一个for找出目标值
        for (int i = 0; i < n; i++) {
            if (nums[i] > 0) return i + 1;
        }
        return n+1;
    }