一二维前缀和/差分详解_一维前缀和数组 `pref` 中,`pref[i]` 表示的是:-优快云博客

本文链接：https://blog.youkuaiyun.com/bit_pan/article/details/148496461

引言

在刷算法题时，我们少不了会遇到求数组中某个区间的和以及重复修改某个区间的值。前者对应的是前缀和，后者对应的是差分。至于为什么要用前缀和或者差分，答案是显而易见的——暴力处理会导致超时。写这篇博客的主要原因是我自己在刷题时，首先刷的前缀和，其次是差分，但是刷到二维差分的时候，似乎掉进了某个思维的陷阱之中，突然就有很多疑问，才后知后觉是对前缀和与差分的理解不够，或者说这两者没区分清楚。于是在网上搜寻了一些博客，但是都没有让我豁然开朗。可能每个人疑惑的点不尽相同，或者说大多数博客都是把前缀和与差分分开介绍的，没有形成很直观的对比，所以我就写下了这篇博客，把前缀和与差分放在一起介绍，同时分享自己遇到的困惑，希望能够帮到和我一样的道友。至于怎么介绍这两种类型的算法，我的打算是理论与实践相结合，每一种类型提供一道对应的算法题。好了，废话不多说，下面进入正题！

一维前缀和

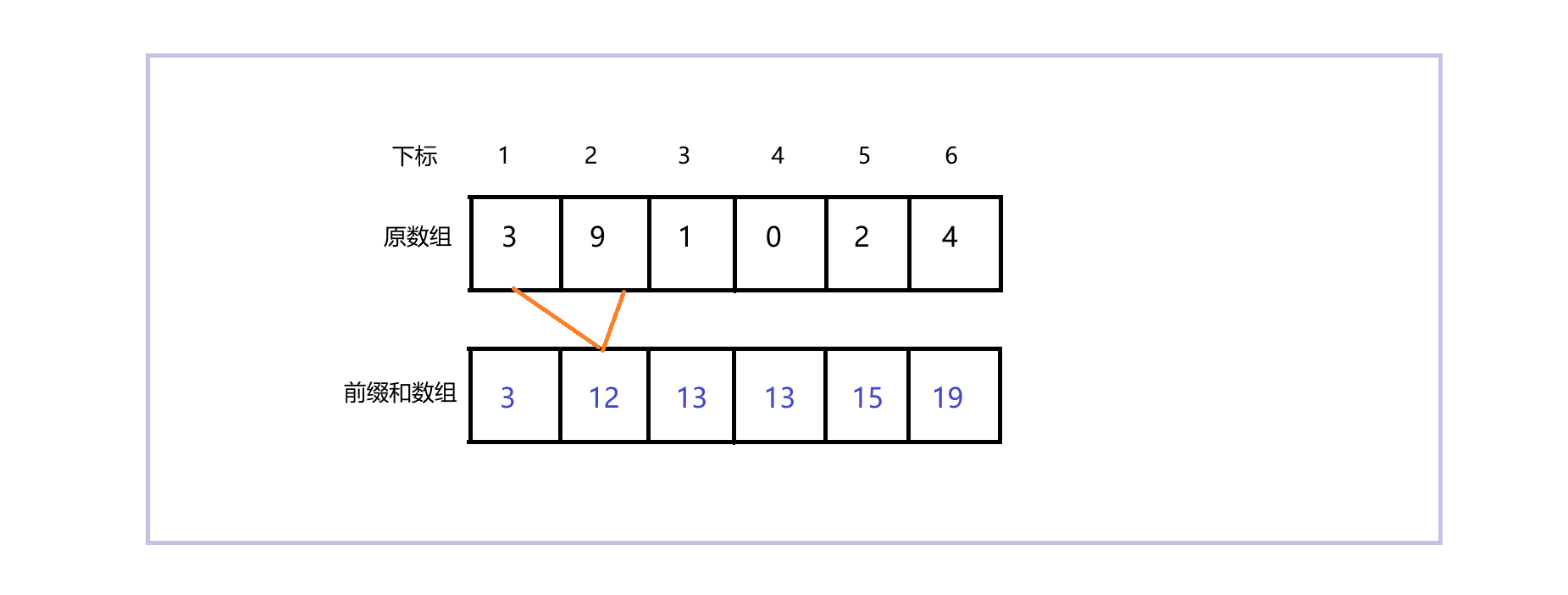
前缀和数组 f[ i ] = f[ i - 1] + a[ i ]（f为前缀和数组，a为原数组）。其中，f[ i ]表示：区间[1, i]中所有元素的和。可以看到，此处的下标是从1开始的，好处就是在通过前面公式构造前缀和数组时，不会导致越界。也不用特殊处理下标为1的位置，因为f[0] = 0，加上不影响。比如要求区间 [2, 5]的和，如果用暴力解法，自然就是遍历一遍，如果用前缀和数组，区间 [2, 5]的和 = f[ 5 ] - f[ 1 ]（下图中的绿色线段 - 橙色线段）。

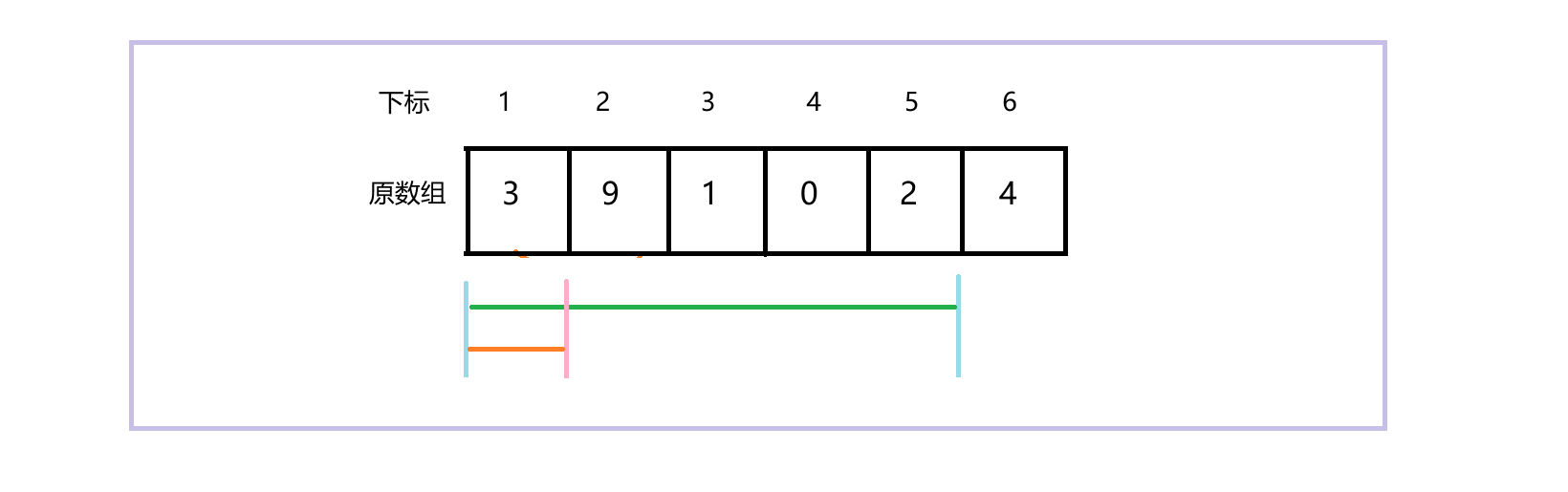
所以，某个区间的和 sum[ L ][ R ] = f[ R ] - f[ L - 1]。

下面来练练手：一维前缀和练习题

代码：

#include <iostream>
#include <vector>
using namespace std;

typedef long long ll;
const int N = 1e5 + 10;
ll a[N], f[N];

int main()
{
    ll n, m;
    cin >> n >> m;
    //下标从1开始
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
        f[i] = f[i - 1] + a[i];
    }
    /*第二种构建差分数组的方法：不需要存储原数组，节省了空间
    for (int i = 1; i <= n; i++) {
        int val;
        cin >> val;
        f[i] = f[i - 1] + val;
    }
    */
    while (m --) {
        int l, r;
        cin >> l >> r;
        cout << f[r] - f[l - 1] << endl;
    }
    return 0;
}

在上述代码中，构造前缀和数组的方法一共两种。第一种：存储原数组。第二种：不存储原数组。如果后续用不到原数组那么选择第二种构建方式可以在一定程度上节省空间。

二维前缀和

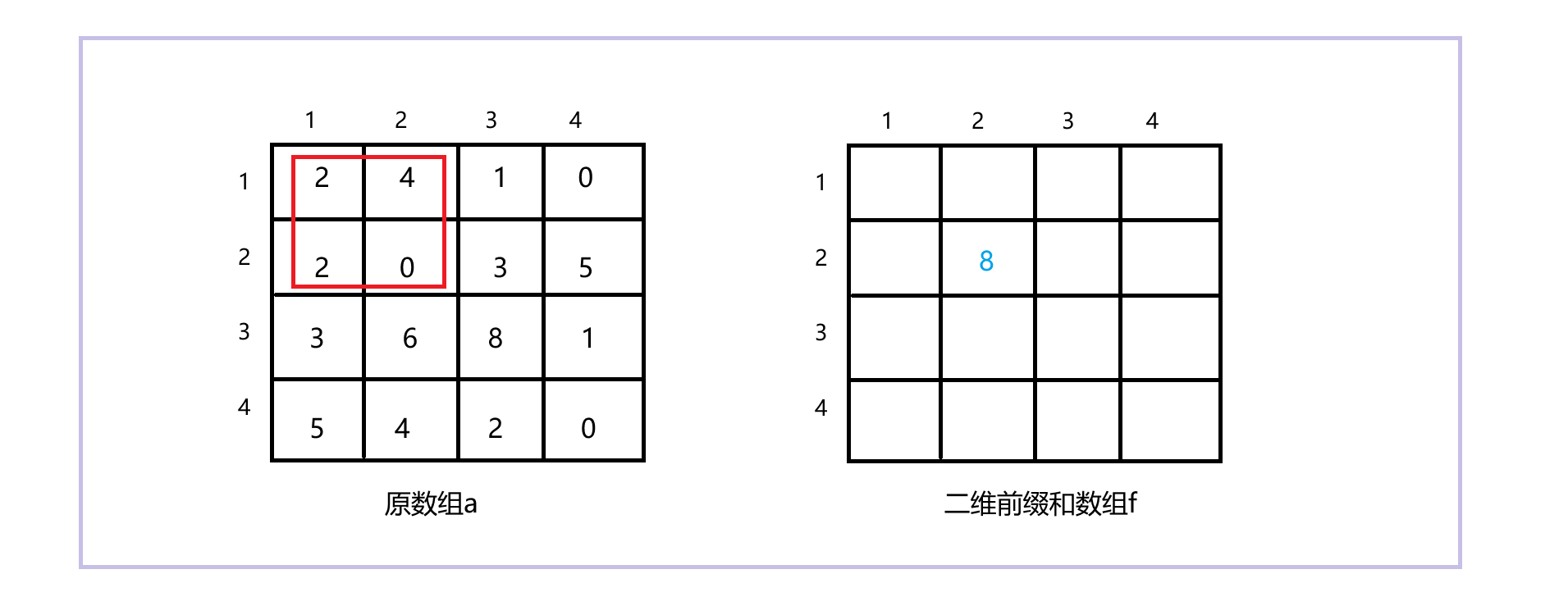
通过上图，解释一下f[ i ][ j ] 的含义：在原数组中，以（1,1）为左上角，以（i，j）为右下角的矩阵中，所有元素的和。比如上图的 f[2][2]，就是原数组中被框起来的矩阵中所有元素的和。这里的下标依然是从1开始，目的也是为了防止越界。知道了f[ i ][ j ] 的含义后，下面我们看看如何通过原数组构建二维前缀和数组。

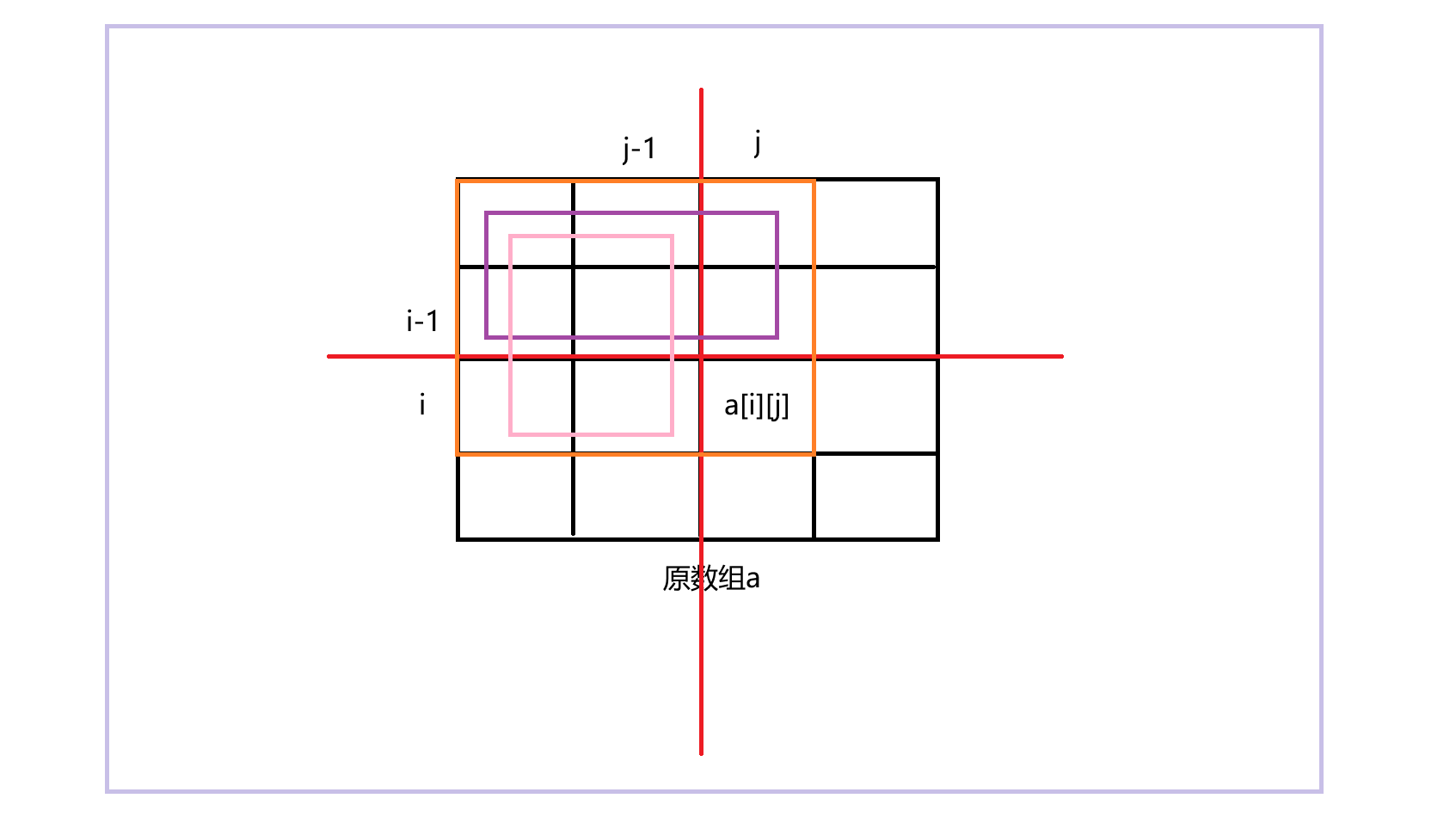
先说明一下，这个图看起来比较花，因为初衷就是为了帮组道友解决疑惑，尽可能详细会比较好理解，下面的解释对着图看就不迷了。

为了初始化二维前缀和数组中的f[i][j]，根据f[i][j]的含义：以（1,1）为左上角，以（i，j）为右下角的矩阵中所有元素的和。即上图中的橙色矩阵，要求该矩阵中所有元素的和，类似于求该矩阵的面积。紫色矩阵中所有元素的和 + 粉色矩阵中所有元素的和 + a[i][j] - 紫色矩阵与粉色矩阵交叉的部分（因为这部分被加了两次）即可得到橙色矩阵中所有元素的和。

如何求紫色矩阵和粉色矩阵中所有元素的和？遍历吗？

首先回答，不需要遍历。我们只需要想办法将这两个矩阵中所有元素的和给表示出来即可。回归到二维前缀和数组中每个元素的含义，紫色矩阵中所有元素的和可以用 f[ i - 1 ][ j ]来表示，粉色矩阵中所有元素的和可以用 f[ i ] [ j - 1]来表示。

所以橙色矩阵中所有元素的和 f[ i ][ j ] = f[ i - 1 ][ j ] + f[ i ][ j - 1] - f[ i - 1][ j - 1 ] + a[ i ][ j ]。利用此公式，即可构建出整个二维前缀和数组。

现在，我们是知道如何构建二维前缀和数组了，但是，题目要我们求的可不都是以（1,1）为左上角，以（i，j）为右下角的矩阵中所有元素的和呀，而是以（x1, y1）为左上角，以（x2, y2）为右下角的矩阵中所有元素的和。比如这题：二维前缀和模版题（下面会给出代码）。怎么求？

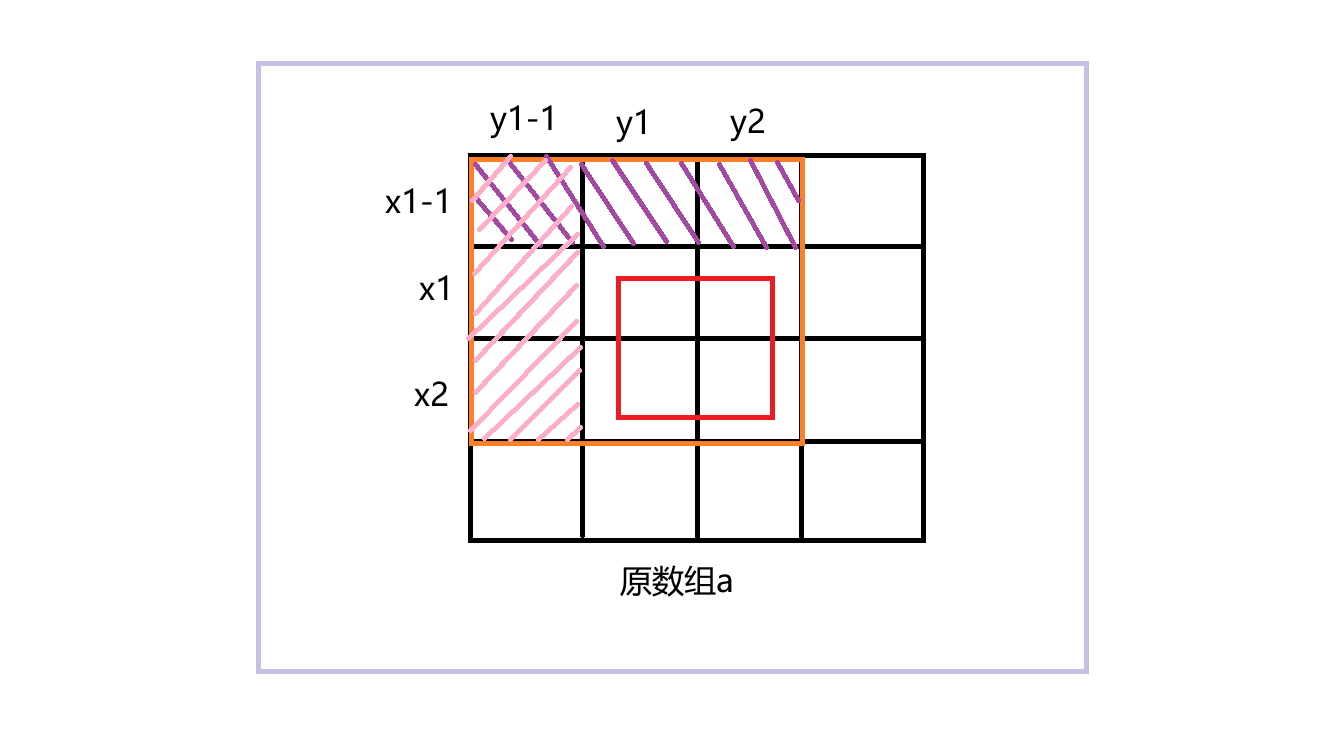
如上图，红色矩阵就是以（x1, y1）为左上角，以（x2, y2）为右下角的矩阵。要求红色矩阵中所有元素的和，用橙色矩阵中所有元素的和 - 紫色矩阵中所有元素的和 - 粉色矩阵中所有元素的和 + 粉色与紫色矩阵交叉的部分（被减了两次）。别忘了，走到这一步，我们已经手握一个二维前缀和数组了。橙色矩阵中所有元素的和 ---> f[x2][y2]，紫色矩阵中所有元素的和 ---> f[x1-1][y2]，粉色矩阵中所有元素的和 ---> f[x2][y1-1]，粉色与紫色矩阵交叉的部分 ---> f[x1-1][y1-1]。

所以，求任意矩阵中所有元素的和的公式为：target = f[x2][y2] - f[x1-1][y2] - f[x2][y1-1] + f[x1-1][y1-1]。

通过以上的学习，我们就已经具备了解决前面给出的算法题的能力了。题目链接：二维前缀和模版题。代码：

#include <iostream>
using namespace std;

typedef long long LL;
const int N = 1010;
LL f[N][N];//二维前缀和数组

int main()
{
    int n, m, q;
    cin >> n >> m >> q;
    //不需要存储原数组
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            LL val;
            cin >> val;
            //套公式
            f[i][j] = f[i - 1][j] + f[i][j - 1] - f[i - 1][j - 1] + val;
        }
    }
    while (q--) {
        LL x1, y1, x2, y2;
        cin >> x1 >> y1 >> x2 >> y2;
        //套公式
        LL ans = f[x2][y2] - f[x1 - 1][y2] - f[x2][y1 - 1] + f[x1 - 1][y1 - 1];
        cout << ans << endl;
    }
    return 0;
}

一维差分

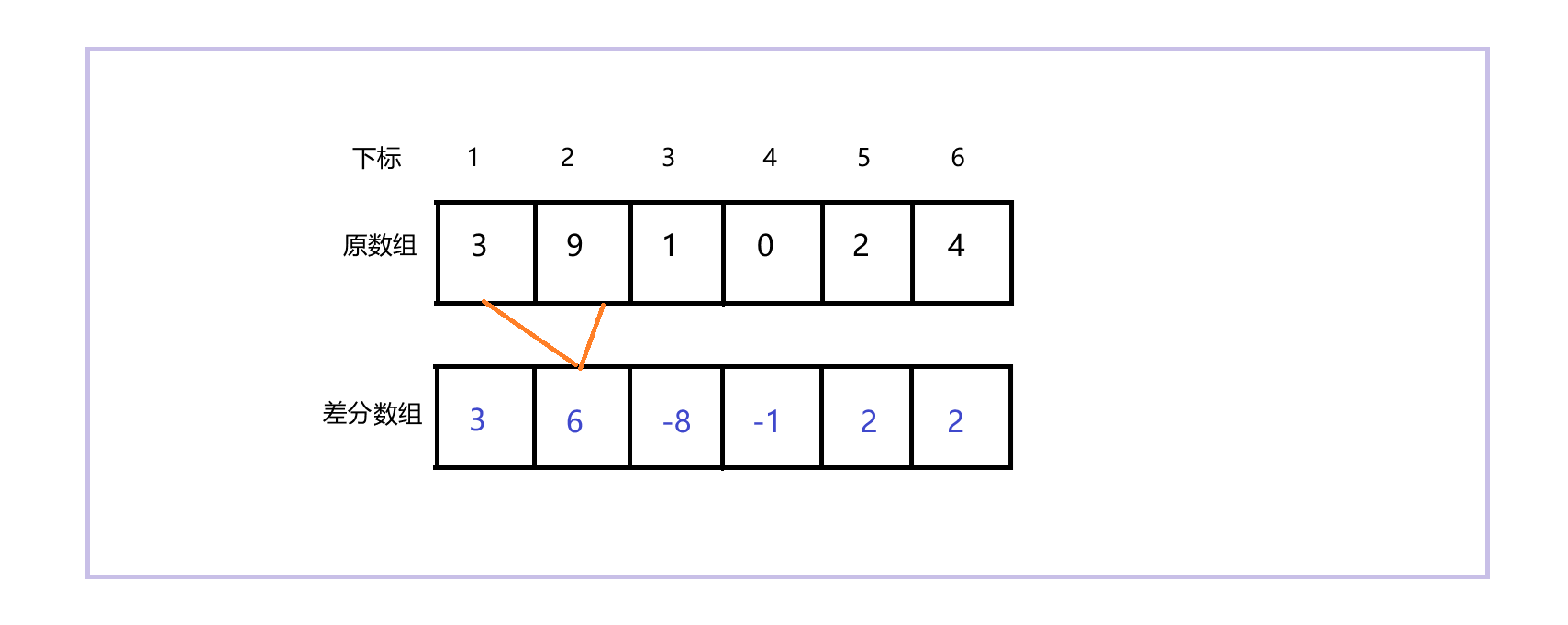
元素组为a，差分数组为f。

首先，给出f[i]的定义：f[ i ] = a[ i ] - a[ i - 1]。也就是当前位置对应的值与前一个位置的值的差。上图就是一个很朴素的差分数组，差分数组中每一个位置的值都是根据前面的公式计算出的。

其次，差分数组它有一个性质，就是a[ i ] = 差分数组中[1, i]区间内所有元素的和。比如a[ 4 ] = f[ 1 ] + f[ 2 ] + f[ 3 ] + f[ 4 ]。

那么，差分数组有什么用呢？换种说法，差分数组是用来解决什么问题的？这个问题我们先留着，来看看这样一个场景——给原数组中[2, 4]区间上的所有元素都加上一个2。很容易想到的一种解法是遍历该区间，然后给每个元素加上2。在引言部分我们已经说过了，这样会超时，所以引入了差分数组来解决。差分数组是如何解决的？它只需要修改两个位置的值即可，第一个位置是下标2，f[2] += 2，第二个位置是下标5，f[5] -= 2。只需这两步，就达到了给原数组中[2, 4]区间上的所有元素都加一个2的目标。

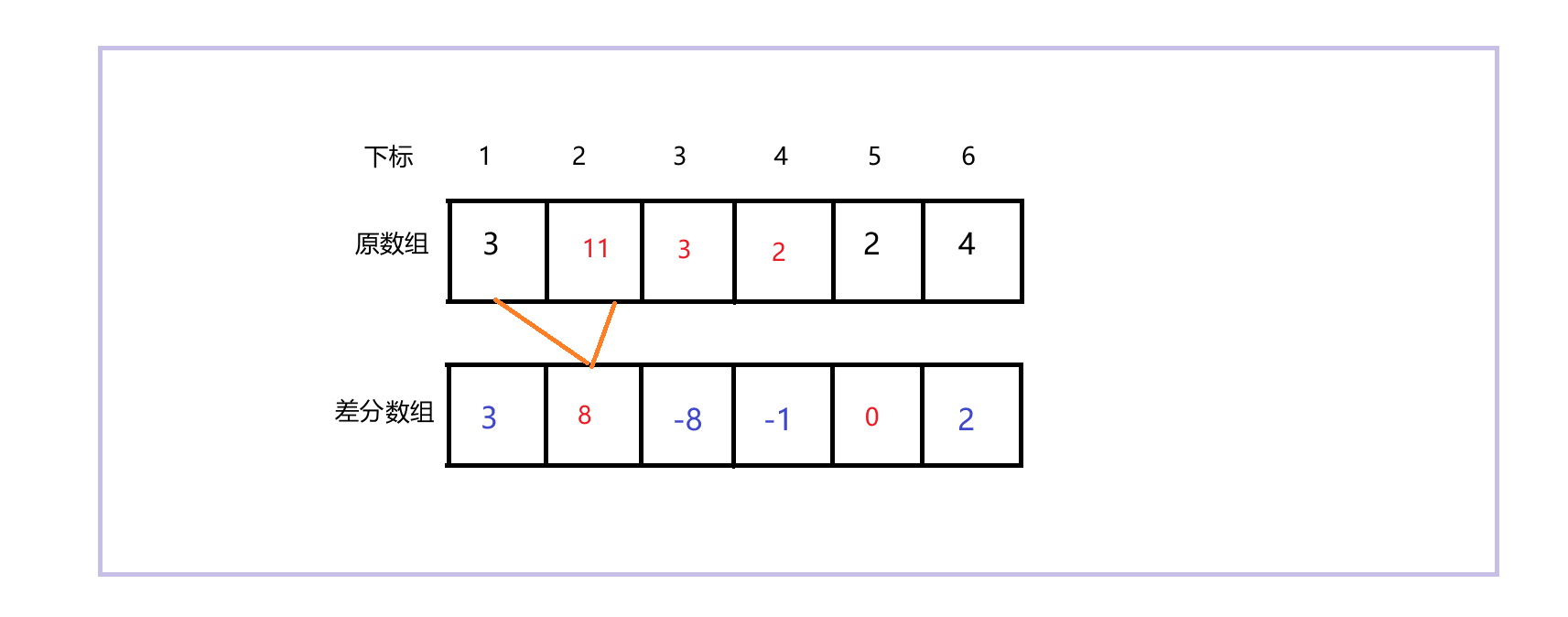
上图是给原数组中的[2, 4]区间上的所有元素都加上2之后的结果，差分数组也做了更新。通过差分数组的性质，我们可以验证一下通过差分数组是否可以正确推导出原数组。这里还请大家自行验证哈，我悄悄的验证过了，应该是没有问题的。这样，就证明了只需修改相应的两个位置的做法是对的。

上面的例子太特殊化，下面举一个更一般的例子，然后再得出结论。

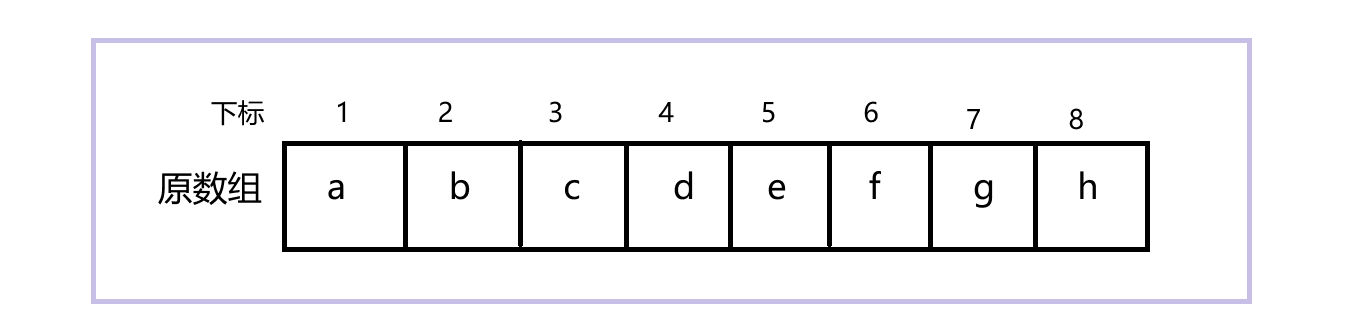
需求还是一样，对[2, 4]区间内的所有元素统一加一个k。此时，c - b的差值是不变的，d - c的差值也不变，原因很简单，因为大家都同时加上了同一个数。但由于a的值不变，它后边的b增加了k，那么b - a的差值必然也增加k，同理，e的值不变，d的值增加了k，那么e - d的差值必然要减少k，f和e、g和f……这些值都没有改变，自然它们的差也不变。

所以结论就是：对区间[L, R]内的所有元素统一加k，在差分数组中，只需执行这两个操作 f[L] += k，f[R + 1] -= k 。当然，k可以是正数，也可以是负数，无所谓，都统一执行这两个操作。下面，我们来一道模版题练练手，链接：一维差分模版题。代码：

#include <iostream>
using namespace std;

typedef long long LL;
const int N = 1e5 + 10;
LL f[N], a[N];//差分数组和原数组

int main()
{
    int n, m;
    cin >> n >> m;
    //根据定义来构造差分数组
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
        f[i] = a[i] - a[i - 1];
    }
    //第二种构造差分数组的方法
    /*
    for (int i = 1; i <= n; i++) {
        int val;
        cin >>val;
        f[i] += val;
        f[i + 1] -= val;
    }
    */
    while (m--) {
        int l, r, k;
        cin >> l >> r >> k;
        //套结论
        f[l] += k;
        f[r + 1] -= k;
    }
    //通过差分数组还原出原数组
    for (int i = 1; i <= n; i++) {
        f[i] = f[i - 1] + f[i];
        cout << f[i] << " ";
    }
    cout << endl;
    
    return 0;
}

除了通过定义去构造差分数组，还有一种更好的办法。

执行这两步：

1）f[ i ] += a[ i ]

2）f[ i + 1] -= a[ i ]

这实际上也是根据定义推出的。好处就是不用创建数组来存储原数据，节省一些空间。

二维差分

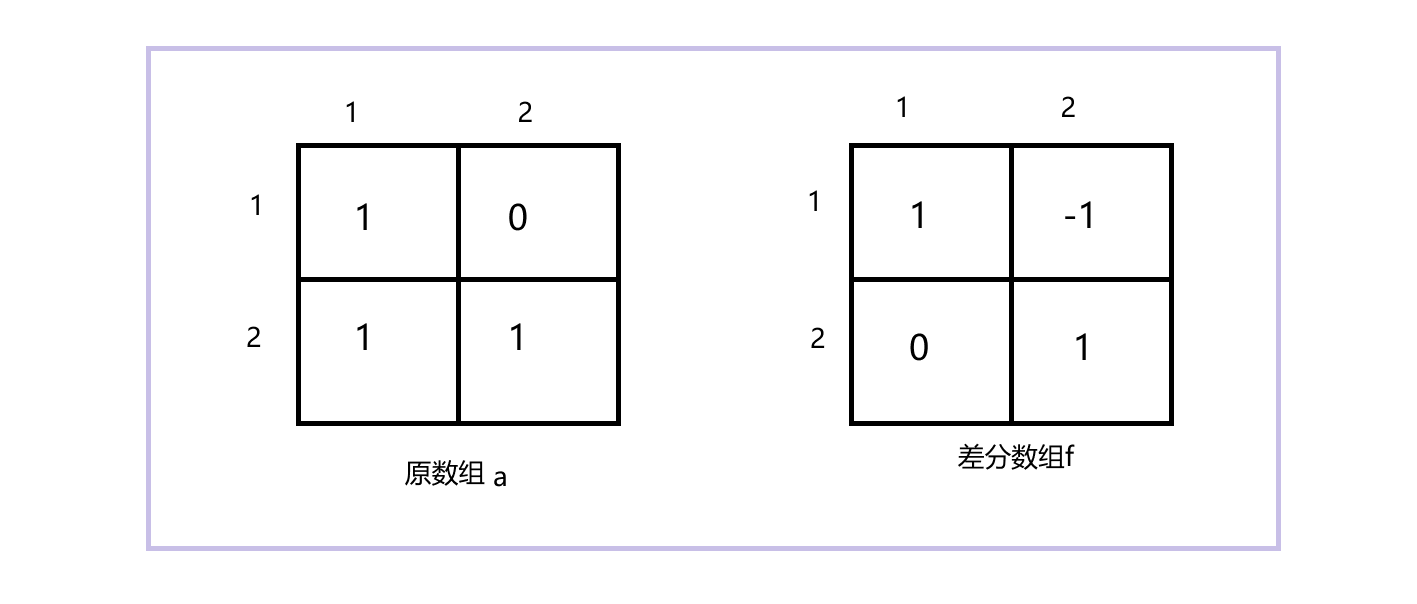
上图给出了原数组以及该数组所构建出来的差分数组。先不管是怎么构建出来的，我先分享一下我当时的困惑哈~

当时不知道f[ i ][ j ]表示什么意思，然后问了一下AI，给出的解释是：f[ i ][ j ]表示从（i, j）开始到矩阵右下角的区域的增量。是不是很抽象，没关系。要理解这句话，我们先要知道一点：在二维差分数组中，以（1,1）为左上角，以（i, j）为右下角构成的矩阵中所有元素的和就等于a[ i ][ j ]。到这里就不得不说如何构建二维差分数组了，一个式子：f[ i ][ j ] = a[ i ][ j ] - a[ i - 1 ][ j ] - a[ i ][ j - 1 ] + a[ i - 1][ j - 1]。我们可以通过这个公式去验证上面构造差分数组是否是正确的。

对了，这里需要再次声明，下标从1开始时为了避免越界，但凡下标中带0的，对应的值都是为0，也就是把差分数组开的大一些，剩余的部分0填充。

有了以上的知识储备，我们回到出发点——f[ i ][ j ]的含义，尤其是这个增量，到底是什么意思。

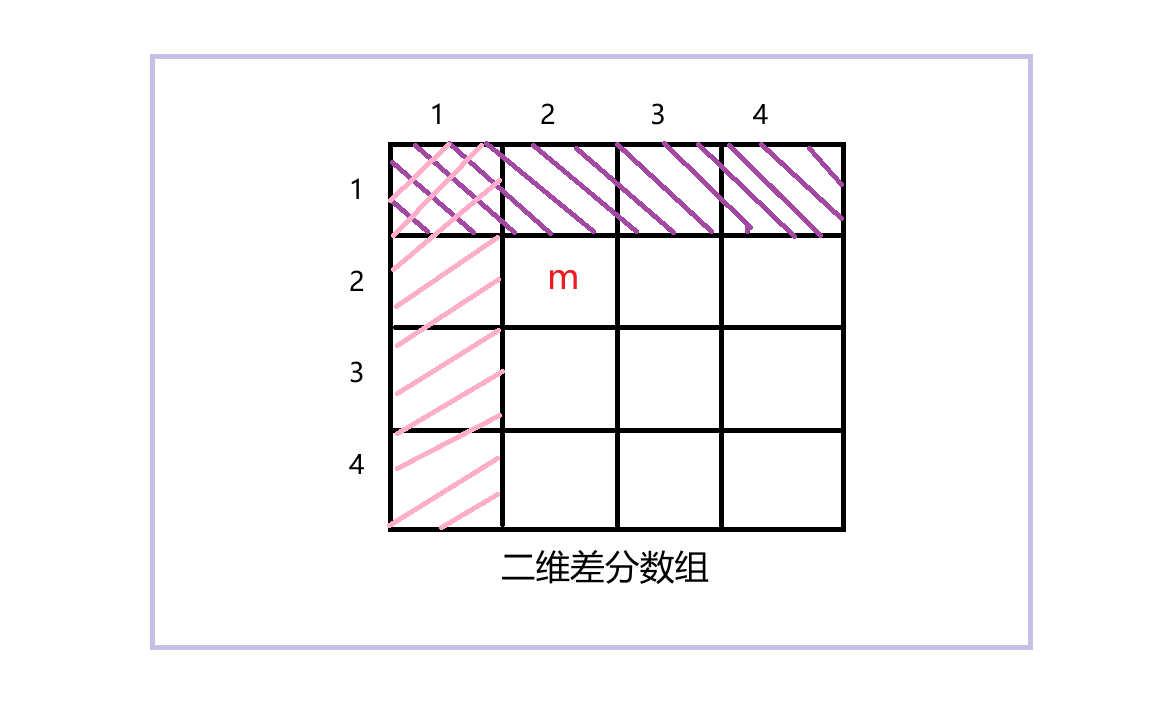
上图中，以（2,2）位置为例，f[2][2] = m。通过上面的学习，我们知道，在二维差分数组中，以（1,1）为左上角，以（i, j）为右下角构成的矩阵中所有元素的和就等于a[ i ][ j ]。我们在计算非阴影部分（没有斜线）对应的原数组中的值时，是需要加上m的，因为它在相应的矩阵内。但是，计算阴影部分对应的原数组中的值时，以（1,1）为左上角，以（i, j）为右下角构成的矩阵不包含（2,2）位置在里面，所以说，f[ i ][ j ]表示从（i, j）开始到矩阵右下角的区域的增量。比如我们在计算a[3][3]时，就需要加上m。

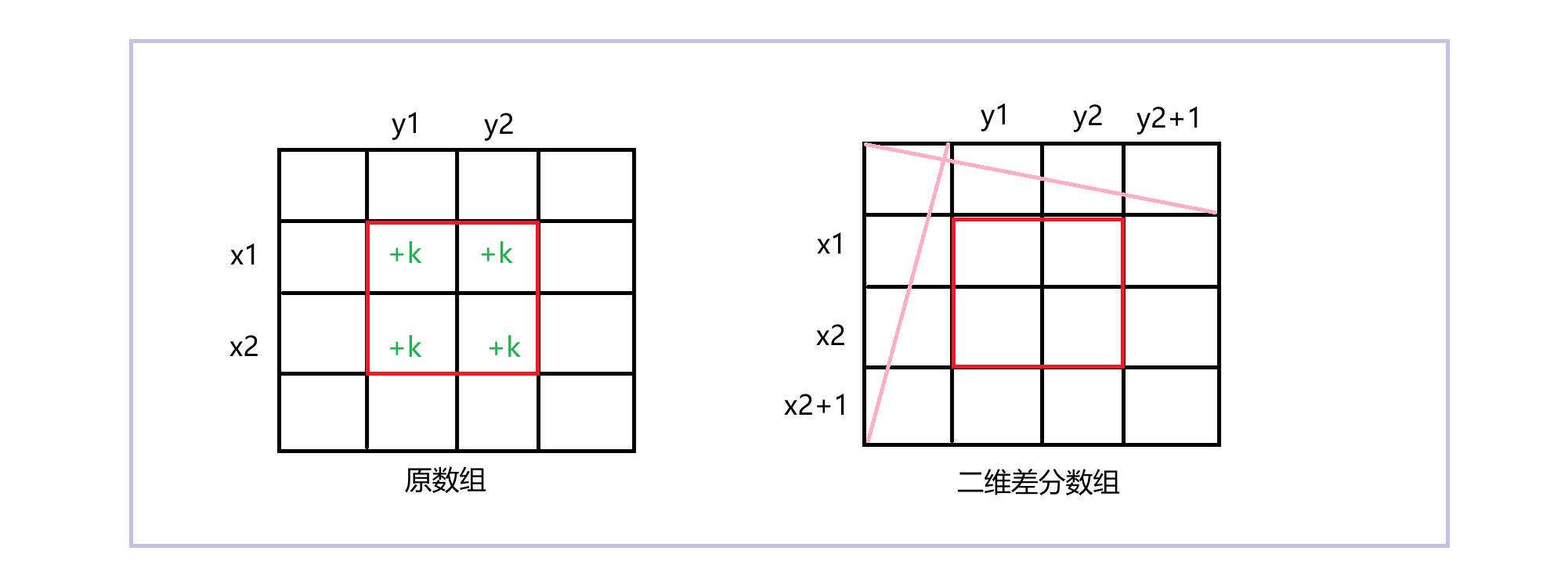
现在，有这样一个需求——在原数组中被框起来的位置所有元素都加上k。下面，我们来分析如何通过修改二维差分数组实现这一需求。

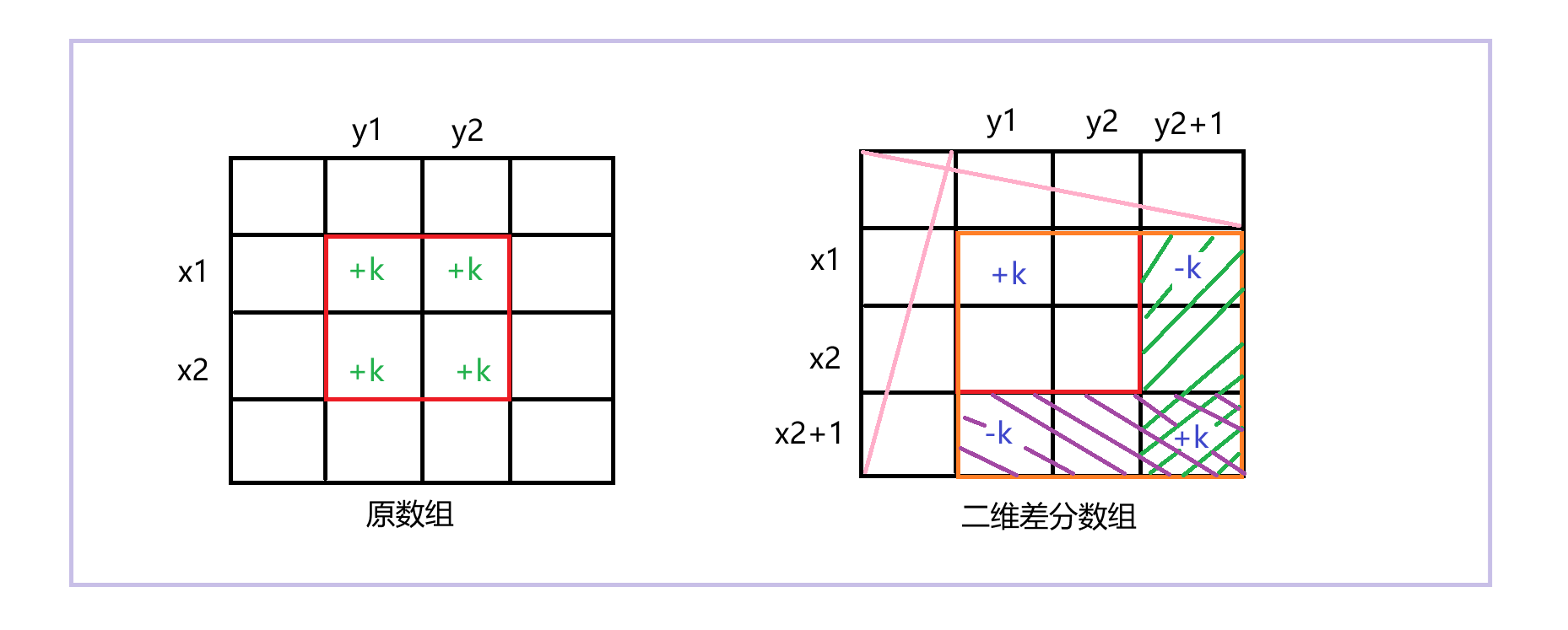
直接给出结论吧，然后在来分析为什么这么做。

f[x1][y1] += k

f[x1][y2+1] -= k

f[x2+1][y1] -= k

f[x2+1][y2+1] += k

以上四步就是核心，下面逐步分析。

f[x1][y1] += k，这样在计算a[x1][y1]时，以（1,1）为左上角，以（x1, y1）为右下角的矩阵中，所有元素的和增加了k，而我们知道，该矩阵中所有元素的和就是a[x1][y1]，就相当与a[x1][y1]在原来的基础上加了k。f[x1][y1] += k，会影响从（x1, y1）开始到矩阵右下角的区域，导致这些区域中的所有都增加了k，但这并不是我们想要的。

所以，f[x1][y2+1] -= k，f[x2+1][y1] -= k就分别抵消了绿色阴影部分和紫色阴影部分的影响，一个加k一个减k，自然就抵消了。

但是，也导致了绿色阴影和紫色阴影重叠的部分被减了两次，而只加了一次，需要再加上k抵消影响。这样，就将+k的影响限制在了红色框内，达到目的。

下面，介绍第二种构建二维差分数组的方法。

就是把构建差分数组看做是修改差分数组，每个矩阵都只有一个元素，进而利用以下结论（和上面的一样）：

f[x1][y1] += k

f[x1][y2+1] -= k

f[x2+1][y1] -= k

f[x2+1][y2+1] += k

这样做的好处是不需要原数组，进而节省了空间。下面我们来做一道算法题体会体会。题目链接：二维差分数组模版题。代码：

#include <iostream>
using namespace std;

typedef long long LL;
const int N = 1010;
LL f[N][N];

void insert(int x1, int y1, int x2, int y2, int k) {
    f[x1][y1] += k;
    f[x1][y2 + 1] -= k;
    f[x2 + 1][y1] -= k;
    f[x2 + 1][y2 + 1] += k;
}
int main()
{
    int n, m, q;
    cin >> n >> m >> q;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            int val;
            cin >> val;
            insert(i, j, i, j, val);
        }
    }
    while (q--) {
        int x1, y1, x2, y2, k;
        cin >> x1 >> y1 >> x2 >> y2 >> k;
        insert(x1, y1, x2, y2, k);
    }
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            //疑惑点，后面解释
            f[i][j] = f[i - 1][j] + f[i][j - 1] - f[i - 1][j - 1] + f[i][j];
            cout << f[i][j] << " ";
        } 
        cout << endl;
    }
    return 0;
}

解释代码中的疑惑点。

我当时一时没看懂这句代码是什么意思。根据公式 f[ i ][ j ] = a[ i ][ j ] - a[ i - 1 ][ j ] - a[ i ][ j - 1 ] + a[ i - 1][ j - 1]推a[ i ][ j ]，公式应该是a[ i ][ j ] = a[ i - 1 ][ j ] + a[ i ][ j - 1 ] - a[ i - 1][ j - 1] + f[ i ][ j ]呀！就是从这里开始，我开始迷了，不知道f[ i ][ j ]到底表示什么含义了。

实际计算原数组的公式是这个a[ i ][ j ] = a[ i - 1 ][ j ] + a[ i ][ j - 1 ] - a[ i - 1][ j - 1] + f[ i ][ j ]，但是为了节省空间不再开另一个数组来存储原数组，而是直接利用二维差分数组的空间来存放原数组中的值，所以覆盖掉二维差分数组，里面存的数据实际上就是原数组中的数据，也就是说上面公式中的f[][]存的值已经是a[][]，所以才可以写成这样 f[ i ][ j ] = f[ i - 1 ][ j ] + f[ i ][ j - 1 ] - f[ i - 1 ][ j - 1 ] + f[ i ][ j ]。f[ i - 1 ][ j ]中存放的值实际上就是原数组中a[ i - 1][ j ]的值，f[ i ][ j - 1 ]中存放的值实际上就是原数组中a[ i ][ j - 1 ]的值，f[ i ][ j ]中存放的值实际上就是原数组中a[ i ][ j ]的值。

明白了这一点之后，这段代码就不难理解了。