关于knn算法

最新推荐文章于 2025-03-03 22:37:48 发布

转载最新推荐文章于 2025-03-03 22:37:48 发布 · 212 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：https://blog.youkuaiyun.com/eeeee123456/article/details/79927128

python 专栏收录该内容

13 篇文章

订阅专栏

本文深入讲解了k-近邻（KNN）算法的基本原理和应用，包括算法的分类和回归功能，以及如何通过投票法和平均法进行预测。此外，还提供了KNN算法的Python实现代码，并介绍了kd树这一高效数据结构，用于加速k近邻搜索。

什么是knn，参考：https://zhuanlan.zhihu.com/p/61341071

knn参考代码：https://zhuanlan.zhihu.com/p/61996479 https://zhuanlan.zhihu.com/p/29925372 https://blog.youkuaiyun.com/lyq_12/article/details/81041007

算法原理

k-近邻（k-Nearest Neighbour，简称KNN），常用于有监督学习。

KNN的工作原理很简单：存在一个训练样本集合A，在给定测试样本b时，基于某种距离度量，找出训练集A中与测试样本b最靠近的k个训练样本（通常k≤20且为整数），之后，基于这k个训练样本的信息来预测种类或值。

其中，在分类问题中，KNN用来预测种类。一般使用“投票法”，选择这k个样本中出现最多的类别来作为测试样本的类别。

在回归问题中，KNN预测一个值。使用“平均法”，将k个样本的实值输出的平均值作为测试样本的输出。一般情况下，距离度量选择欧式距离：

伪代码如下：

对测试样本点进行以下操作：

(1)计算已知类别数据集中的点与当前点之间的距离；

(2)按照距离递增次序排序；

(3)选取与当前点距离最小的k个点；

(4)确定前k个点所在类别的出现频率；

(5)返回前k个点出现频率最高的类别作为当前点的预测分类。

代码：

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from pylab import *

#动态设置字体配置,避免无法正确显示字体
plt.rcParams['font.sans-serif'] = ['KaiTi']
plt.rcParams['font.serif'] = ['KaiTi']
# mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题,或者转换负号为字符串
sns.set_style("darkgrid",{"font.sans-serif":['KaiTi', 'Arial']})

##给出训练数据以及对应的类别
def createDataSet():
    group = np.array([[1.3,1.1],[3,2.7],[1.0,2.0],[1.2,0.1],[3,1.4],[3.4,3.5],[3.2,2.2],[3.5,2.7],[4,2.4]])
    labels = ['A','B','A','B','B','A','B','A','B']
    return group,labels

#计算欧氏距离
def get_distance(X,Y):
    return np.sum((X-Y)**2)**0.5

def knn(x_test,x_train,y_train,k):
    distances = []
    y_kind = {}
    #计算点到每个训练集样本的距离
    for i in x_train:
        distances.append(get_distance(x_test,i))
    tmp=list(enumerate(distances))#将distance列表组合为一个索引序列
    #根据索引列表的距离进行排序，取前k个距离最近的
    tmp.sort(key=lambda x:x[1])#针对元组构成的列表，使用key关键字
    min_k_dis=tmp[:k]

    #前k个的y标签进行字典统计
    for j in min_k_dis:
        t_key = y_train[j[0]] #标签 j[0]是索引下标
        #若y_kind含有此标签，则数量加一。否则添加该标签
        if t_key in y_kind.keys():
                y_kind[t_key] += 1
        else:
                y_kind.setdefault(t_key,1)
    #标签结果进行排序
    t=sorted(y_kind.items(),key=lambda x:x[1],reverse=True)
    #返回标签最多的一个
    return t[0][0] , min_k_dis[k-1]

#对测试数据使用knn算法判断其类型
group,label = createDataSet()#创建测试数据列表及其对应的标签
test = np.array([4,3.4])
n_neighbors = 5
output,farest = knn(test,group,label,n_neighbors)
print("测试数据为:",test,"分类结果为：",output)

kd树

实现k近邻法时，主要考虑的问题是如何对训练数据进行快速k近邻搜索，这点在特征空间的维数大及训练数据容量大时尤其必要。
k近邻法最简单的实现方法是线性扫描（linear scan），这时要计算输入实例与每一个训练实例的距离，当训练集很大时，计算非常耗时。为了提高k近邻法搜索的效率，可以考虑使用特殊的结构存储训练数据，以减少计算距离的次数。具体方法很多，下面介绍其中的kd树方法（kd树是存储k维空间数据的树结构，这里的k与k近邻法的k意义不同）。

例1 给定一个二维空间的数据集：D={(2,3)T,(5,4)T,(9,6)T,(4,7)T,(8,1)T,(7,2)T}D={(2,3)T,(5,4)T,(9,6)T,(4,7)T,(8,1)T,(7,2)T} D=\{(2,3)^T,(5,4)^T,(9,6)^T,(4,7)^T,(8,1)^T,(7,2)^T\}D={(2,3)T,(5,4)T,(9,6)T,(4,7)T,(8,1)T,(7,2)T}构造一个平衡kd树。
解：D为二维空间，则k=2。
① D中6个实例的x1坐标的中位数为7，则以(7 , 2)为切分点，由通过切分点并与坐标轴x1垂直的平面将超矩形区域切分为两个子区域。根结点为(7 , 2)，左区域包括：(2 , 3) , (5 , 4) , (4 , 7)，右区域包括：(8 , 1) , (9 , 6)，深度为1
② 对深度为j=1的结点，选择l=j(mod k)+1=1(mod 2)+1=2即x2为切分的坐标轴。则左区域的切分点为(5 , 4) ，左子区域为(2 , 3)，右子区域为(4 , 7)；右区域的切分点为(9 , 6) ，左子区域为(8 , 1)。

如此递归，最后得到的平衡kd树如下所示：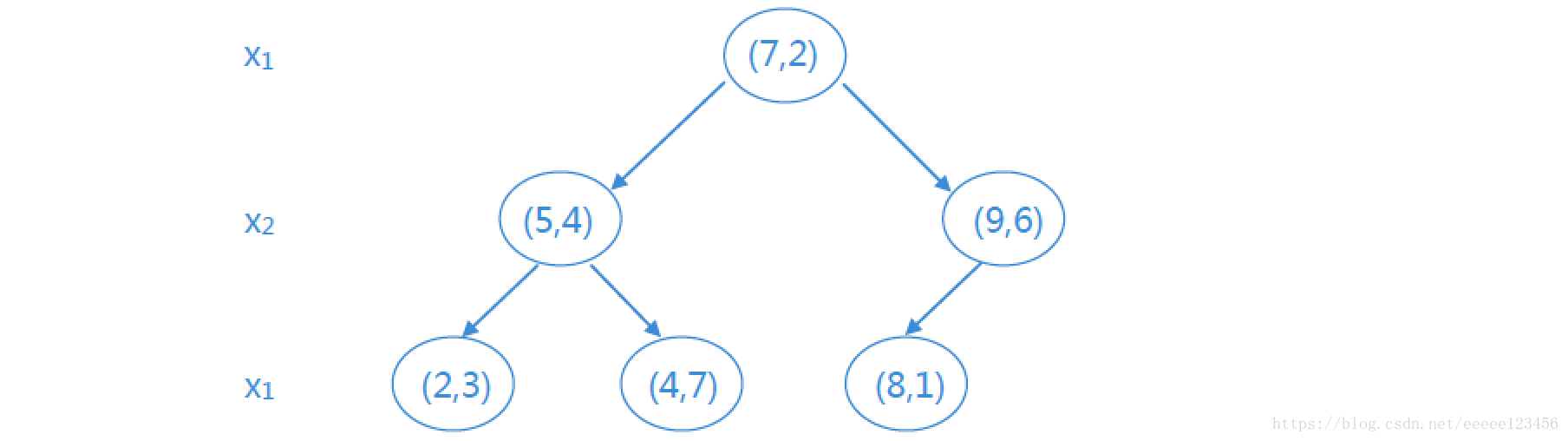
参考：https://blog.youkuaiyun.com/eeeee123456/article/details/79927128