不要使用容易被误解的名字

编码过程中要主动找到误解点，多问自己几遍该名字是否会被误解成别的意思。

比如filter这个词，大家可以理解成过滤，但是就比较不清楚，过滤是剔除还是保留呢？

1、推荐使用maxg与min来包含极限

编程时，经常为用到最大值最小值宏的定义，但是很多时候从字面我们无法理解，该值是否包含在范围内。比如说我们定义购物车中可以存放在最大物品数。

#define CARD_MAX_LIMITS  10

if(items >= CARD_MAX_LIMITS )

{

......

}

这种写法会造成大小差一的缺陷。CARD_MAX_LIMITS 的名字无法告诉我们是否包括10。但是这样定义将会消除二义性：

#define MAX_ITEMS_IN_CAR   10

if(items >= MAX_ITEMS_IN_CAR)

{

......

}

2、推荐使用first与last及begin与end表示范围

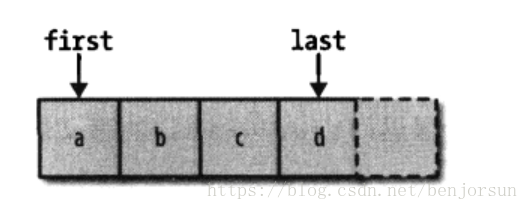
对于firt,last表示第一个与最后一个对象没有二义性，比start stop要好。但是对于表示“最后的下一个值”，英语没有更好的单词能代表，begin与end已经是最佳选择了。

以上例子只是说明，我们对变量起的名字要避免二义性。这样才能把程序当成注释。