Funky Numbers

最新推荐文章于 2025-12-30 06:51:55 发布

原创最新推荐文章于 2025-12-30 06:51:55 发布 · 407 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#c++ #算法

本文介绍了一种高效算法，用于判断一个给定的整数是否可以表示为两个三角形数之和。通过采用二分搜索策略，该算法能够在较短时间内找到解决方案。

As you very well know, this year's funkiest numbers are so called triangular numbers (that is, integers that are representable as , where k is some positive integer), and the coolest numbers are those that are representable as a sum of two triangular numbers.

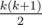
A well-known hipster Andrew adores everything funky and cool but unfortunately, he isn't good at maths. Given number n, help him define whether this number can be represented by a sum of two triangular numbers (not necessarily different)!

Input

The first input line contains an integer n (1 ≤ n ≤ 109).

Output

Print "YES" (without the quotes), if n can be represented as a sum of two triangular numbers, otherwise print "NO" (without the quotes).

Sample 1

Inputcopy	Outputcopy
256	YES

Sample 2

Inputcopy	Outputcopy
512	NO

Note

In the first sample number .

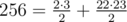
In the second sample number 512 can not be represented as a sum of two triangular numbers.

这个题目的话首先读题要读清楚，使用两组数字来表示，如果正常双重循环的话会超时，所以分开写，一个循环一个二分去写，然后数的话要注意，是sqrt（n * 2）因为n * ( n + 1) / 2，所以代码如下：

#include <iostream>
#include <cmath>

using namespace std;

const int N = 1e09;
typedef long long int ll;

int main() {
    ll n, l, r, flag = 0;

    cin >> n;
    ll h = sqrt(n * 2);
    for (int i = 1; i < h; i++) {
        ll l = i, r = h;
        while (l <= r) {
            ll mid = (l + r) / 2;
            if (mid * (mid + 1) / 2 + i * (i + 1) / 2 > n) r = mid - 1;
            else if (mid * (mid + 1) / 2 + i * (i + 1) / 2 < n) l = mid + 1;
            else {
                flag = 1;
                break;
            }
        } 
        if (flag) break;
    }
    if (flag) cout << "Yes" << endl;
    else cout << "No" << endl;
    return 0;
}

ok，润了