KNN

最新推荐文章于 2025-10-30 20:18:59 发布
原创 最新推荐文章于 2025-10-30 20:18:59 发布 · 2.8k 阅读 · 4 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

# K-近邻算法（KNN） K-nearest neighbor K-近邻算法 nearest 相近的 neighbor 邻居 ## 如何进行电影分类 众所周知，电影可以按照题材分类，然而题材本身是如何定义的?由谁来判定某部电影属于哪 个题材?也就是说同一题材的电影具有哪些公共特征?这些都是在进行电影分类时必须要考虑的问 题。没有哪个电影人会说自己制作的电影和以前的某部电影类似，但我们确实知道每部电影在风格 上的确有可能会和同题材的电影相近。那么动作片具有哪些共有特征，使得动作片之间非常类似， 而与爱情片存在着明显的差别呢？动作片中也会存在接吻镜头，爱情片中也会存在打斗场景，我们 不能单纯依靠是否存在打斗或者亲吻来判断影片的类型。但是爱情片中的亲吻镜头更多，动作片中 的打斗场景也更频繁，基于此类场景在某部电影中出现的次数可以用来进行电影分类。 本章介绍第一个机器学习算法：K-近邻算法，它非常有效而且易于掌握。 
import numpy as np
import pandas as pd
from pandas import Series, DataFrame
movie = pd.read_excel('./tests.xlsx', sheet_name=1)
movie
.dataframe tbody tr th:only-of-type { vertical-align: middle; } .dataframe tbody tr th { vertical-align: top; } .dataframe thead th { text-align: right; }
电影名称武打镜头接吻镜头分类情况
0大话西游361动作片
1杀破狼432动作片
2前任3010爱情片
3战狼2591动作片
4泰坦尼克号115爱情片
5星语心愿219爱情片
# 首先对于机器学习来说，字符串不代表可用数据，要么转成整数映射类型，要么不用
# X_train 表示的是要训练的数据
X_train = movie.iloc[:,1:-1]
# 答案
y_train = movie.iloc[:,-1:]
display(X_train, y_train)
.dataframe tbody tr th:only-of-type { vertical-align: middle; } .dataframe tbody tr th { vertical-align: top; } .dataframe thead th { text-align: right; }
武打镜头接吻镜头
0361
1432
2010
3591
4115
5219
.dataframe tbody tr th:only-of-type { vertical-align: middle; } .dataframe tbody tr th { vertical-align: top; } .dataframe thead th { text-align: right; }
分类情况
0动作片
1动作片
2爱情片
3动作片
4爱情片
5爱情片
# 引入机器学习的包
from sklearn.neighbors import KNeighborsClassifier
# n_neighbors默认值是5个，5个周围的样本
knn = KNeighborsClassifier(n_neighbors=5)
# 开始训练
knn.fit(X_train, y_train)

  • 输出

    KNeighborsClassifier(algorithm=’auto’, leaf_size=30, metric=’minkowski’,
    metric_params=None, n_jobs=1, n_neighbors=5, p=2,
    weights=’uniform’)

# 测试集
new_movie = DataFrame(np.array([['千星之城', 50, 10],['僵尸叔叔', 100, 2], ['超时空同居', 1, 12],['午夜凶铃', 0, 0]])
                     ,columns = ['电影名称', '武打镜头', '接吻镜头'])
new_movie
.dataframe tbody tr th:only-of-type { vertical-align: middle; } .dataframe tbody tr th { vertical-align: top; } .dataframe thead th { text-align: right; }
电影名称武打镜头接吻镜头
0千星之城5010
1僵尸叔叔1002
2超时空同居112
3午夜凶铃00
# 切片， 拿走没用的数据，比如电影名称
X_test = new_movie.iloc[:,1:]
X_test
.dataframe tbody tr th:only-of-type { vertical-align: middle; } .dataframe tbody tr th { vertical-align: top; } .dataframe thead th { text-align: right; }
武打镜头接吻镜头
05010
11002
2112
300
# 开始预测数据
y_test = knn.predict(X_test)
y_target = Series(y_test, name='分类情况')
y_target

  • 输出

    0 动作片
    1 动作片
    2 爱情片
    3 爱情片
    Name: 分类情况, dtype: object

data1 = pd.concat([new_movie, y_target], axis=1)
data1
.dataframe tbody tr th:only-of-type { vertical-align: middle; } .dataframe tbody tr th { vertical-align: top; } .dataframe thead th { text-align: right; }
电影名称武打镜头接吻镜头分类情况
0千星之城5010动作片
1僵尸叔叔1002动作片
2超时空同居112爱情片
3午夜凶铃00爱情片
data = pd.concat([movie, data1],ignore_index = True)
data
.dataframe tbody tr th:only-of-type { vertical-align: middle; } .dataframe tbody tr th { vertical-align: top; } .dataframe thead th { text-align: right; }
电影名称武打镜头接吻镜头分类情况
0大话西游361动作片
1杀破狼432动作片
2前任3010爱情片
3战狼2591动作片
4泰坦尼克号115爱情片
5星语心愿219爱情片
6千星之城5010动作片
7僵尸叔叔1002动作片
8超时空同居112爱情片
9午夜凶铃00爱情片
# 估测当前分类的准确值
y = Series(np.array(['动作片', '动作片', '爱情片', '动作片']), name='分类情况')
knn.score(X_test, y)

  • 输出

    0.75

1、k-近邻算法原理

简单地说，K-近邻算法采用测量不同特征值之间的距离方法进行分类。

  • 优点：精度高、对异常值不敏感、无数据输入假定。
  • 缺点：时间复杂度高、空间复杂度高。
  • 适用数据范围：数值型和标称型。

工作原理

存在一个样本数据集合，也称作训练样本集，并且样本集中每个数据都存在标签，即我们知道样本集中每一数据
与所属分类的对应关系。输人没有标签的新数据后，将新数据的每个特征与样本集中数据对应的
特征进行比较，然后算法提取样本集中特征最相似数据（最近邻）的分类标签。一般来说，我们
只选择样本数据集中前K个最相似的数据，这就是K-近邻算法中K的出处,通常*K是不大于20的整数。
最后 ，选择K个最相似数据中出现次数最多的分类，作为新数据的分类*。
回到前面电影分类的例子，使用K-近邻算法分类爱情片和动作片。有人曾经统计过很多电影的打斗镜头和接吻镜头，下图显示了6部电影的打斗和接吻次数。假如有一部未看过的电影，如何确定它是爱情片还是动作片呢？我们可以使用K-近邻算法来解决这个问题。
这里写图片描述

首先我们需要知道这个未知电影存在多少个打斗镜头和接吻镜头，上图中问号位置是该未知电影出现的镜头数图形化展示，具体数字参见下表。
这里写图片描述

即使不知道未知电影属于哪种类型，我们也可以通过某种方法计算出来。首先计算未知电影与样本集中其他电影的距离，如图所示。

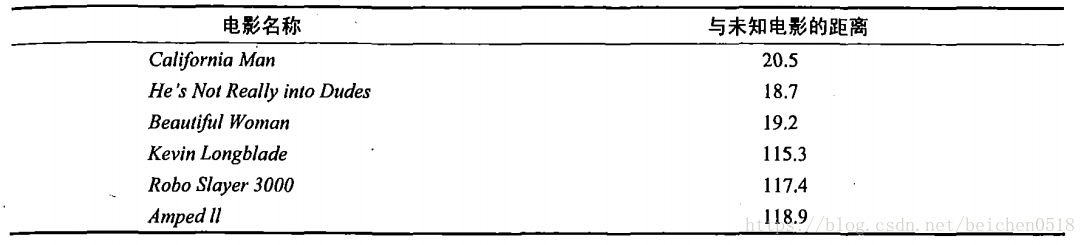
这里写图片描述
现在我们得到了样本集中所有电影与未知电影的距离，按照距离递增排序，可以找到K个距
离最近的电影。假定k=3，则三个最靠近的电影依次是California Man、He’s Not Really into Dudes、Beautiful Woman。K-近邻算法按照距离最近的三部电影的类型，决定未知电影的类型，而这三部电影全是爱情片，因此我们判定未知电影是爱情片。

欧几里得距离(Euclidean Distance)

欧氏距离是最常见的距离度量，衡量的是多维空间中各个点之间的绝对距离。公式如下：

这里写图片描述

2、在scikit-learn库中使用k-近邻算法

  • 分类问题：from sklearn.neighbors import KNeighborsClassifier

  • 回归问题：from sklearn.neighbors import KNeighborsRegressor

0）一个最简单的例子

我们根据身高、体重、鞋子尺码数据分析性别

# 给机器学习的数据必须是二维的
X_train = np.array([[180, 80, 44], [165, 45, 38], [162, 40, 36], [170, 82, 42], [170, 52, 40], [175, 67, 42]])
# 目标值是一维的数据
y_train = np.array(['男', '女', '女', '男','女', '男'])
#先机器学习
knn.fit(X_train, y_train)

  • 输出

    KNeighborsClassifier(algorithm=’auto’, leaf_size=30, metric=’minkowski’,
    metric_params=None, n_jobs=1, n_neighbors=5, p=2,
    weights=’uniform’)

# 定义预测的数据
X_test = np.array([[174, 72, 43], [163, 50, 38], [190, 80, 46]])
y = np.array(['男', '女', '女'])
# 开始预测
y_test = knn.predict(X_test)
y_test

  • 输出

    array([‘男’, ‘女’, ‘男’], dtype=’

knn.score(X_test, y)

  • 输出

    0.6666666666666666

把上面的数据转换成dataframe的

X_train_df = DataFrame(X_train, columns=['身高', '体重', '鞋码'])
y_train_df = DataFrame(y_train, columns=['性别'])

# 先学习
knn.fit(X_train_df, y_train_df)
KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
           metric_params=None, n_jobs=1, n_neighbors=5, p=2,
           weights='uniform')

knn.predict(X_test)

  • 输出

    array([‘男’, ‘女’, ‘男’], dtype=object)

鸢尾花识别

1）用于分类

导包，机器学习的算法KNN、数据蓝蝴蝶

import sklearn.datasets as datasets
iris = datasets.load_iris()
iris

  • 输出

    {‘DESCR’: ‘Iris Plants Database\n====================\n\nNotes\n—–\nData Set Characteristics:\n :Number of Instances: 150 (50 in each of three classes)\n :Number of Attributes: 4 numeric, predictive attributes and the class\n :Attribute Information:\n - sepal length in cm\n - sepal width in cm\n - petal length in cm\n - petal width in cm\n - class:\n - Iris-Setosa\n - Iris-Versicolour\n - Iris-Virginica\n :Summary Statistics:\n\n ============== ==== ==== ======= ===== ====================\n Min Max Mean SD Class Correlation\n ============== ==== ==== ======= ===== ====================\n sepal length: 4.3 7.9 5.84 0.83 0.7826\n sepal width: 2.0 4.4 3.05 0.43 -0.4194\n petal length: 1.0 6.9 3.76 1.76 0.9490 (high!)\n petal width: 0.1 2.5 1.20 0.76 0.9565 (high!)\n ============== ==== ==== ======= ===== ====================\n\n :Missing Attribute Values: None\n :Class Distribution: 33.3% for each of 3 classes.\n :Creator: R.A. Fisher\n :Donor: Michael Marshall (MARSHALL%PLU@io.arc.nasa.gov)\n :Date: July, 1988\n\nThis is a copy of UCI ML iris datasets.\nhttp://archive.ics.uci.edu/ml/datasets/Iris\n\nThe famous Iris database, first used by Sir R.A Fisher\n\nThis is perhaps the best known database to be found in the\npattern recognition literature. Fisher\’s paper is a classic in the field and\nis referenced frequently to this day. (See Duda & Hart, for example.) The\ndata set contains 3 classes of 50 instances each, where each class refers to a\ntype of iris plant. One class is linearly separable from the other 2; the\nlatter are NOT linearly separable from each other.\n\nReferences\n———-\n - Fisher,R.A. “The use of multiple measurements in taxonomic problems”\n Annual Eugenics, 7, Part II, 179-188 (1936); also in “Contributions to\n Mathematical Statistics” (John Wiley, NY, 1950).\n - Duda,R.O., & Hart,P.E. (1973) Pattern Classification and Scene Analysis.\n (Q327.D83) John Wiley & Sons. ISBN 0-471-22361-1. See page 218.\n - Dasarathy, B.V. (1980) “Nosing Around the Neighborhood: A New System\n Structure and Classification Rule for Recognition in Partially Exposed\n Environments”. IEEE Transactions on Pattern Analysis and Machine\n Intelligence, Vol. PAMI-2, No. 1, 67-71.\n - Gates, G.W. (1972) “The Reduced Nearest Neighbor Rule”. IEEE Transactions\n on Information Theory, May 1972, 431-433.\n - See also: 1988 MLC Proceedings, 54-64. Cheeseman et al”s AUTOCLASS II\n conceptual clustering system finds 3 classes in the data.\n - Many, many more …\n’,
    ‘data’: array([[5.1, 3.5, 1.4, 0.2],
    [4.9, 3. , 1.4, 0.2],
    [4.7, 3.2, 1.3, 0.2],
    [4.6, 3.1, 1.5, 0.2],
    [5. , 3.6, 1.4, 0.2],
    [5.4, 3.9, 1.7, 0.4],
    [4.6, 3.4, 1.4, 0.3],
    [5. , 3.4, 1.5, 0.2],
    [4.4, 2.9, 1.4, 0.2],
    [4.9, 3.1, 1.5, 0.1],
    [5.4, 3.7, 1.5, 0.2],
    [4.8, 3.4, 1.6, 0.2],
    [4.8, 3. , 1.4, 0.1],
    [4.3, 3. , 1.1, 0.1],
    [5.8, 4. , 1.2, 0.2],
    [5.7, 4.4, 1.5, 0.4],
    [5.4, 3.9, 1.3, 0.4],
    [5.1, 3.5, 1.4, 0.3],
    [5.7, 3.8, 1.7, 0.3],
    [5.1, 3.8, 1.5, 0.3],
    [5.4, 3.4, 1.7, 0.2],
    [5.1, 3.7, 1.5, 0.4],
    [4.6, 3.6, 1. , 0.2],
    [5.1, 3.3, 1.7, 0.5],
    [4.8, 3.4, 1.9, 0.2],
    [5. , 3. , 1.6, 0.2],
    [5. , 3.4, 1.6, 0.4],
    [5.2, 3.5, 1.5, 0.2],
    [5.2, 3.4, 1.4, 0.2],
    [4.7, 3.2, 1.6, 0.2],
    [4.8, 3.1, 1.6, 0.2],
    [5.4, 3.4, 1.5, 0.4],
    [5.2, 4.1, 1.5, 0.1],
    [5.5, 4.2, 1.4, 0.2],
    [4.9, 3.1, 1.5, 0.1],
    [5. , 3.2, 1.2, 0.2],
    [5.5, 3.5, 1.3, 0.2],
    [4.9, 3.1, 1.5, 0.1],
    [4.4, 3. , 1.3, 0.2],
    [5.1, 3.4, 1.5, 0.2],
    [5. , 3.5, 1.3, 0.3],
    [4.5, 2.3, 1.3, 0.3],
    [4.4, 3.2, 1.3, 0.2],
    [5. , 3.5, 1.6, 0.6],
    [5.1, 3.8, 1.9, 0.4],
    [4.8, 3. , 1.4, 0.3],
    [5.1, 3.8, 1.6, 0.2],
    [4.6, 3.2, 1.4, 0.2],
    [5.3, 3.7, 1.5, 0.2],
    [5. , 3.3, 1.4, 0.2],
    [7. , 3.2, 4.7, 1.4],
    [6.4, 3.2, 4.5, 1.5],
    [6.9, 3.1, 4.9, 1.5],
    [5.5, 2.3, 4. , 1.3],
    [6.5, 2.8, 4.6, 1.5],
    [5.7, 2.8, 4.5, 1.3],
    [6.3, 3.3, 4.7, 1.6],
    [4.9, 2.4, 3.3, 1. ],
    [6.6, 2.9, 4.6, 1.3],
    [5.2, 2.7, 3.9, 1.4],
    [5. , 2. , 3.5, 1. ],
    [5.9, 3. , 4.2, 1.5],
    [6. , 2.2, 4. , 1. ],
    [6.1, 2.9, 4.7, 1.4],
    [5.6, 2.9, 3.6, 1.3],
    [6.7, 3.1, 4.4, 1.4],
    [5.6, 3. , 4.5, 1.5],
    [5.8, 2.7, 4.1, 1. ],
    [6.2, 2.2, 4.5, 1.5],
    [5.6, 2.5, 3.9, 1.1],
    [5.9, 3.2, 4.8, 1.8],
    [6.1, 2.8, 4. , 1.3],
    [6.3, 2.5, 4.9, 1.5],
    [6.1, 2.8, 4.7, 1.2],
    [6.4, 2.9, 4.3, 1.3],
    [6.6, 3. , 4.4, 1.4],
    [6.8, 2.8, 4.8, 1.4],
    [6.7, 3. , 5. , 1.7],
    [6. , 2.9, 4.5, 1.5],
    [5.7, 2.6, 3.5, 1. ],
    [5.5, 2.4, 3.8, 1.1],
    [5.5, 2.4, 3.7, 1. ],
    [5.8, 2.7, 3.9, 1.2],
    [6. , 2.7, 5.1, 1.6],
    [5.4, 3. , 4.5, 1.5],
    [6. , 3.4, 4.5, 1.6],
    [6.7, 3.1, 4.7, 1.5],
    [6.3, 2.3, 4.4, 1.3],
    [5.6, 3. , 4.1, 1.3],
    [5.5, 2.5, 4. , 1.3],
    [5.5, 2.6, 4.4, 1.2],
    [6.1, 3. , 4.6, 1.4],
    [5.8, 2.6, 4. , 1.2],
    [5. , 2.3, 3.3, 1. ],
    [5.6, 2.7, 4.2, 1.3],
    [5.7, 3. , 4.2, 1.2],
    [5.7, 2.9, 4.2, 1.3],
    [6.2, 2.9, 4.3, 1.3],
    [5.1, 2.5, 3. , 1.1],
    [5.7, 2.8, 4.1, 1.3],
    [6.3, 3.3, 6. , 2.5],
    [5.8, 2.7, 5.1, 1.9],
    [7.1, 3. , 5.9, 2.1],
    [6.3, 2.9, 5.6, 1.8],
    [6.5, 3. , 5.8, 2.2],
    [7.6, 3. , 6.6, 2.1],
    [4.9, 2.5, 4.5, 1.7],
    [7.3, 2.9, 6.3, 1.8],
    [6.7, 2.5, 5.8, 1.8],
    [7.2, 3.6, 6.1, 2.5],
    [6.5, 3.2, 5.1, 2. ],
    [6.4, 2.7, 5.3, 1.9],
    [6.8, 3. , 5.5, 2.1],
    [5.7, 2.5, 5. , 2. ],
    [5.8, 2.8, 5.1, 2.4],
    [6.4, 3.2, 5.3, 2.3],
    [6.5, 3. , 5.5, 1.8],
    [7.7, 3.8, 6.7, 2.2],
    [7.7, 2.6, 6.9, 2.3],
    [6. , 2.2, 5. , 1.5],
    [6.9, 3.2, 5.7, 2.3],
    [5.6, 2.8, 4.9, 2. ],
    [7.7, 2.8, 6.7, 2. ],
    [6.3, 2.7, 4.9, 1.8],
    [6.7, 3.3, 5.7, 2.1],
    [7.2, 3.2, 6. , 1.8],
    [6.2, 2.8, 4.8, 1.8],
    [6.1, 3. , 4.9, 1.8],
    [6.4, 2.8, 5.6, 2.1],
    [7.2, 3. , 5.8, 1.6],
    [7.4, 2.8, 6.1, 1.9],
    [7.9, 3.8, 6.4, 2. ],
    [6.4, 2.8, 5.6, 2.2],
    [6.3, 2.8, 5.1, 1.5],
    [6.1, 2.6, 5.6, 1.4],
    [7.7, 3. , 6.1, 2.3],
    [6.3, 3.4, 5.6, 2.4],
    [6.4, 3.1, 5.5, 1.8],
    [6. , 3. , 4.8, 1.8],
    [6.9, 3.1, 5.4, 2.1],
    [6.7, 3.1, 5.6, 2.4],
    [6.9, 3.1, 5.1, 2.3],
    [5.8, 2.7, 5.1, 1.9],
    [6.8, 3.2, 5.9, 2.3],
    [6.7, 3.3, 5.7, 2.5],
    [6.7, 3. , 5.2, 2.3],
    [6.3, 2.5, 5. , 1.9],
    [6.5, 3. , 5.2, 2. ],
    [6.2, 3.4, 5.4, 2.3],
    [5.9, 3. , 5.1, 1.8]]),
    ‘feature_names’: [‘sepal length (cm)’,
    ‘sepal width (cm)’,
    ‘petal length (cm)’,
    ‘petal width (cm)’],
    ‘target’: array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
    0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
    0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
    1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
    1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
    2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
    2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2]),
    ‘target_names’: array([‘setosa’, ‘versicolor’, ‘virginica’], dtype=’

data = iris['data']
data

  • 输出

    array([[5.1, 3.5, 1.4, 0.2],
    [4.9, 3. , 1.4, 0.2],
    [4.7, 3.2, 1.3, 0.2],
    [4.6, 3.1, 1.5, 0.2],
    [5. , 3.6, 1.4, 0.2],
    [5.4, 3.9, 1.7, 0.4],
    [4.6, 3.4, 1.4, 0.3],
    [5. , 3.4, 1.5, 0.2],
    [4.4, 2.9, 1.4, 0.2],
    [4.9, 3.1, 1.5, 0.1],
    [5.4, 3.7, 1.5, 0.2],
    [4.8, 3.4, 1.6, 0.2],
    [4.8, 3. , 1.4, 0.1],
    [4.3, 3. , 1.1, 0.1],
    [5.8, 4. , 1.2, 0.2],
    [5.7, 4.4, 1.5, 0.4],
    [5.4, 3.9, 1.3, 0.4],
    [5.1, 3.5, 1.4, 0.3],
    [5.7, 3.8, 1.7, 0.3],
    [5.1, 3.8, 1.5, 0.3],
    [5.4, 3.4, 1.7, 0.2],
    [5.1, 3.7, 1.5, 0.4],
    [4.6, 3.6, 1. , 0.2],
    [5.1, 3.3, 1.7, 0.5],
    [4.8, 3.4, 1.9, 0.2],
    [5. , 3. , 1.6, 0.2],
    [5. , 3.4, 1.6, 0.4],
    [5.2, 3.5, 1.5, 0.2],
    [5.2, 3.4, 1.4, 0.2],
    [4.7, 3.2, 1.6, 0.2],
    [4.8, 3.1, 1.6, 0.2],
    [5.4, 3.4, 1.5, 0.4],
    [5.2, 4.1, 1.5, 0.1],
    [5.5, 4.2, 1.4, 0.2],
    [4.9, 3.1, 1.5, 0.1],
    [5. , 3.2, 1.2, 0.2],
    [5.5, 3.5, 1.3, 0.2],
    [4.9, 3.1, 1.5, 0.1],
    [4.4, 3. , 1.3, 0.2],
    [5.1, 3.4, 1.5, 0.2],
    [5. , 3.5, 1.3, 0.3],
    [4.5, 2.3, 1.3, 0.3],
    [4.4, 3.2, 1.3, 0.2],
    [5. , 3.5, 1.6, 0.6],
    [5.1, 3.8, 1.9, 0.4],
    [4.8, 3. , 1.4, 0.3],
    [5.1, 3.8, 1.6, 0.2],
    [4.6, 3.2, 1.4, 0.2],
    [5.3, 3.7, 1.5, 0.2],
    [5. , 3.3, 1.4, 0.2],
    [7. , 3.2, 4.7, 1.4],
    [6.4, 3.2, 4.5, 1.5],
    [6.9, 3.1, 4.9, 1.5],
    [5.5, 2.3, 4. , 1.3],
    [6.5, 2.8, 4.6, 1.5],
    [5.7, 2.8, 4.5, 1.3],
    [6.3, 3.3, 4.7, 1.6],
    [4.9, 2.4, 3.3, 1. ],
    [6.6, 2.9, 4.6, 1.3],
    [5.2, 2.7, 3.9, 1.4],
    [5. , 2. , 3.5, 1. ],
    [5.9, 3. , 4.2, 1.5],
    [6. , 2.2, 4. , 1. ],
    [6.1, 2.9, 4.7, 1.4],
    [5.6, 2.9, 3.6, 1.3],
    [6.7, 3.1, 4.4, 1.4],
    [5.6, 3. , 4.5, 1.5],
    [5.8, 2.7, 4.1, 1. ],
    [6.2, 2.2, 4.5, 1.5],
    [5.6, 2.5, 3.9, 1.1],
    [5.9, 3.2, 4.8, 1.8],
    [6.1, 2.8, 4. , 1.3],
    [6.3, 2.5, 4.9, 1.5],
    [6.1, 2.8, 4.7, 1.2],
    [6.4, 2.9, 4.3, 1.3],
    [6.6, 3. , 4.4, 1.4],
    [6.8, 2.8, 4.8, 1.4],
    [6.7, 3. , 5. , 1.7],
    [6. , 2.9, 4.5, 1.5],
    [5.7, 2.6, 3.5, 1. ],
    [5.5, 2.4, 3.8, 1.1],
    [5.5, 2.4, 3.7, 1. ],
    [5.8, 2.7, 3.9, 1.2],
    [6. , 2.7, 5.1, 1.6],
    [5.4, 3. , 4.5, 1.5],
    [6. , 3.4, 4.5, 1.6],
    [6.7, 3.1, 4.7, 1.5],
    [6.3, 2.3, 4.4, 1.3],
    [5.6, 3. , 4.1, 1.3],
    [5.5, 2.5, 4. , 1.3],
    [5.5, 2.6, 4.4, 1.2],
    [6.1, 3. , 4.6, 1.4],
    [5.8, 2.6, 4. , 1.2],
    [5. , 2.3, 3.3, 1. ],
    [5.6, 2.7, 4.2, 1.3],
    [5.7, 3. , 4.2, 1.2],
    [5.7, 2.9, 4.2, 1.3],
    [6.2, 2.9, 4.3, 1.3],
    [5.1, 2.5, 3. , 1.1],
    [5.7, 2.8, 4.1, 1.3],
    [6.3, 3.3, 6. , 2.5],
    [5.8, 2.7, 5.1, 1.9],
    [7.1, 3. , 5.9, 2.1],
    [6.3, 2.9, 5.6, 1.8],
    [6.5, 3. , 5.8, 2.2],
    [7.6, 3. , 6.6, 2.1],
    [4.9, 2.5, 4.5, 1.7],
    [7.3, 2.9, 6.3, 1.8],
    [6.7, 2.5, 5.8, 1.8],
    [7.2, 3.6, 6.1, 2.5],
    [6.5, 3.2, 5.1, 2. ],
    [6.4, 2.7, 5.3, 1.9],
    [6.8, 3. , 5.5, 2.1],
    [5.7, 2.5, 5. , 2. ],
    [5.8, 2.8, 5.1, 2.4],
    [6.4, 3.2, 5.3, 2.3],
    [6.5, 3. , 5.5, 1.8],
    [7.7, 3.8, 6.7, 2.2],
    [7.7, 2.6, 6.9, 2.3],
    [6. , 2.2, 5. , 1.5],
    [6.9, 3.2, 5.7, 2.3],
    [5.6, 2.8, 4.9, 2. ],
    [7.7, 2.8, 6.7, 2. ],
    [6.3, 2.7, 4.9, 1.8],
    [6.7, 3.3, 5.7, 2.1],
    [7.2, 3.2, 6. , 1.8],
    [6.2, 2.8, 4.8, 1.8],
    [6.1, 3. , 4.9, 1.8],
    [6.4, 2.8, 5.6, 2.1],
    [7.2, 3. , 5.8, 1.6],
    [7.4, 2.8, 6.1, 1.9],
    [7.9, 3.8, 6.4, 2. ],
    [6.4, 2.8, 5.6, 2.2],
    [6.3, 2.8, 5.1, 1.5],
    [6.1, 2.6, 5.6, 1.4],
    [7.7, 3. , 6.1, 2.3],
    [6.3, 3.4, 5.6, 2.4],
    [6.4, 3.1, 5.5, 1.8],
    [6. , 3. , 4.8, 1.8],
    [6.9, 3.1, 5.4, 2.1],
    [6.7, 3.1, 5.6, 2.4],
    [6.9, 3.1, 5.1, 2.3],
    [5.8, 2.7, 5.1, 1.9],
    [6.8, 3.2, 5.9, 2.3],
    [6.7, 3.3, 5.7, 2.5],
    [6.7, 3. , 5.2, 2.3],
    [6.3, 2.5, 5. , 1.9],
    [6.5, 3. , 5.2, 2. ],
    [6.2, 3.4, 5.4, 2.3],
    [5.9, 3. , 5.1, 1.8]])

target = iris['target']
target

  • 输出

    array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
    0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
    0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
    1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
    1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
    2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
    2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])

target_names = iris['target_names']
target_names

  • 输出

    array([‘setosa’, ‘versicolor’, ‘virginica’], dtype=’

target_names[target[0]]

  • 输出

    ‘setosa’

data.shape

  • 输出

    (150, 4)

获取训练样本

# 因为我们没有鸢尾花专家，那我们的预测数据就会受到限制，？
# 一共150个样本，我们可以抽取一部分，这一部分就不能机器学习
# 它的作用是将测试数据和预测数据分开的
from sklearn.model_selection import train_test_split
nd = np.arange(0, 20)
nd1 = np.arange(30, 50)
train_test_split(nd, nd1, test_size=0.1)

  • 输出

    [array([ 4, 6, 3, 16, 19, 17, 13, 12, 2, 5, 18, 10, 7, 15, 1, 8, 11,
    9]),
    array([ 0, 14]),
    array([34, 36, 33, 46, 49, 47, 43, 42, 32, 35, 48, 40, 37, 45, 31, 38, 41,
    39]),
    array([30, 44])]

# 150, 15预测， 135学习
# 将数据分割
X_train, X_test, y_train, y_test = train_test_split(data, target, test_size=0.1)
display(X_train, X_test, y_train, y_test)

  • 输出

    array([[4.8, 3.4, 1.6, 0.2],
    [6.4, 3.2, 4.5, 1.5],
    [6.1, 2.6, 5.6, 1.4],
    [5.7, 3.8, 1.7, 0.3],
    [5.8, 4. , 1.2, 0.2],
    [5.5, 2.4, 3.7, 1. ],
    [5.1, 3.7, 1.5, 0.4],
    [6.3, 2.7, 4.9, 1.8],
    [6.7, 3.1, 5.6, 2.4],
    [5.8, 2.7, 5.1, 1.9],
    [7.2, 3. , 5.8, 1.6],
    [4.9, 3. , 1.4, 0.2],
    [5.6, 2.9, 3.6, 1.3],
    [6.1, 3. , 4.6, 1.4],
    [4.4, 2.9, 1.4, 0.2],
    [6. , 3. , 4.8, 1.8],
    [5.5, 2.5, 4. , 1.3],
    [6.9, 3.1, 5.4, 2.1],
    [5.1, 2.5, 3. , 1.1],
    [6.4, 2.9, 4.3, 1.3],
    [5.6, 3. , 4.1, 1.3],
    [5. , 2. , 3.5, 1. ],
    [7.7, 3. , 6.1, 2.3],
    [6.7, 3.1, 4.4, 1.4],
    [4.8, 3.1, 1.6, 0.2],
    [5.6, 2.8, 4.9, 2. ],
    [5.4, 3.4, 1.7, 0.2],
    [6. , 3.4, 4.5, 1.6],
    [6.7, 3.1, 4.7, 1.5],
    [5.7, 2.9, 4.2, 1.3],
    [6.3, 3.3, 6. , 2.5],
    [6.1, 2.8, 4. , 1.3],
    [5.7, 2.6, 3.5, 1. ],
    [4.9, 3.1, 1.5, 0.1],
    [5.2, 2.7, 3.9, 1.4],
    [7.7, 3.8, 6.7, 2.2],
    [5.6, 2.7, 4.2, 1.3],
    [5.8, 2.6, 4. , 1.2],
    [5.1, 3.5, 1.4, 0.3],
    [6.2, 2.9, 4.3, 1.3],
    [6.4, 2.8, 5.6, 2.2],
    [6.8, 2.8, 4.8, 1.4],
    [7.7, 2.8, 6.7, 2. ],
    [6.4, 3.2, 5.3, 2.3],
    [7.4, 2.8, 6.1, 1.9],
    [6. , 2.2, 4. , 1. ],
    [5.8, 2.8, 5.1, 2.4],
    [5.7, 2.5, 5. , 2. ],
    [5.5, 4.2, 1.4, 0.2],
    [5. , 3.4, 1.6, 0.4],
    [7.6, 3. , 6.6, 2.1],
    [6.2, 2.2, 4.5, 1.5],
    [4.4, 3. , 1.3, 0.2],
    [5.9, 3. , 5.1, 1.8],
    [4.6, 3.1, 1.5, 0.2],
    [5.6, 3. , 4.5, 1.5],
    [6.5, 3. , 5.8, 2.2],
    [6.5, 3. , 5.2, 2. ],
    [6.5, 2.8, 4.6, 1.5],
    [5.2, 4.1, 1.5, 0.1],
    [6.7, 3.3, 5.7, 2.5],
    [4.6, 3.6, 1. , 0.2],
    [6.2, 2.8, 4.8, 1.8],
    [5. , 3.2, 1.2, 0.2],
    [5.5, 2.3, 4. , 1.3],
    [7.3, 2.9, 6.3, 1.8],
    [4.7, 3.2, 1.3, 0.2],
    [5.1, 3.3, 1.7, 0.5],
    [6.1, 2.9, 4.7, 1.4],
    [5.1, 3.4, 1.5, 0.2],
    [6.7, 3. , 5.2, 2.3],
    [6.3, 2.8, 5.1, 1.5],
    [5.5, 3.5, 1.3, 0.2],
    [7.2, 3.2, 6. , 1.8],
    [4.5, 2.3, 1.3, 0.3],
    [6.3, 2.9, 5.6, 1.8],
    [6.3, 3.4, 5.6, 2.4],
    [7.7, 2.6, 6.9, 2.3],
    [5.6, 2.5, 3.9, 1.1],
    [5.8, 2.7, 4.1, 1. ],
    [5.2, 3.4, 1.4, 0.2],
    [5.8, 2.7, 5.1, 1.9],
    [4.6, 3.4, 1.4, 0.3],
    [4.9, 2.5, 4.5, 1.7],
    [5.4, 3.9, 1.7, 0.4],
    [7.2, 3.6, 6.1, 2.5],
    [5.9, 3. , 4.2, 1.5],
    [6.3, 3.3, 4.7, 1.6],
    [6. , 2.7, 5.1, 1.6],
    [4.7, 3.2, 1.6, 0.2],
    [5.1, 3.8, 1.5, 0.3],
    [5. , 3.4, 1.5, 0.2],
    [4.8, 3.4, 1.9, 0.2],
    [5.1, 3.8, 1.6, 0.2],
    [5.9, 3.2, 4.8, 1.8],
    [5.1, 3.5, 1.4, 0.2],
    [6.9, 3.1, 5.1, 2.3],
    [6.5, 3. , 5.5, 1.8],
    [5.5, 2.6, 4.4, 1.2],
    [5.4, 3.7, 1.5, 0.2],
    [5.1, 3.8, 1.9, 0.4],
    [5. , 3.5, 1.6, 0.6],
    [6.4, 2.7, 5.3, 1.9],
    [5.4, 3.9, 1.3, 0.4],
    [5. , 2.3, 3.3, 1. ],
    [4.3, 3. , 1.1, 0.1],
    [5.5, 2.4, 3.8, 1.1],
    [6.6, 2.9, 4.6, 1.3],
    [4.8, 3. , 1.4, 0.1],
    [6.4, 2.8, 5.6, 2.1],
    [6.8, 3.2, 5.9, 2.3],
    [5.7, 4.4, 1.5, 0.4],
    [4.9, 3.1, 1.5, 0.1],
    [6.2, 3.4, 5.4, 2.3],
    [6.9, 3.1, 4.9, 1.5],
    [6.1, 2.8, 4.7, 1.2],
    [5. , 3.6, 1.4, 0.2],
    [5.7, 2.8, 4.5, 1.3],
    [7. , 3.2, 4.7, 1.4],
    [6. , 2.9, 4.5, 1.5],
    [4.8, 3. , 1.4, 0.3],
    [6.3, 2.3, 4.4, 1.3],
    [6.1, 3. , 4.9, 1.8],
    [5.7, 3. , 4.2, 1.2],
    [5.7, 2.8, 4.1, 1.3],
    [6.3, 2.5, 5. , 1.9],
    [4.4, 3.2, 1.3, 0.2],
    [6.7, 3. , 5. , 1.7],
    [6.9, 3.2, 5.7, 2.3],
    [5.4, 3. , 4.5, 1.5],
    [5. , 3. , 1.6, 0.2],
    [6.6, 3. , 4.4, 1.4],
    [5. , 3.3, 1.4, 0.2],
    [4.9, 2.4, 3.3, 1. ],
    [7.1, 3. , 5.9, 2.1]])

    array([[6.8, 3. , 5.5, 2.1],
    [7.9, 3.8, 6.4, 2. ],
    [6.4, 3.1, 5.5, 1.8],
    [5.3, 3.7, 1.5, 0.2],
    [4.6, 3.2, 1.4, 0.2],
    [5.2, 3.5, 1.5, 0.2],
    [6.5, 3.2, 5.1, 2. ],
    [6.3, 2.5, 4.9, 1.5],
    [6.7, 2.5, 5.8, 1.8],
    [4.9, 3.1, 1.5, 0.1],
    [5.8, 2.7, 3.9, 1.2],
    [5.4, 3.4, 1.5, 0.4],
    [6. , 2.2, 5. , 1.5],
    [6.7, 3.3, 5.7, 2.1],
    [5. , 3.5, 1.3, 0.3]])

    array([0, 1, 2, 0, 0, 1, 0, 2, 2, 2, 2, 0, 1, 1, 0, 2, 1, 2, 1, 1, 1, 1,
    2, 1, 0, 2, 0, 1, 1, 1, 2, 1, 1, 0, 1, 2, 1, 1, 0, 1, 2, 1, 2, 2,
    2, 1, 2, 2, 0, 0, 2, 1, 0, 2, 0, 1, 2, 2, 1, 0, 2, 0, 2, 0, 1, 2,
    0, 0, 1, 0, 2, 2, 0, 2, 0, 2, 2, 2, 1, 1, 0, 2, 0, 2, 0, 2, 1, 1,
    1, 0, 0, 0, 0, 0, 1, 0, 2, 2, 1, 0, 0, 0, 2, 0, 1, 0, 1, 1, 0, 2,
    2, 0, 0, 2, 1, 1, 0, 1, 1, 1, 0, 1, 2, 1, 1, 2, 0, 1, 2, 1, 0, 1,
    0, 1, 2])

    array([2, 2, 2, 0, 0, 0, 2, 1, 2, 0, 1, 0, 2, 2, 0])

Iris Setosa（山鸢尾）、Iris Versicolour（杂色鸢尾），
以及Iris Virginica（维吉尼亚鸢尾）

# 进行机器学习
from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier(n_neighbors=10)
# 空间复杂度  时间复杂度
knn.fit(X_train, y_train)

  • 输出

    KNeighborsClassifier(algorithm=’auto’, leaf_size=30, metric=’minkowski’,
    metric_params=None, n_jobs=1, n_neighbors=10, p=2,
    weights=’uniform’)

# 预测
knn.predict(X_test)

  • 输出

    array([2, 2, 2, 0, 0, 0, 2, 1, 2, 0, 1, 0, 2, 2, 0])

y_test

  • 输出

    array([2, 2, 2, 0, 0, 0, 2, 1, 2, 0, 1, 0, 2, 2, 0])

# 进行打分
knn.score(X_test, y_test)

  • 输出

    1.0

人体动作识别

练习
人类动作识别
步行，上楼，下楼，坐着，站立和躺着

练习

人类动作识别
步行，上楼，下楼，坐着，站立和躺着

数据采集每个人在腰部装着智能手机，进行了六个活动（步行，上楼，下楼，坐着，站立和躺着）。采用嵌入式加速度计和陀螺仪，以50Hz的恒定速度捕获3轴线性加速度和3轴(3维空间的XYZ轴)角速度(时间转一圈多少时间)，来获取数据
我们导入几个包x_test.npy x_train.npy y_test.npy y_train.npy ,这些都是numpy保存的数据
练习numpy怎么保存数据的

nd = np.random.randint(0,150, size=(5, 4))
nd

  • 输出

    array([[115, 145, 90, 131],
    [ 59, 125, 78, 136],
    [ 83, 2, 91, 93],
    [ 74, 68, 44, 92],
    [ 64, 145, 36, 90]])

# numpy的文件默认尾缀名为.npy
np.save('./nd_data.npy',nd)
# 加载npy的文件
np.load('./nd_data.npy')

  • 输出

    array([[115, 145, 90, 131],
    [ 59, 125, 78, 136],
    [ 83, 2, 91, 93],
    [ 74, 68, 44, 92],
    [ 64, 145, 36, 90]])

导入动作识别的包

label = {1:'WALKING', 2:'WALKING UPSTAIRS', 3:'WALKING DOWNSTAIRS',4:'SITTING', 5:'STANDING', 6:'LAYING'}
X_train = np.load('./knn_test/x_train.npy')
y_train = np.load('./knn_test/y_train.npy')
X_test = np.load('./knn_test/x_test.npy')
y_test = np.load('./knn_test/y_test.npy')
X_train.shape

  • 输出

    (7352, 561)

y_train.shape

  • 输出

    (7352,)

# 图形来表示动作
import matplotlib.pyplot as plt

plt.plot(X_train[1111])
# 加标题
plt.title(label[y_train[1111]])

  • 输出

    Text(0.5,1,’WALKING DOWNSTAIRS’)

这里写图片描述

# 进行数据训练，机器的学习
knn = KNeighborsClassifier(n_neighbors=15)
knn.fit(X_train, y_train)

  • 输出

    KNeighborsClassifier(algorithm=’auto’, leaf_size=30, metric=’minkowski’,
    metric_params=None, n_jobs=1, n_neighbors=15, p=2,
    weights=’uniform’)

# 开始进行预测
y_ = knn.predict(X_test)
y_

  • 输出

    array([5, 5, 5, …, 2, 2, 1], dtype=int64)

# 目标值
y_test

  • 输出

    array([5, 5, 5, …, 2, 2, 2], dtype=int64)

# 计算打分
knn.score(X_test, y_test)

  • 输出

    0.9043094672548354

# 人的动作对于机器来说就是频率，只要是频率都可以画图
# 将y_预测的数据对比y_test， 将这个答案作为标题
# argwhere(y_test == 1)
np.argwhere(y_test == 1).reshape(-1)

  • 输出

    array([ 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89,
    90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100,
    101, 102, 103, 104, 105, 106, 107, 108, 227, 228, 229,
    230, 231, 232, 233, 234, 235, 236, 237, 238, 239, 240,
    241, 242, 243, 244, 245, 246, 247, 248, 249, 250, 251,
    252, 253, 254, 255, 384, 385, 386, 387, 388, 389, 390,
    391, 392, 393, 394, 395, 396, 397, 398, 399, 400, 401,
    402, 403, 404, 405, 406, 407, 408, 409, 410, 411, 412,
    413, 414, 544, 545, 546, 547, 548, 549, 550, 551, 552,
    553, 554, 555, 556, 557, 558, 559, 560, 561, 562, 563,
    564, 565, 566, 567, 568, 569, 570, 571, 572, 690, 691,
    692, 693, 694, 695, 696, 697, 698, 699, 700, 701, 702,
    703, 704, 705, 706, 707, 708, 709, 710, 711, 712, 713,
    714, 715, 837, 838, 839, 840, 841, 842, 843, 844, 845,
    846, 847, 848, 849, 850, 851, 852, 853, 854, 855, 856,
    857, 858, 859, 860, 861, 862, 985, 986, 987, 988, 989,
    990, 991, 992, 993, 994, 995, 996, 997, 998, 999, 1000,
    1001, 1002, 1003, 1004, 1005, 1006, 1007, 1008, 1009, 1010, 1011,
    1132, 1133, 1134, 1135, 1136, 1137, 1138, 1139, 1140, 1141, 1142,
    1143, 1144, 1145, 1146, 1147, 1148, 1149, 1150, 1151, 1152, 1153,
    1154, 1155, 1156, 1157, 1283, 1284, 1285, 1286, 1287, 1288, 1289,
    1290, 1291, 1292, 1293, 1294, 1295, 1296, 1297, 1298, 1299, 1300,
    1301, 1302, 1303, 1304, 1305, 1306, 1307, 1308, 1309, 1452, 1453,
    1454, 1455, 1456, 1457, 1458, 1459, 1460, 1461, 1462, 1463, 1464,
    1465, 1466, 1467, 1468, 1469, 1470, 1471, 1472, 1473, 1474, 1605,
    1606, 1607, 1608, 1609, 1610, 1611, 1612, 1613, 1614, 1615, 1616,
    1617, 1618, 1619, 1620, 1621, 1622, 1623, 1624, 1625, 1626, 1627,
    1628, 1629, 1630, 1631, 1632, 1633, 1634, 1777, 1778, 1779, 1780,
    1781, 1782, 1783, 1784, 1785, 1786, 1787, 1788, 1789, 1790, 1791,
    1792, 1793, 1794, 1795, 1796, 1797, 1798, 1799, 1800, 1801, 1802,
    1803, 1950, 1951, 1952, 1953, 1954, 1955, 1956, 1957, 1958, 1959,
    1960, 1961, 1962, 1963, 1964, 1965, 1966, 1967, 1968, 1969, 1970,
    1971, 1972, 1973, 1974, 1975, 1976, 1977, 1978, 2129, 2130, 2131,
    2132, 2133, 2134, 2135, 2136, 2137, 2138, 2139, 2140, 2141, 2142,
    2143, 2144, 2145, 2146, 2147, 2148, 2149, 2150, 2151, 2152, 2153,
    2154, 2155, 2317, 2318, 2319, 2320, 2321, 2322, 2323, 2324, 2325,
    2326, 2327, 2328, 2329, 2330, 2331, 2332, 2333, 2334, 2335, 2336,
    2337, 2338, 2339, 2340, 2341, 2342, 2343, 2494, 2495, 2496, 2497,
    2498, 2499, 2500, 2501, 2502, 2503, 2504, 2505, 2506, 2507, 2508,
    2509, 2510, 2511, 2512, 2513, 2514, 2515, 2516, 2517, 2669, 2670,
    2671, 2672, 2673, 2674, 2675, 2676, 2677, 2678, 2679, 2680, 2681,
    2682, 2683, 2684, 2685, 2686, 2687, 2688, 2689, 2690, 2691, 2692,
    2693, 2694, 2695, 2696, 2859, 2860, 2861, 2862, 2863, 2864, 2865,
    2866, 2867, 2868, 2869, 2870, 2871, 2872, 2873, 2874, 2875, 2876,
    2877, 2878, 2879, 2880, 2881, 2882, 2883, 2884, 2885, 2886, 2887,
    2888], dtype=int64)

# 用循环来取值
plt.figure(figsize=(2*6, 3*5))
for i in range(6):
    # subplot第三个编号不能为0
    axes = plt.subplot(3, 2, i+1)
    np_index = np.argwhere(y_test == i + 1).reshape(-1)
    # 每个动作只取一个样本
    index = np_index[np.random.randint(0, np_index.size, size=1)[0]]

    axes.plot(X_test[index])
    # 给每张图片添加2个标题，分别是真实的答案，预测答案，但是只能用一个title,h换行、n
    axes.set_title('True:%s\n Predict:%s'%(label[y_test[index]], label[y_[index]]))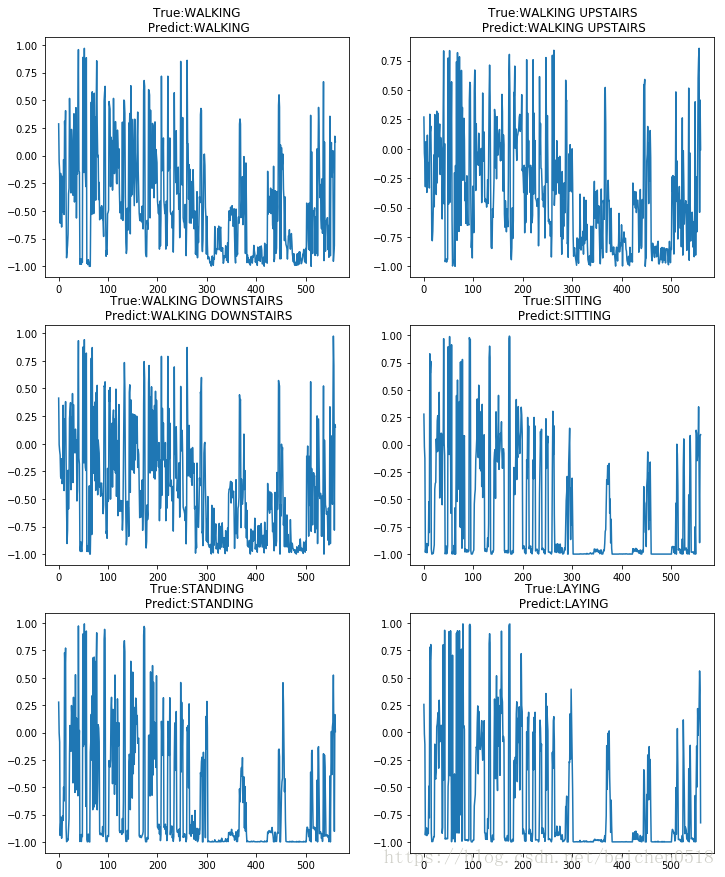

png

手写数字识别

#导入包
import numpy as np
import matplotlib.pyplot as plt
#引入机器学习
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
#黑白图片
#2维的

zero = plt.imread('./knn_num_data/0/0_1.bmp')
zero.shape

  • 输出

    (28, 28)

plt.figure(figsize=(2,2))
plt.imshow(zero,cmap='gray')
<matplotlib.image.AxesImage at 0xada0828>

这里写图片描述

#怎么读取图片?
#用循环
#这是我们手动拼接的公用路径
path = './knn_num_data/%d/%d_%d.bmp'
data = []
target = []
#有10个目录
for i in range(10):
    #下个循环500次,每个目录有500张图片
    for j in range(500):
        im_data = plt.imread(path%(i,i,j+1))
        data.append(im_data)
        target.append(i)
data = np.array(data)
data

  • 输出

    array([[[255, 255, 255, …, 255, 255, 255],
    [255, 255, 255, …, 255, 255, 255],
    [255, 255, 255, …, 255, 255, 255],
    …,
    [255, 255, 255, …, 255, 255, 255],
    [255, 255, 255, …, 255, 255, 255],
    [255, 255, 255, …, 255, 255, 255]],

       [[255, 255, 255, ..., 255, 255, 255],
    [255, 255, 255, ..., 255, 255, 255],
    [255, 255, 255, ..., 255, 255, 255],
    ...,
    [255, 255, 255, ..., 255, 255, 255],
    [255, 255, 255, ..., 255, 255, 255],
    [255, 255, 255, ..., 255, 255, 255]],

   [[255, 255, 255, ..., 255, 255, 255],
    [255, 255, 255, ..., 255, 255, 255],
    [255, 255, 255, ..., 255, 255, 255],
    ...,
    [255, 255, 255, ..., 255, 255, 255],
    [255, 255, 255, ..., 255, 255, 255],
    [255, 255, 255, ..., 255, 255, 255]],

   ...,

   [[255, 255, 255, ..., 255, 255, 255],
    [255, 255, 255, ..., 255, 255, 255],
    [255, 255, 255, ..., 255, 255, 255],
    ...,
    [255, 255, 255, ..., 255, 255, 255],
    [255, 255, 255, ..., 255, 255, 255],
    [255, 255, 255, ..., 255, 255, 255]],

   [[255, 255, 255, ..., 255, 255, 255],
    [255, 255, 255, ..., 255, 255, 255],
    [255, 255, 255, ..., 255, 255, 255],
    ...,
    [255, 255, 255, ..., 255, 255, 255],
    [255, 255, 255, ..., 255, 255, 255],
    [255, 255, 255, ..., 255, 255, 255]],

   [[255, 255, 255, ..., 255, 255, 255],
    [255, 255, 255, ..., 255, 255, 255],
    [255, 255, 255, ..., 255, 255, 255],
    ...,
    [255, 255, 255, ..., 255, 255, 255],
    [255, 255, 255, ..., 255, 255, 255],
    [255, 255, 255, ..., 255, 255, 255]]], dtype=uint8)

target = np.array(target)
target

  • 输出

    array([0, 0, 0, …, 9, 9, 9])

display(data.shape,target.size)
  • 输出
    (5000, 28, 28)
    5000
#现在的data是一个三维的,但是训练和预测数据只能是二维的?
data = data.reshape(5000,-1)
data.shape

  • 输出

    (5000, 784)

#要不要分开数据?
X_train,X_test,y_train,y_test=train_test_split(data,target,test_size=0.01)
#进行实例化
knn = KNeighborsClassifier(n_neighbors=5)
#训练
knn.fit(X_train,y_train)

  • 输出

    KNeighborsClassifier(algorithm=’auto’, leaf_size=30, metric=’minkowski’,
    metric_params=None, n_jobs=1, n_neighbors=5, p=2,
    weights=’uniform’)

#预测
y_ = knn.predict(X_test)
y_

  • 输出

    array([0, 2, 1, 3, 9, 8, 0, 4, 7, 5, 0, 8, 9, 3, 3, 2, 5, 5, 9, 8, 6, 9,
    0, 0, 9, 0, 0, 3, 8, 0, 3, 0, 4, 3, 5, 7, 0, 3, 0, 9, 8, 7, 9, 6,
    1, 5, 0, 3, 2, 2])

y_test

  • 输出

    array([0, 2, 8, 3, 9, 8, 0, 4, 7, 5, 0, 8, 9, 5, 3, 2, 5, 5, 9, 8, 6, 9,
    0, 0, 9, 0, 0, 3, 8, 0, 3, 0, 4, 3, 5, 3, 0, 3, 0, 9, 8, 7, 9, 6,
    5, 5, 0, 3, 2, 2])

#得分
knn.score(X_test,y_test)

  • 输出

    0.92

画图

我们预测了50个手写数字,将这50个数字的图片给展示出来,将真实的目标值和预测的值作为标题

 y_test[11]

  • 输出

    8

##### 循环
plt.figure(figsize=(5*2,10*3))
for i in range(50):
    axes = plt.subplot(10,5,i+1)
    #X_test 784
    axes.imshow(X_test[i].reshape(28,28))
    #给标题
    t = y_test[i]
    p = y_[i]
    #设置标题
    axes.set_title('True:%s\nPredict:%s'%(t,p))
    axes.axis('off')

这里写图片描述

plt.imshow(X_test[4].reshape(28,28))
<matplotlib.image.AxesImage at 0xb728a90>

这里写图片描述

#读取网上的图片
num = plt.imread('./num_.jpg')
plt.imshow(num)
<matplotlib.image.AxesImage at 0xc2e2a90>

这里写图片描述

z = num[3:65,3:65]
plt.imshow(z)
<matplotlib.image.AxesImage at 0xc441f98>

这里写图片描述

z.shape
  • 输出
    (62, 62, 3)
#降维
z = z.mean(axis=-1)
z.shape

  • 输出

    (62, 62)

#(28,28)
import cv2
#ndimage.zoom()
#cv2.resize()
z = cv2.resize(z,(28,28))
z.shape

  • 输出

    (28, 28)

#二维
x_test = np.array([z.reshape(-1)])
knn.predict(x_test)
  • 输出
    array([0])

换脸

import os, math
import cv2
from PIL import Image, ImageDraw
import matplotlib.pyplot as plt
# 1.将图片引入
sanpang = cv2.imread('./jinzhengen.png')
sanpang.shape

  • 输出

    (273, 411, 3)

guobin = cv2.imread('./guobin.jpg')
guobin.shape

  • 输出

    (405, 259, 3)

# 加载面部识别的算法
face_detect = cv2.CascadeClassifier('./haarcascade_frontalface_default.xml')
sanpang_face = face_detect.detectMultiScale(sanpang)
guobin_face = face_detect.detectMultiScale(guobin)
display(sanpang_face, guobin_face)
  • 输出
    array([[182, 62, 61, 61]], dtype=int32)
    array([[ 32, 82, 164, 164]], dtype=int32)
# sanpang 的脸替换得到guobin的脸上
# 将三胖的脸切圆
# 先要获取到脸部的图片
for x, y, w, h in sanpang_face:
    sface = sanpang[y:y + h, x:x + w]
# guobin的脸
for x, y, w, h in guobin_face:
    gface = guobin[y:y + h, x:x + w]
plt.imshow(gface[:,:,::-1])
<matplotlib.image.AxesImage at 0xc408e10>

sface = cv2.resize(sface, (164, 164))
plt.imshow(sface[:,:,::-1])
<matplotlib.image.AxesImage at 0xa202160>

# 把脸给它保存成图片
spath = './sface.png'
gpath = './gface.jpg'
new_path = './new_face.png'
cv2.imwrite(spath,sface)
cv2.imwrite(gpath,gface)

  • 输出

    True

# a_path 代表要切圆的图片；b_path代表填补数据
def circle(a_path, b_path, new_path):
    # A alpha 代表透明度
    ima = Image.open(a_path).convert("RGBA")

    size = ima.size

    # 因为是要圆形,所以需要正方形的图片

    r2 = min(size[0], size[1])

    if size[0] != size[1]:
        # 抗锯齿
        ima = ima.resize((r2, r2), Image.ANTIALIAS)
    # 重新创建一个白色，画布
    imb = Image.new('RGBA', (r2, r2),(255,255,255,0))
    imc = Image.open(b_path).convert("RGBA")
    pima = ima.load()

    pimb = imb.load()

    pimc = imc.load()

    r = float(r2/2) #圆心横坐标

    for i in range(r2):

        for j in range(r2):

            lx = abs(i-r+0.5) #到圆心距离的横坐标

            ly = abs(j-r+0.5)#到圆心距离的纵坐标

            l  = pow(lx,2) + pow(ly,2)

            if l <= pow(r, 2):

                pimb[i,j] = pima[i,j]
            else:
                pimb[i,j] = pimc[i,j]

    imb.save(new_path)
circle(spath, gpath, new_path)
# 原图是什么格式打开就是什么格式
trans = plt.imread(new_path)
# 将图片转化为jpg打开，并且是rgb,而不是rgba
trans = cv2.imread(new_path)
trans.shape

  • 输出

    (164, 164, 3)

trans = trans[:,:,:-1]
trans.shape

  • 输出

    (164, 164, 3)

plt.imshow(trans)
<matplotlib.image.AxesImage at 0xeb60f98>

for x, y, w, h in guobin_face:
    guobin[y:y + h, x:x + w] = trans
plt.imshow(guobin[:,:,::-1])
<matplotlib.image.AxesImage at 0x97c0da0>
北辰0518
关注
KNN手写数字识别（记录）
zyoulanxin的博客
08-13 312
import numpy as np import os from os import listdir import operator def classify0(inX,dataSet,labels,k): dataSetSize = dataSet.shape[0] diffMat = np.tile(inX,(dataSetSize,1))-dataSet sqDiffMat = diffMat**2 sqDistances = sqDiffMat.sum(axis=
knn实现手写数字识别
mossxzzom的博客
10-04 824
使用knn训练数据 knn原理为某个样本在空间中的k个最近的样本中的最多数属于某一个类别。将数据集分为训练集与测试集两部分 测试集用于训练生成的模型的准确率 其比例为8:2。投票算法使用少数服从多数 y表示target sum表示vote数量。这里使用的是sklearn官方的数据集 导入比较简单。上述代码选择了最大的vote作为预测结果。对于训练集每个点使用下述方式计算距离。公式用python表达也非常简单。取前两个预测数据和测试数据比较下。对于knn距离使用欧拉距离。手写数字识别数据集。
kNN —— 手写数字识别
birdguan
02-21 325
这里手写数据的数据集并不是大家熟知的MNIST，而是土耳其伊斯坦布尔海峡大学计算机工程系的E.Alpaydin与C.Kaynak的数据集，地址： http://archive.ics.uci.edu/ml 每一个数字为 黑白图像，如下图所示：   程序如下： import numpy as np import os import operator def img2vector(...
KNN手写数字识别
zhuyi_zi的博客
11-17 699
以欧几里得距离度量样本间的相识程度。对于一个测试样本首先计算该样本与每个训练样本间的距离，然后以距离值进行升序排序，排序够前K个样本进行投票，即那个标签出现的次数多，就将该测试样例划为该类。        程序使用数据来源http://yann.lecun.com/exdb/mnist/。预先将数据处理为图片，标签信息转化为txt文档。 from numpy import * import n
KNN算法：原理、实现与评估
最新发布
AgiaozzZ的博客
10-30 681
KNN算法作为机器学习中最基础的分类算法之一，其简单直观的原理和实现方式使其成为初学者学习机器学习的理想起点。通过合理选择K值、进行特征标准化、使用合适的距离度量，可以有效提升KNN的分类性能。在模型评估方面，应避免仅依赖准确率，而应结合混淆矩阵、ROC曲线、PR曲线等多维度指标进行综合评估。对于类别不平衡问题，F1分数和PR曲线是更合适的评估指标。尽管KNN存在计算复杂度高等局限性，但通过适当的调优和特征工程，它在许多实际应用场景中仍能发挥重要作用。
KNN识别手写数字
dianwei0041的博客
06-30 424
一、问题描述 手写数字被存储在EXCEL表格中，行表示一个数字的标签和该数字的像素值，有多少行就有多少个样本。 一共42000个样本 二、KNN KNN最邻近规则，主要应用领域是对未知事物的识别，即判断未知事物属于哪一类，判断思想是，基于欧几里得定理，判断未知事物的特征和哪一类已知事物的的特征最接近； K最近邻(k-Nearest Neighbor，KNN)分类...
knn 1.12.0压缩包
12-27
KNN，即K-最近邻算法，是一种基本分类与回归方法。它通过对距离的计算，找出与待分类数据距离最近的K个邻居，并根据这些邻居的类别和距离权重来进行分类。在机器学习和数据挖掘领域，KNN算法因其简单性和有效性而被...
精选资源
KNN_KNN分类_CIFAR-10_knn图像分类
09-11
KNN（K-Nearest Neighbors）算法是一种监督学习方法，常用于分类和回归问题，尤其在图像分类中表现出色。CIFAR-10是一个广泛使用的图像识别数据集，包含10个类别的60000张32x32像素的彩色图像。本项目将KNN算法应用...
精选资源
KNN进行水果分类和分类器实战.docx
10-09
【KNN算法简介】 K-Nearest Neighbor (KNN) 算法是机器学习领域中最基础的算法之一，适用于分类和回归任务。KNN基于实例的学习，它并不需要进行显式的模型训练，而是直接根据已有数据进行预测。在分类问题中，KNN...
elastiknn7.17.23.0版本 elsaticsearch7.17.23版本knn搜索插件
07-30
它将高效的 k-Nearest Neighbors (kNN) 算法集成到 Elasticsearch 中，支持对高维向量（如 Embedding 向量）进行实时检索，适用于 AI 驱动场景（语义搜索、图像检索、推荐系统等）。 发现官网到7.17.9就停止更新了。...
Python实现KNN时间序列预测（完整源码和数据)
04-08
1.Python实现KNN时间序列预测（完整源码和数据) anaconda + pycharm + python +Tensorflow 注意事项：保姆级注释，几乎一行一注释，方便小白入门学习！ 2.代码特点：参数化编程、参数可方便更改、代码编程思路清晰、...
KNN实现手写数字识别
03-28
基于opencv-KNN最邻近算法实现手写数字识别，使用Qt做UI实现手写板，可以实时测试，资源包含源代码和可执行程序（release文件夹下的exe文件可以直接运行）
knn 进行手写数字识别
人工智能
08-17 268
数据集使用了Keras的datasets from sklearn.neighbors import KNeighborsClassifier from sklearn.metrics import classification_report from keras.datasets import mnist (x_train_tmp, y_train_tmp), (x_test_tmp, y_test_tmp) = mnist.load_data() x_test_new = x_test_tmp.r
基于KNN的手写数字识别
zj572459439的专栏
06-14 1146
实现了基于KNN的手写数字识别
用 KNN 做手写数字识别
caizhengye的博客
07-22 1708
用 KNN 做手写数字识别 目录 用 KNN 做手写数字识别 1. KNN的原理 2. KNN实现手写数字识别过程 作为一个小白，写此文章主要是为了自己记录，方便回过头来查找！ 本文主要参考ApacheCN（专注于优秀项目维护的开源组织）中MachineLearning中的KNN项目。有些代码参考这个项目（大部分），有些代码是自己写的。建议去ApacheCN去学习，还有专门的视频讲解，个...
knn
05-17
### KNN算法简介 KNN算法（K-Nearest Neighbor Algorithm）是一种基础的机器学习方法，广泛应用于分类和回归任务中。其核心思想是基于距离度量寻找与目标样本最接近的K个邻居，并利用这些邻居的信息来进行预测[^1]。 在实际操作中，KNN算法通过计算新输入样本与已有数据集中每个样本的距离，找出最近的K个样本作为参考依据。对于分类问题，通常采用多数投票法决定类别归属；而对于回归问题，则取这K个样本的目标值均值作为预测结果[^2]。 #### 算法特点 - **优点**: - 实现简单直观，易于理解和实现。 - 对于多分类问题具有良好的适应能力。 - 能够有效处理非线性分布的数据集。 - **缺点**: - 计算开销较大，尤其当数据规模增大时，每次查询都需要遍历整个训练集并计算距离。 - 敏感于特征缩放以及噪声干扰，在预处理阶段需特别注意标准化等问题。 ### KNN算法的应用领域 由于其实用性和灵活性,KNN被成功运用于多个技术方向: 1. **图像识别** 图像可以通过像素矩阵形式表达,每张图片视为独立向量点.KNN通过对未知图象同数据库里存储的标准样例做对比分析从而判定所属种类.[^1] 2. **语音信号处理** 类似地,音频文件也能转换成频谱序列或者其他数字化描述方式之后交给KNN完成辨识工作. 3. **自然语言处理(NLP)** 文档主题建模或者情感倾向判断都可以借助此手段达成目的之一就是先提取关键词频率统计之类的量化指标再送入模型内部运算得到最终结论. 4. **个性化推荐引擎开发** 用户行为习惯记录下来形成庞大的历史资料库以后就可以运用类似的原理推测可能感兴趣的商品列表呈现出来供浏览选购考虑了. 以下是简单的Python代码演示如何使用scikit-learn库快速搭建一个基本版别的knn分类器实例： ```python from sklearn.datasets import load_iris from sklearn.model_selection import train_test_split from sklearn.preprocessing import StandardScaler from sklearn.neighbors import KNeighborsClassifier from sklearn.metrics import accuracy_score # 加载鸢尾花数据集 data = load_iris() X, y = data.data, data.target # 划分训练集与测试集 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42) # 数据标准化 scaler = StandardScaler() X_train_scaled = scaler.fit_transform(X_train) X_test_scaled = scaler.transform(X_test) # 初始化KNN分类器(k设为5) clf = KNeighborsClassifier(n_neighbors=5) clf.fit(X_train_scaled, y_train) # 进行预测 y_pred = clf.predict(X_test_scaled) # 输出准确率 print(f'Accuracy: {accuracy_score(y_test, y_pred):.2f}') ```
评论
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值