北邮22信通一枚~
跟随课程进度更新北邮信通院DSP的笔记、代码和文章,欢迎关注~
获取更多文章,请访问专栏:
目录
3.3.2DSP中的“倒置”和程序中的“倒置”矛盾与解决方法
1.定义


2.求解方法(通过实例讲解)
求解DFT的循环卷积有三种方法,分别是同心圆法、波形图法和解析式法。
例题:
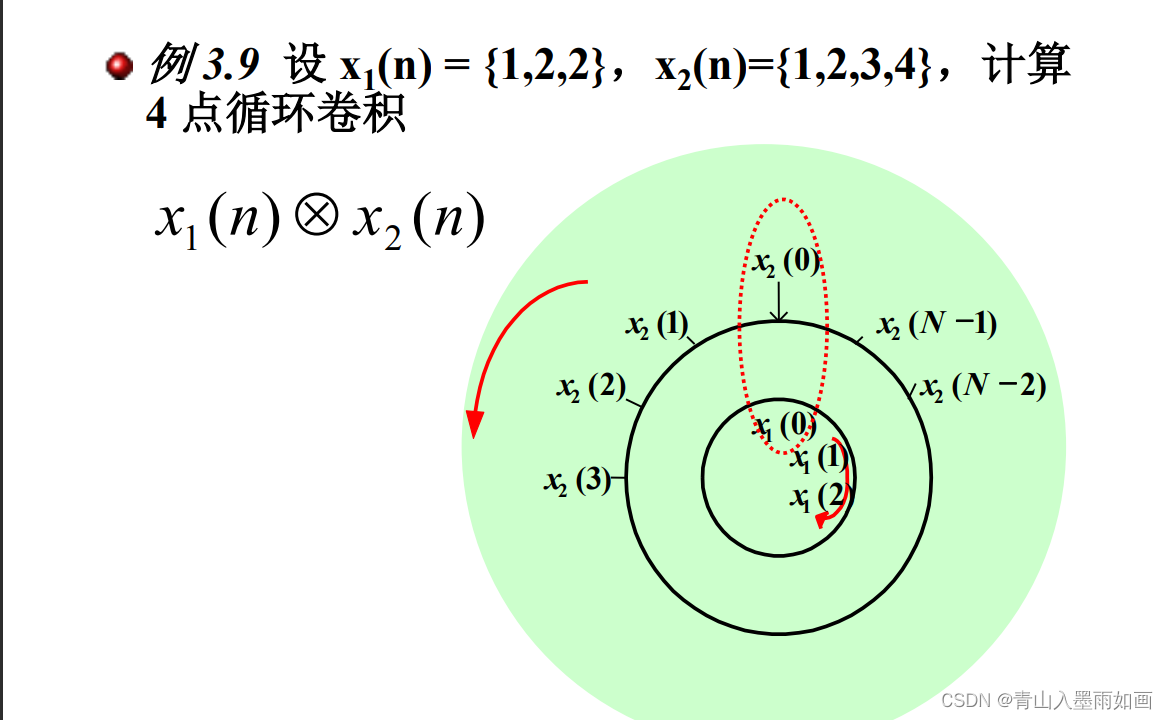
同心圆解法




3.程序思维分析

注:这里的“倒置”是“程序倒置”,而不是DSP中规定的序列倒置,详情请参考下文
3.3.2DSP中的“倒置”和程序中的“倒置”矛盾与解决方法
3.1选择存储结构
其中,序列的存储和计算可以使用队列结构,综合考虑需要进行倒置操作,最终选定双向队列实现。
3.2双向队列的优点
3.2.1.自然倒置
如果使用普通队列,就涉及队列倒置函数的书写,其中时间复杂度至少为n;而使用双向队列可以从不同的方向输入,如果从队列头部开始输入,则在输入过程中就已经自然地实现了队列的倒置操作。
3.2.2.快速头插
如果使用普通队列,在队列头部添加元素是件很繁琐的工程,而双向队列有相应的内置函数,简便地完成头插操作。
3.3实现过程分析
3.3.1.补零操作
在DSP中,如果两个序列的长度小于要计算的卷积点数,需要进行补零操作。
补零操作之后,第二个序列才会进行倒置。
所以,对第一个序列(不用进行倒置的序列),直接采用双向队列的尾插法补零即可。
对第二个序列(需要进行倒置的序列),倒置之后直接采用双向队列的头插法补零即可。
3.3.2DSP中的“倒置”和程序中的“倒置”矛盾与解决方法
按照DSP的观点,序列x(n)= {1,2,3,4}的倒置应为x(-n)= {1,4,3,2};
而程序中倒置{1,2,3,4}的结果为{4,3,2,1};
所以在用程序实现之前,需要先进行一步移位操作。
多举几个例子:
DSP中序列x(n)= {1,2,3,4,0}的倒置应为x(-n)= {1,0,4,3,2};
而程序中倒置{1,2,3,4,0}的结果为{0,4,3,2,1};
所以在用程序实现之前,需要先进行一步移位操作。
3.3.3移位与计算
补零、倒置之后两个序列长度相等。对应项相乘在相加,得到结果序列中的第一个元素。第二个序列再次将头元素移动到队列末尾构成新序列,重复上面的操作,得到结果序列的第二个元素。
重复上面过程,最终输出结果。
3.3.4汇总
第一个序列尾插法输入;
第二个序列头插法输入(实现了程序倒置,但还没有成为DSP倒置);//{0,4,3,2,1}
补零操作;
第二个序列移位一次(这里才真正意义上完成了第一次DSP倒置);//{1,0,4,3,2}
两个序列对应项相乘,结果相加,尾插入结果序列;
第二个序列移位一次;
两个序列对应项相乘,结果相加,尾插入结果序列;//{2,1,0,4,3}
……
输出结果序列。
3.3.5多点循环卷积的更多例子

4.代码部分
4.1代码部分
#include<iostream>
#include<deque>
#include<cmath>
using namespace std;
int deque_min;
int deque_max = 100;
void deque_print(deque<int>a)
{
cout << "打印队列如下:" << endl;
for (int i = 0; i < a.size(); i++)
{
cout << a.front() << " ";
a.push_back(a.front());
a.pop_front();
}
cout << endl;
}
void destruction(deque<int>&a)
{
while(!a.empty())
a.pop_back();
}
int main()
{
system("color 0A");
deque<int>a, b, rtn;
int input, cnt_a = 0, cnt_b = 0, temp_sum = 0;
cout << "请问您想从几点卷积开始计算?" << endl;
cin >> deque_min;
cout << "请问您想终止于几点卷积?" << endl;
cin >> deque_max;
cout << "请输入周期卷积序列1:" << endl;
while (cin >> input)
{
a.push_back(input);
cnt_a++;
if (getchar() == '\n')break;
}
cout << "请输入周期卷积序列2:" << endl;
while (cin >> input)
{
b.push_front(input);
cnt_b++;
if ((getchar() == '\n'))break;
}
//judge
if (cnt_a > deque_min || cnt_b > deque_min || deque_min > deque_max)
{
cout << "error" << endl;
return 0;
}
//calculate
cout << endl;
for(int i=deque_min;i<=deque_max;i++)
{
cout << i << "点卷积结果如下:" << endl;
//add zero to each one
while (cnt_a < i)
{
a.push_back(0);
cnt_a++;
}
while (cnt_b < i)
{
b.push_front(0);
cnt_b++;
}
//cyclic convolution
int cnt = i;
while (cnt--)
{
b.push_front(b.back());
b.pop_back();
for (int j = 0; j < i; j++)
{
temp_sum += (a.front() * b.front());
a.push_back(a.front()); b.push_back(b.front());
a.pop_front(); b.pop_front();
}
rtn.push_back(temp_sum);
temp_sum = 0;
}
//print
deque_print(a);
deque_print(b);
deque_print(rtn);
//destruct the result deque for next period of storage
destruction(rtn);
cout << endl;
}
return 0;
}4.2运行结果
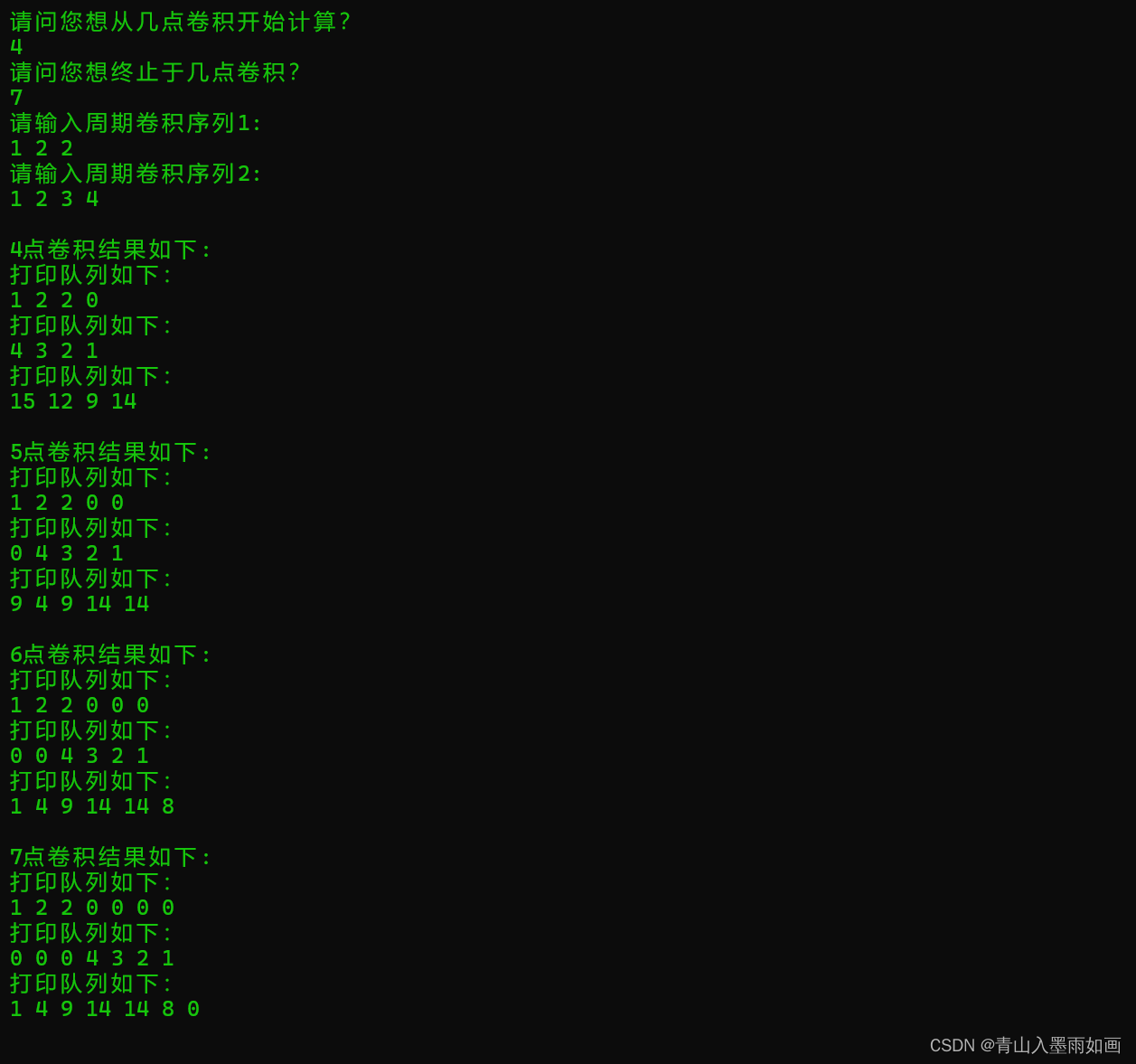





 本文详细介绍了在北邮信通院DSP课程中,如何通过实例讲解求解DFT的循环卷积问题,包括同心圆法、波形图法和解析式法,重点阐述了使用双向队列进行存储结构的选择及其优点,以及在程序中处理DSP中序列倒置与实际编程操作的差异。提供了C++代码示例以展示计算过程。
本文详细介绍了在北邮信通院DSP课程中,如何通过实例讲解求解DFT的循环卷积问题,包括同心圆法、波形图法和解析式法,重点阐述了使用双向队列进行存储结构的选择及其优点,以及在程序中处理DSP中序列倒置与实际编程操作的差异。提供了C++代码示例以展示计算过程。


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










