机器学习笔记 - 行列式

一、概述

        矩阵可以看作是空间的线性变换。矩阵A的行列式是一个数字，对应于使用该矩阵变换空间时获得的乘法变化。负行列式意味着方向发生了变化（而不仅仅是重新缩放和/或旋转）。方向的变化意味着例如在2D平面中，进行镜像。

        这是一个区分正行列式和负行列式的示例：

矩阵的行列式描述该矩阵相关的变换的信息

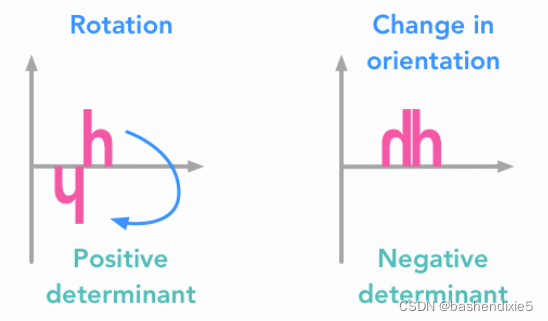
        可以看到，通过旋转和缩放无法获得负行列式对应的变换。

        此外，行列式还为您提供了转换量。 如果你取n维单位立方体并在其上应用矩阵A，则行列式的绝对值对应于变换后图形的面积。

二、例1

        为了计算形状的面积，我们将使用二维的简单正方形。 单位平方面积可