序设计思维与实践 CSP-M4

A:

题意：
题目描述 这一天，TT因为疫情在家憋得难受，在云吸猫一小时后，TT决定去附近自家的山头游玩。
TT来到一个小湖边，看到了许多在湖边嬉戏的鸭子，TT顿生羡慕。此时他发现每一只鸭子都不 一样，或羽毛不同，或性格不同。TT在脑子里开了一个map<鸭子，整数> tong，把鸭子变成了 一些数字。现在他好奇，有多少只鸭子映射成的数的数位中不同的数字个数小于k。

输入描述
输入第一行包含两个数n,k，表示鸭子的个数和题目要求的k。
接下来一行有n个数,$a_i$，每个数表示鸭子被TT映射之后的值。

输出描述
输出一行，一个数，表示满足题目描述的鸭子的个数。
无行末空格
样例输入
6 5
123456789 9876543210 233 666 1 114514
样例输出
4
数据点

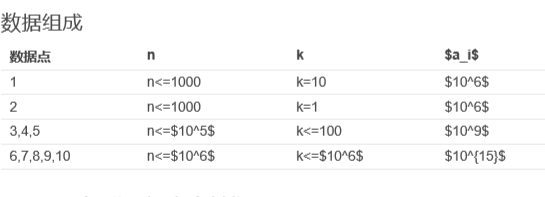
思路：
一开始看题目的时候，被数据点给唬住了，看到k的值可以如此大，一时间有点懵，总觉得自己的想法是错的，就这么耽误了很长时间。然后开始写的时候，觉得题目还行。然后提交的时候，发现没过，卡时间卡了四个点，我的天。然后看到说卡了stl，于是把set给去了，还是超时了，然后改用了scanf，并且读入的时候没有读数字了，直接读的字符串，这样的话，中间会少很多除法和取余计算。然后其实在k>10的时候可以处理以下直接跳过了。当然最终以900ms险过。

代码：

#include <iostream>
#include <string>
#include <cstring>
#include <cstdio>
#include <algorithm>
using namespace std;
int n, k, tot;
int flag[11];
char c[20];

int main() {
	tot = 0;
	scanf("%d%d",&n,&k);
	int len,num;
	while (n--){
		scanf("%s",c);
		num=0; 
		memset(flag,0,sizeof(flag));
		len=strlen(c);
		for(int i=0; i<len;i++){
			int tmp=c[i]-'0';
			if(flag[tmp]==0){
				flag[tmp]=1;
				num++;
			}
		}
		if(num<k) tot++;
	}
	cout<<tot;
	return 0;
}	

B

题目描述:
据传，2020年是宇宙射线集中爆发的一年，这和神秘的宇宙狗脱不了干系！但是瑞神和东东忙 于正面对决宇宙狗，宇宙射线的抵御工作就落到了ZJM的身上。假设宇宙射线的发射点位于一个 平面，ZJM已经通过特殊手段获取了所有宇宙射线的发射点，他们的坐标都是整数。而ZJM要构 造一个保护罩，这个保护罩是一个圆形，中心位于一个宇宙射线的发射点上。同时，因为大部分 经费都拨给了瑞神，所以ZJM要节省经费，做一个最小面积的保护罩。当ZJM决定好之后，东东 来找ZJM一起对抗宇宙狗去了，所以ZJM把问题扔给了你~

输入描述: 输入 第一行一个正整数N，表示宇宙射线发射点的个数
接下来N行，每行两个整数X,Y，表示宇宙射线发射点的位置

输出描述: 输出包括两行
第一行输出保护罩的中心坐标x,y 用空格隔开
第二行输出保护罩半径的平方
（所有输出保留两位小数，如有多解，输出x较小的点，如扔有多解，输入y较小的点）
无行末空格

样例输入
5
0 0
0 1
1 0
0 -1
-1 0

样例输出:
0.00 0.00
1.00

思路：
数据点不大，一开始想的是之前上课讲过的求图中的最大直径，觉得能圈住这整个的最小的半径一定要圈住这个最大直径。然后求出最大直径后的两点的时候，就遍历所有的点，求这些点能覆盖这两个最大直径上的点的最小的半径。但是错了，就过了两个点。因为点少，就暴力遍历每个点，求这个点到所有的点的距离的平方。求出能覆盖的最小的即可，同时，有如果相同的距离点后，则记录下x最小的，再者记录下y最小的，则可以在计算之前就对每个点进行这样的排序，这样就可以保证记录下的第一个点就符合这样的顺序的。

代码：

#include <iostream>
#include <string>
#include <cstring>
#include <cstdio>
#include <algorithm>
using namespace std;
int n, k, tot;
int flag[11];
char c[20];

int main() {
	tot = 0;
	scanf("%d%d",&n,&k);
	int len,num;
	while (n--){
		scanf("%s",c);
		num=0; 
		memset(flag,0,sizeof(flag));
		len=strlen(c);
		for(int i=0; i<len;i++){
			int tmp=c[i]-'0';
			if(flag[tmp]==0){
				flag[tmp]=1;
				num++;
			}
		}
		if(num<k) tot++;
	}
	cout<<tot;
	return 0;
}