【KMP】-优快云博客

什么是前缀表

写过KMP的同学，一定都写过next数组，那么这个next数组究竟是个啥呢？

next数组就是一个前缀表（prefix table）。

前缀表有什么作用呢？

前缀表是用来回退的，它记录了模式串与主串(文本串)不匹配的时候，模式串应该从哪里开始重新匹配。

为了清楚地了解前缀表的来历，我们来举一个例子：

要在文本串：什么是前缀表
写过KMP的同学，一定都写过next数组，那么这个next数组究竟是个啥呢？

next数组就是一个前缀表（prefix table）。

前缀表有什么作用呢？

首先要知道前缀表的任务是当前位置匹配失败，找到之前已经匹配上的位置，再重新匹配，此也意味着在某个字符失配时，前缀表会告诉你下一步匹配中，模式串应该跳到哪个位置

那么什么是前缀表：记录下标i之前（包括i）的字符串中，有多大长度的相同前缀后缀。

为了清楚地了解前缀表的来历，我们来举一个例子：
要在文本串：aabaabaafa 中查找是否出现过一个模式串：aabaaf。

请记住文本串和模式串的作用，对于理解下文很重要，要不然容易看懵。

要在文本串：aabaabaafa 中查找是否出现过一个模式串：aabaaf。

最长相等前后缀

前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串。

后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串。

前缀表要求的就是相同前后缀的长度。

前缀表

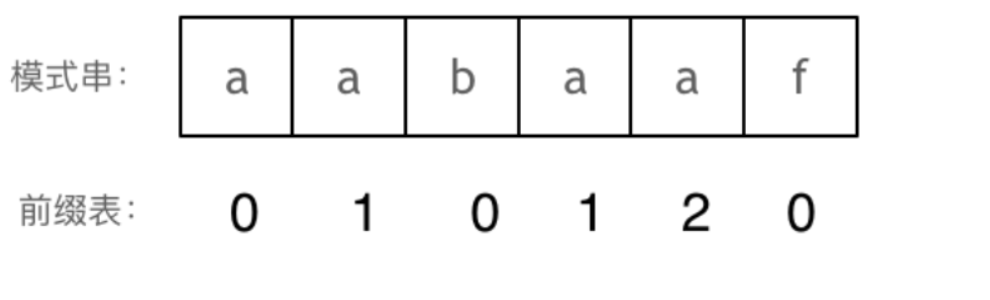
找到的不匹配的位置，那么此时我们要看它的前一个字符的前缀表的数值是多少。

为什么要前一个字符的前缀表的数值呢，因为要找前面字符串的最长相同的前缀和后缀。

所以要看前一位的前缀表的数值。

前一个字符的前缀表的数值是2，所以把下标移动到下标2的位置继续比配。可以再反复看一下上面的动画。

最后就在文本串中找到了和模式串匹配的子串了

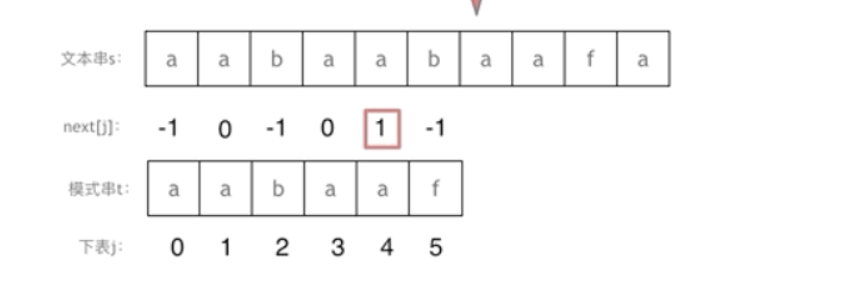
next数组

很多KMP算法的实现都是使用next数组来做回退操作，那么next数组与前缀表有什么关系呢？

next数组就可以是前缀表，但是很多实现都是把前缀表统一减一（右移一位，初始位置为-1）之后作为next数组。

为什么这么做呢，其实也是很多文章视频没有解释清楚的地方。

其实这并不涉及到KMP的原理，而是具体实现，next数组既可以就是前缀表，也可以是前缀表统一减一（右移一位，初始位置为-1）。

代码实现

-1

构造next数组其实就是计算模式串s，前缀表的过程。主要有如下三步：

1. 初始化
2. 处理前后缀不相同的情况
3. 处理前后缀相同的情况

初始化:
定义两个指针i和j，j指向前缀末尾位置，i指向后缀末尾位置。

int j=-1;
next[0]=j;

j 为什么要初始化为 -1呢，因为之前说过前缀表要统一减一的操作仅仅是其中的一种实现，我们这里选择j初始化为-1

next[i] 表示 i（包括i）之前最长相等的前后缀长度（其实就是j）
所以初始化next[0] = j 。

处理前后缀不相同的情况

因为j初始化为-1，那么i就从1开始，进行s[i] 与 s[j+1]的比较。
所以遍历模式串s的循环下标i 要从 1开始，代码如下：

for (int i = 1; i < s.size(); i++) {

如果 s[i] 与 s[j+1]不相同，也就是遇到前后缀末尾不相同的情况，就要向前回退。
怎么回退呢？
next[j]就是记录着j（包括j）之前的子串的相同前后缀的长度。
那么 s[i] 与 s[j+1] 不相同，就要找 j+1前一个元素在next数组里的值（就是next[j]）。
所以，处理前后缀不相同的情况代码如下：

while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
    j = next[j]; // 向前回退
}

处理前后缀相同的情况
如果 s[i] 与 s[j + 1] 相同，那么就同时向后移动i 和j 说明找到了相同的前后缀，同时还要将j（前缀的长度）赋给next[i], 因为next[i]要记录相同前后缀的长度。
代码如下：

void getNext(int* next, const string& s) {
  int j = -1;
  next[0] = j;
  for(int i = 1; i < s.size(); i++) {
    if (s[i] == s[j + 1]) {
      j++;
    }
    while (j >= 0 && s[i] != s[j + 1]) {
      j = next[j];
    }
    next[i] = j;
  }
}

使用next数组来做匹配

在文本串s里找是否出现过模式串t。

定义两个下标j 指向模式串起始位置，i指向文本串起始位置。

那么j初始值依然为-1，为什么呢？ **依然因为next数组里记录的起始位置为-1。**

i就从0开始，遍历文本串，代码如下：

for (int i = 0; i < s.size(); i++)

接下来就是 `s[i]`与 `t[j + 1]` （因为j从-1开始的）进行比较。
如果 `s[i]` 与 `t[j + 1]` 不相同，j就要从next数组里寻找下一个匹配的位置。
代码如下：

   // 当前字符不匹配时，通过next数组调整j的位置
    while (j >= 0 && s[i] != t[j + 1]) {
        j = next[j];
    }

如果 s[i] 与 t[j + 1] 相同，那么i 和 j 同时向后移动，代码如下：

    // 字符匹配时，移动模式串指针
    if (s[i] == t[j + 1]) {
        j++;
    }

如何判断在文本串s里出现了模式串t呢，如果j指向了模式串t的末尾，那么就说明模式串t完全匹配文本串s里的某个子串了。

本题要在文本串字符串中找出模式串出现的第一个位置 (从0开始)，所以返回当前在文本串匹配模式串的位置i 减去模式串的长度，就是文本串字符串中出现模式串的第一个位置。

代码如下：

if (j == (t.size() - 1)) { 
    return (i - t.size() + 1); 
}

条件判断：检查变量 j 是否等于 t.size() - 1，即是否到达目标字符串 t 的末尾。
返回值：若条件成立，返回 i - t.size() + 1，表示在主字符串中找到了完整匹配的子串起始位置。

前缀表数值

此时如果输入的模式串为aabaaf，对应的next为 0 1 0 1 2 0，（其实这就是前缀表的数值了）。

那么用这样的next数组也可以用来做匹配，代码要有所改动。

实现代码如下：

void getNext(int* next, const string& s) {
    int j = 0;
    next[0] = 0;
    for(int i = 1; i < s.size(); i++) {
        while (j > 0 && s[i] != s[j]) {
            j = next[j - 1];
        }
        if (s[i] == s[j]) {
            j++;
        }
        next[i] = j;
    }
}

getNext函数用于生成部分匹配表（next数组），记录模式串needle的前缀和后缀的最长公共长度。
j表示前缀末尾位置，i表示后缀末尾位置，通过比较s[i]和s[j]来更新next数组。

int strStr(string haystack, string needle) {
    if (needle.size() == 0) {
        return 0;
    }
    vector<int> next(needle.size());
    getNext(&next[0], needle);
    int j = 0;
    for (int i = 0; i < haystack.size(); i++) {
        while(j > 0 && haystack[i] != needle[j]) {
            j = next[j - 1];
        }
        if (haystack[i] == needle[j]) {
            j++;
        }
        if (j == needle.size()) {
            return (i - needle.size() + 1);
        }
    }
    return -1;
}