偏心同步磁阻电机快速建模

一种用于快速预测偏心同步磁阻电机磁场的非线性模型

摘要

本文提出了一种用于快速表征应用于电动汽车（ EVs）的同心和偏心同步磁阻电机（SynRMs）的新型数值模型。鉴于气隙和磁导函数对建模精度具有重要影响，采用阶跃变化函数来考虑磁通屏障对气隙的影响。随后，对包括静态偏心、动态偏心和混合偏心在内的不同类型的偏心率进行了建模。此外，该模型还考虑了磁饱和和定子槽效应。通过对电机电感进行数值计算，避免了磁导函数中的任何近似处理。进而计算了气隙磁通密度、电磁转矩以及转子上的径向力。该模型可用于同步磁阻电机（SynRMs）的初步设计，以分析电机在不同工况下的性能，并加快设计流程。该模型可方便地调整以适应不同的结构配置。例如，研究了一台4极单层分布绕组电机，其具有36槽和每极3个磁通屏障。为了验证所提出的模型，将所得结果与有限元分析 （FEA）和实验测试进行了对比。所提出的模型在偏心率达到 30%时的精度为98%，在更高偏心度下的精度约为95%。

索引词 — 电动汽车，同步磁阻电机，偏心率，磁通密度，有限元方法

I. 引言

电动机是电动汽车（EVs）的最重要部件之一。由于具备高转矩和高速度、宽速度范围以及高效率的特点，同步磁阻电机（SynRMs）在电动汽车应用中具有良好的潜力[1]。近年来，已开展了大量研究以提升SynRM在电动汽车中的性能[2-5]。同步磁阻电机基于磁阻原理产生转矩。它们采用类似于工业感应电机的传统定子结构。转子仅由硅钢片构成，并带有分布磁通屏障。为了提高安全性和降低维修成本，电动机应针对不同故障进行保护。偏心率有三种类型：静态偏心（SE）、动态偏心（DE）和混合偏心（ME）。在SE中，转子轴心与旋转轴重合，但偏离定子轴线。在DE中，定子轴线与旋转轴重合，而转子相对于定子轴线发生偏移。在DE中，与SE不同，最小气隙取决于转子位置。

在混合偏心中，转子、定子和旋转轴各不相同，且气隙随转子旋转而变化[6]。由于制造误差和轴承公差，实际电机中存在一定程度的偏心率。偏心率会产生电磁力，也称为不平衡磁拉力 （UMP），该力相互作用于转子与定子之间。不平衡磁拉力倾向于加剧偏心率，并可能导致转子和定子的磨损。此外，由偏心率引起的不平衡磁拉力会导致车辆振动增加并降低行驶安全性。因此，在电机设计过程中应进行偏心率分析，特别是在电动汽车应用中需考虑电气和机械因素。为此，需要一种快速且精确的方法来计算偏心电机中的磁通密度。

在 [7,8],同心式同步磁阻电机中，已采用保角映射和磁等效电路（MEC）来计算转子磁通屏障的磁阻。然后利用该结果解析确定气隙磁通密度分布和电磁转矩。在 [9],提出了一种用于表征同心式同步磁阻电机的解析方法。在 [10,11],保角映射方法已被用于永磁电机中的单边磁拉力分析 。考虑鼠笼转子的阻尼效应，文献 [12] 中提出了偏心感应电机单边磁拉力计算的解析模型。在 [13],引入了一种用于感应电机动态仿真的方法，包括混合偏心和单边磁拉力。通过有限元法计算的励磁电流被用于简化单边磁拉力模型。在 [14],对偏心圆柱转子同步电机的单边磁拉力和感应电动势进行了研究。在 [15],提出了一种数学模型，用于分析偏心率对大型立式同步电机中单边磁拉力的影响。

尽管感应电机中由偏心率引起的单边磁拉力 [16-20], 永磁同步电机 [21-25],以及凸极同步电机 [14-15],的偏心问题已被广泛研究，但关于存在偏心率的同步磁阻电机的研究文献较少。在 [26],提出了一种基于磁路法（ MEC）的解析方法，用于预测偏心同步磁阻电机的性能。然而，由于气隙定义中的近似处理，该方法不适用于偏心故障的建模与诊断。作为比较，采用了一个简化的有限元模型（FEM），未考虑定子槽和饱和效应。在 [27-28],磁动势、磁场密度以及转矩已使用磁路法（MEC）计算的同心和偏心同步磁阻电机的结果，分别。然而，这类以电流供电作为输入的模型并不适用于电机电流特征分析（MCSA）等故障诊断目的。

根据上述综述，目前仍缺乏一种快速且准确的方法来考虑具有磁通屏障的同步磁阻电机（SynRM）在动态仿真中的偏心率问题。本文旨在通过提出一种新方法来填补这一空白，该方法能够精确计算考虑转子磁通屏障、偏心率、饱和以及定子槽效应的气隙磁导函数。首次采用改进绕组函数法（MWFM）利用所计算的气隙磁导对偏心同步磁阻电机进行建模。电机电感的计算通过数值方法完成，该过程无需对匝数函数、改进绕组函数和气隙函数进行任何近似处理。采用二维时步有限元方法和实验测试来验证所提出模型的结果。本文的其他贡献如下：

• 该模型可用于初步设计 同步磁阻电机用于分析电机性能并加速设计流程。所引入的模型比有限元法显著更快，所提出模型的仿真时间仅为几秒钟，而有限元法则需要数小时。此外，所提出的模型结果与有限元法具有良好的一致性。在偏心条件下计算的径向力可用于高速区域转子的机械设计，以设计容错电机并提高电机安全性。
• 除了用于电机设计过程之外，提出的方法为分析同步磁阻电机中电机信号（如电流和转矩）在时域或频域的特性提供了一种快速仿真工具，以提取用于偏心故障诊断的有效指标。所提取的指标可用于实时驱动系统中，以检测早期阶段的偏心率。

本文的结构如下：第二节介绍了同步磁阻电机的动态模型。第三节介绍了气隙建模。第四节讨论了电感计算。第五节介绍了磁通密度、转矩和力计算。第六节讨论了模型仿真。第七节介绍了采用有限元法的电机建模。第八节描述了实验装置。第九节讨论了仿真与实验结果。最后，第十节给出了结论。

II. 同步磁阻电机的动态模型

采用多耦合电路方法来表示电压和电流关系。通过三相正弦电压激励定子绕组。 定子绕组上的电压定义为：

$$
\begin{bmatrix}
v_a \
v_b \
v_c
\end{bmatrix}
=
\begin{bmatrix}
R_s & 0 & 0 \
0 & R_s & 0 \
0 & 0 & R_s
\end{bmatrix}
\begin{bmatrix}
i_a \
i_b \
i_c
\end{bmatrix}
+
\frac{d}{dt}
\begin{bmatrix}
\psi_a \
\psi_b \
\psi_c
\end{bmatrix}
$$

其中 $v$ 是每个定子绕组的等效电阻，$i$ 是相电流，$\phi$ 是与每个定子绕组交链的磁通，其定义为：

$$
\begin{bmatrix}
\psi_a \
\psi_b \
\psi_c
\end{bmatrix}
=
\begin{bmatrix}
L_{aa} & L_{ab} & L_{ac} \
L_{ba} & L_{bb} & L_{bc} \
L_{ca} & L_{cb} & L_{cc}
\end{bmatrix}
\begin{bmatrix}
i_a \
i_b \
i_c
\end{bmatrix}
$$

任意转子角度下的电磁转矩是基于共能法并利用绕组电感计算的，如下所示：

$$
T_e(\theta_r) = \frac{1}{2} [I]^T \frac{\partial [L]}{\partial \theta_r} [I]
$$

其中 $[I]$ 是定子电流矩阵，$[L]$ 是定子电感矩阵。电机的机电方程为：

$$
T_e - T_L = J \frac{d\omega_r}{dt} + F \omega_r
$$

其中 $T_e$, $T_L$, $J$, $F$ 分别为电磁转矩和负载转矩、转子转动惯量和机械阻尼系数。转子角速度表示为：

$$
\omega_r = \frac{d\theta_r}{dt}
$$

基于上述方程中，求解同步磁阻电机的动态仿真需要进行定子电感计算。为此，必须首先建立气隙函数模型。

III. 气隙建模

为了分析偏心条件下的电机性能，需要对气隙进行精确建模。健康的同步磁阻电机的机械气隙是均匀的。然而，磁通屏障形成可变磁阻，可被视为对气隙长度的次要影响。本文首先对磁通屏障、饱和和槽对气隙函数的影响进行建模，然后改进气隙函数以考虑不同偏心度的影响。

) 同步磁阻电机的转子横截面
) 各磁通屏障的气隙长度
) 同步磁阻电机的有效气隙函数

定子槽效应对气隙的影响可按如下方式考虑：

$$
g(\varphi, \theta_r) = g_{rel}(\varphi, \theta_r) - \delta_{slot} \cos(N_s \varphi)
$$

其中 $g_{rel}$、 $\delta_{slot}$、 $N_s$、 $\varphi$ 和 $\theta_r$ 分别表示与磁通屏障相关的气隙长度、与饱和效应相关的常系数、定子槽数、定子坐标系中的角位置以及转子角位置。为了精确建模气隙函数，应估算饱和效应。饱和会降低铁芯路径的磁导率，从而增加饱和区域周围的磁阻。在[29],中已表明，可用气隙长度来代替铁芯部分磁导率的降低，以模拟铁芯中的饱和。因此，气隙长度被定义为饱和程度的函数。因此，气隙函数可表示为：

$$
g(\varphi, \theta_r, t) = g_{rel}(\varphi, \theta_r) - \delta_{slot} \cos(N_s \varphi) - \delta_{sat} \cos(2(P \omega t - \varphi))
$$

其中 $\delta_{sat}$ 与饱和效应、供电角频率和极对数有关，分别表示如下。 $\delta_{sat}$ 表达式如下 [29]:

$$
\delta_{sat} = \frac{2(k_{sat} - 1)}{3} g_0
$$

$k_{sat}$ 是未饱和与饱和条件下气隙电压基波分量之比，而 $g_0$ 是机械气隙长度。在混合偏心故障中，静态偏心和动态偏心同时发生。混合偏心情况下的气隙函数可推导如下：

$$
g(\varphi, \theta_r, t) = g_{rel}(\varphi, \theta_r) - \delta_{slot} \cos(N_s \varphi) - \delta_{sat} \cos(2(P \omega t - \varphi)) - \delta_{se} \cos(\varphi) - \delta_{de} \cos(P \omega t - \varphi)
$$

其中 $\delta_{se}$ 和 $\delta_{de}$ 分别由 (10) 和 (11) 表示。

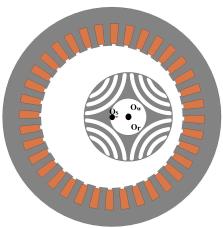
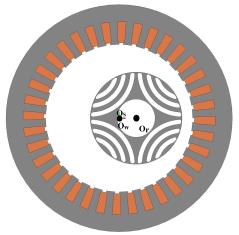
) 同步磁阻电机横截面 (a) 静态偏心
) 同步磁阻电机横截面 (b) 动态偏心

$$
\delta_{se} = \frac{|O_s - O_w|}{g_0}
$$

$$
\delta_{de} = \frac{|O_w - O_r|}{g_0}
$$

其中 $O_s$、 $O_r$ 和 $O_w$ 分别为定子、转子和旋转轴心。 图显示了不同偏心类型下定子和转子的相对位置。

IV. 同步磁阻电机电感计算

绕组函数法(WFM)基于耦合电磁方程，这些方程是通过电路理论的简单定律[30]得到的。该方法考虑了电机中所有的空间谐波。在WFM中，假设气隙具有均匀分布。在这种情况下，绕组函数定义为[30]：

$$
N(\varphi) = n(\varphi) - \langle n(\varphi) \rangle
$$

其中 $n(\varphi)$ 是定子匝数函数，表示绕组分布，而 $\langle n(\varphi) \rangle$ 是匝数函数的平均值，如下所示：

$$
\langle n(\varphi) \rangle = \frac{1}{2\pi} \int_0^{2\pi} n(\varphi) d\varphi
$$

B相电流的电感值计算如下：

$$
L_{AB}(\theta_r) = \frac{\mu_0 l r}{\pi} \int_0^{2\pi} \frac{n_A(\varphi) N_B(\varphi, \theta_r)}{g(\varphi, \theta_r)} d\varphi
$$

其中 $\mu_0$、 $r$ 和 $l$ 分别为空气磁导率、转子外半径和叠片长度。由于在电感计算中未考虑气隙变化，绕组函数法无法对凸极或偏心电机进行建模。因此，本文首次采用改进型绕组函数法对具有分布磁通屏障的同心及偏心同步磁阻电机进行建模。

在[31],中，绕组函数法（WFM）已被改进以考虑气隙偏心。线圈的改进型绕组函数法（MWFM）可表示为：

$$
M(\varphi, \theta_r) = n(\varphi) - \langle M(\theta_r) \rangle
$$

其中 $n(\varphi)$ 和 $\langle M(\theta_r) \rangle$ 是所示的改进型绕组函数的平均值：

$$
\langle M(\theta_r) \rangle = \left\langle n(\varphi) \cdot \frac{1}{g(\varphi, \theta_r)} \right\rangle \cdot \left\langle \frac{1}{g(\varphi, \theta_r)} \right\rangle^{-1}
$$

其中定义为：

$$
\left\langle \frac{1}{g(\varphi, \theta_r)} \right\rangle = \frac{1}{2\pi} \int_0^{2\pi} \frac{1}{g(\varphi, \theta_r)} d\varphi
$$

B相中的电感电流表示为：

$$
L_{AB}(\theta_r) = \frac{\mu_0 l r}{\pi} \int_0^{2\pi} n_A(\varphi) M_B(\varphi, \theta_r) g(\varphi, \theta_r)^{-1} d\varphi
$$

由于电机的特性取决于气隙磁导函数（$g^{-1}$）。由于同步磁阻电机的磁阻特性，如图1(c)所示，并结合正常与偏心状态下的气隙定义（7 和 9），气隙函数发生变化，从而导致磁导函数的变化。因此，自感和互感曲线随偏心类型和偏心度而变化。图3(a) 和 图3(b) 分别展示了健康电机以及在不同偏心度下电机定子的自感和互感。可以看出，电感值随着偏心类型和偏心度的不同而变化。此外，混合偏心（ME）会使电感曲线产生更大的畸变。

) 正常和不同偏心率情况下的定子电感（a）a相自感
) 正常和不同偏心率情况下的定子电感（b）a相和b相之间的互感

V. 磁通密度、转矩和力的计算

所提出的模型还可以计算同步磁阻电机的动态转矩。利用式(19)中定义的麦克斯韦应力张量来预测圆柱坐标系 [32]中的电磁转矩波形：

$$
\mathbf{T} = \frac{1}{\mu_0}
\begin{bmatrix}
B_r^2 - \frac{1}{2}(B_r^2 + B_\theta^2 + B_z^2) & B_r B_\theta & B_r B_z \
B_\theta B_r & B_\theta^2 - \frac{1}{2}(B_r^2 + B_\theta^2 + B_z^2) & B_\theta B_z \
B_z B_r & B_z B_\theta & B_z^2 - \frac{1}{2}(B_r^2 + B_\theta^2 + B_z^2)
\end{bmatrix}
$$

其中 $B_r$、 $B_\theta$ 和 $B_z$ 分别为磁通的径向、切向和 z 分量。电磁力定义为

$$
\mathbf{F} = \int_S \mathbf{T} \cdot \mathbf{n} \, ds
$$

其中 $S$ 是包围所考虑物体的表面，且 $\mathbf{n}$ 是垂直于表面 $S$ 的单位矢量。转子上的径向力计算为

$$
F_g(\varphi) = \frac{1}{4\mu_0} \int_0^{2\pi} B_g^2(\varphi) D \, d\varphi
$$

$F_x$ 和 $F_y$ 分量可以计算为[26]：

$$
F_x = \frac{1}{4\mu_0} \int_0^{2\pi} B_g^2(\varphi) D \cos(\varphi) \, d\varphi
$$

$$
F_y = \frac{1}{4\mu_0} \int_0^{2\pi} B_g^2(\varphi) D \sin(\varphi) \, d\varphi
$$

其中 $B_g$ 是定子内径。 由第 $i$ 个绕组在气隙中产生的磁通密度表示为 [33]：

$$
B_i(\varphi, \theta_r) = \frac{\mu_0}{g(\varphi, \theta_r)} M_i(\varphi, \theta_r) i_i
$$

其中 $i_i$ 是第 $i$ 个绕组的电流。

VI. 所提出模型的仿真

所提出的模型在 MATLAB 中使用 Intel Core i7 处理器、2.6 GHz、16 GB 内存的计算机进行仿真，仿真时长为 12 秒，时间步长为 $(1/2048)$ 秒。因此，迭代总次数为 24576。提出的方法的仿真耗时 9.54 秒完成。所提出的模型在 MATLAB 中仿真的流程图如图4所示。电机参数见表 I。

MATLAB仿真流程图

表 I ：电机参数

参数	数值
额定功率	350 W
额定转速	1500 rpm
定子极对数	2
定子槽数	36
每极磁通屏障数	3
气隙	0.45 mm
转子外径	50 毫米
叠片长度	50 毫米

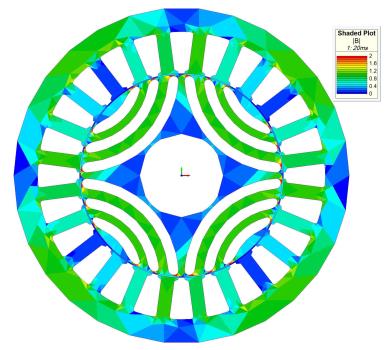
) 正常电机 (a) 的磁通密度分布
) 具有50%静态偏心的电机 (b) 的磁通密度分布

VII. 使用有限元法的电机建模

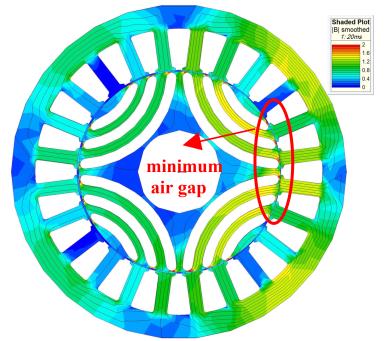
Infolytica MagNet 软件用于电机的二维有限元建模。在此模型中，考虑了电机各部分的物理复杂性以及材料的非线性特性。仿真采用瞬态运动求解器。图5显示了健康电机和具有50%静态偏心的电机的磁通密度分布。可以看出，静态偏心增加了气隙长度最小区域（电机右侧）的磁通密度。在第九节中讨论了通过有限元仿真获得的转子转矩、电机磁通密度以及径向力的 x‐y 分量，并与所提出的模型进行了比较。

VIII. 实验装置

试验台如图6所示。实验装置中使用了电压源逆变器。采用德州仪器信号处理器 TMS320F28335 以及霍尔效应电流和电压传感器用于控制系统。此外，为了滤除电流和电压信号，采用了模拟二阶低通滤波器。转矩通过将力传递给高灵敏度称重传感器来测量。一个直流发电机和一个变阻器被用来调节输出功率。文献中用于产生不同类型偏心率的各种方法已在[34]中进行了综述。本文中，为了在电机中产生偏心率，主轴承被替换为具有较大内径和较小外径的另一轴承。为了引入静态偏心，分别在转子轴与轴承之间使用同心内圈，在轴承与机壳之间使用偏心外圈。此外，为了产生动态偏心，在转子轴与轴承之间使用偏心内圈；同时，在轴承与机壳之间使用同心外圈。对于混合偏心情况，内外圈均为偏心。偏心率的值可通过加工内外圈精确确定。

实验装置

IX. 结果与讨论

所有仿真和实验测试均在额定转速和额定负载下进行。图7描绘了所提出的模型获得的50%SE下的相电流波形。图8 (a)显示了所提出的模型得到的气隙中磁通密度径向分量的分布，并与健康电机的有限元法进行了比较。为了比较，基于磁路法的引入模型[26],在图8 (a)中示出。显然，通过磁路法获得的磁通密度与实际磁通密度分布相差较大。图8 (b)显示了所提出的模型得到的气隙中磁通密度切向分量的分布，并与健康电机的有限元法进行了比较。

50%静态偏心下的相电流波形

) 提出的方法和有限元法得到的气隙磁通密度分布（a）健康电机的径向分量
) 提出的方法和有限元法得到的气隙磁通密度分布（b）健康电机的切向分量
) 提出的方法得到的健康电机及不同偏心度电机的径向分量

可以看出，本文所提出的模型结果与有限元法结果具有良好的一致性。此外，图8 (c) 展示了正常电机和具有不同偏心度的电机的气隙磁通密度径向分量的比较。通过比较图8(c)中的不同情况，可以理解到偏心率会导致气隙磁通密度的不对称分布，从而引起电机定子电流和转矩的畸变。

如第五节所示，$x - y$ 作用在转子上的径向力分量可以在正常和故障情况下通过公式(21)进行预测。图9描绘了所提出模型和有限元法计算的健康电机以及具有不同偏心度电机的径向力分量 $F_x$ 和 $F_y$ 结果。图9(a)展示了健康电机中的径向力分量 $F_x$ 和 $F_y$，在此情况下，径向力分量几乎为零。图9(b)显示了 $F_y$ 与20%SE下的 $F_x$ 相比。该力的方向指向最小气隙方向。有限元法和所提出的模型预测的力分别在220至222 N之间。在20%DE情况下，如图9 (c)所示，由于最小气隙长度随转子旋转，径向力也随之旋转。此时，有限元法和所提出的模型预测的径向力分别为216 N和220 N。图9 (d)展示了混合偏心（ME）情况（10%SE和20%DE）下的径向力分量。在此情况下，有限元法和所提出的模型预测的径向力分别为417 N和425 N。所提出的模型与有限元法结果的比较表明，在不同偏心类型下具有良好的一致性。

) 健康电机
) 具有20%静态偏心的电机
) 具有20%动态偏心的电机
) 具有10%静态偏心和20%动态偏心的电机

表II : 转子径向力的峰值

偏心类型	静态偏心率%	动态偏心率%	混合偏心率%	所提出的模型结果（N）	有限元法结果（N）
20%静态偏心	20	0	0	222	220
50%静态偏心	50	0	0	570	545
20%动态偏心	0	20	0	220	216
50%动态偏心	0	50	0	475	500
10%静态偏心和20%动态偏心	10	20	0	425	417
40%静态偏心和30%动态偏心	40	30	0	550	570

不同偏心率情况下的电流波形（experiment)

) 归一化线电流的频谱（a）健康电机
) 归一化线电流的频谱（b）具有50%静态偏心的电机

) 所提出的模型、有限元法和实验在（a）50%静态偏心中的转矩波形比较
) 所提出的模型、有限元法和实验在（b）50%动态偏心中的转矩波形比较

图10 (a) 显示了 $F_y$ 随 $F_x$ 在50%静态偏心下的变化。该力的方向指向最小气隙，其力值在有限元法和所提出的模型中分别为545 N和570 N。在50%动态偏心情况下，如图10 (b)所示，所提出模型和有限元法的力值分别为475 N和500 N。图10 (c) 展示了40%静态偏心与30%动态偏心混合偏心情况下的径向力分量。所提出模型和有限元法的力值分别为550 N和570 N。需要注意的是，在高偏心率（如50%）时，饱和效应会增强，从而影响模型的精度。然而，所提出的方法与有限元法之间仍具有良好的一致性。表II总结了不同偏心类型和偏心度下，所提出方法与有限元法得到的转子径向力峰值。可以看出，所提出的模型在 20%静态偏心和20%动态偏心情况下的精度高于98%；在 50%静态偏心和50%动态偏心情况下，精度也高于95%。

图11展示了电机在不同偏心度下的相电流实验结果。该电流可用于故障诊断。 图12演示了同步磁阻电机在正常电机和50%静态偏心情况下的归一化线电流频谱。边带分量在主频（50赫兹）附近的幅值随着偏心率的出现而升高。电机电流频谱中出现的特定频率模式可作为偏心故障诊断的指标。

图13（a）和（b）显示了所提出的方法、有限元法和实验分别对具有50%静态偏心和50%动态偏心的电机获得的电磁转矩的比较。可以看出，有限元法和实验测试结果验证了所提出模型的精度。

X. 结论

提出了一种基于改进型绕组函数法（MWFM）的数值方法，用于建模同步磁阻电机（SynRMs）中的不同类型偏心率。利用所提出的模型，计算了电机电感、气隙磁通密度、转矩以及转子上的径向力。采用麦克斯韦应力张量来预测电磁转矩。该模型可用于电动汽车应用中同步磁阻电机的初步设计。此外，还可用于同步磁阻电机的动态仿真，以获得适用于故障诊断系统（如电机电流频谱分析MCSA）的适当指标。所提出模型与有限元法（ FEM）及实验结果的比较表明，两者具有良好的一致性。需要指出的是，所计算的径向力通过所提出的模型略高于有限元法，尤其是在严重的偏心情况下。然而，在同步磁阻电机设计流程中，将其视为一个安全系数是有用的。此外，仿真的时间为几秒钟，而有限元法需要数小时。因此，提出的方法结果适用于电机设计和故障诊断系统。