给定一个整数数组 nums 和一个目标值 target,请你在该数组中找出和为目标值的那 两个 整数,并返回他们的数组下标。
你可以假设每种输入只会对应一个答案。但是,你不能重复利用这个数组中同样的元素。
示例:
给定 nums = [2, 7, 11, 15], target = 9
因为 nums[0] + nums[1] = 2 + 7 = 9
所以返回 [0, 1]官方题解
方法一:暴力法
暴力法很简单,遍历每个元素 xx,并查找是否存在一个值与 target - xtarget−x 相等的目标元素。
- Java
public int[] twoSum(int[] nums, int target) {
for (int i = 0; i < nums.length; i++) {
for (int j = i + 1; j < nums.length; j++) {
if (nums[j] == target - nums[i]) {
return new int[] { i, j };
}
}
}
throw new IllegalArgumentException("No two sum solution");
}
复杂度分析:
-
时间复杂度:O(n^2)O(n2), 对于每个元素,我们试图通过遍历数组的其余部分来寻找它所对应的目标元素,这将耗费 O(n)O(n) 的时间。因此时间复杂度为 O(n^2)O(n2)。
-
空间复杂度:O(1)O(1)。
方法二:两遍哈希表
为了对运行时间复杂度进行优化,我们需要一种更有效的方法来检查数组中是否存在目标元素。如果存在,我们需要找出它的索引。保持数组中的每个元素与其索引相互对应的最好方法是什么?哈希表。
通过以空间换取速度的方式,我们可以将查找时间从 O(n)O(n) 降低到 O(1)O(1)。哈希表正是为此目的而构建的,它支持以 近似 恒定的时间进行快速查找。我用“近似”来描述,是因为一旦出现冲突,查找用时可能会退化到 O(n)O(n)。但只要你仔细地挑选哈希函数,在哈希表中进行查找的用时应当被摊销为 O(1)O(1)。
一个简单的实现使用了两次迭代。在第一次迭代中,我们将每个元素的值和它的索引添加到表中。然后,在第二次迭代中,我们将检查每个元素所对应的目标元素(target - nums[i]target−nums[i])是否存在于表中。注意,该目标元素不能是 nums[i]nums[i] 本身!
- Java
public int[] twoSum(int[] nums, int target) {
Map<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < nums.length; i++) {
map.put(nums[i], i);
}
for (int i = 0; i < nums.length; i++) {
int complement = target - nums[i];
if (map.containsKey(complement) && map.get(complement) != i) {
return new int[] { i, map.get(complement) };
}
}
throw new IllegalArgumentException("No two sum solution");
}
复杂度分析:
-
时间复杂度:O(n)O(n), 我们把包含有 nn 个元素的列表遍历两次。由于哈希表将查找时间缩短到 O(1)O(1) ,所以时间复杂度为 O(n)O(n)。
-
空间复杂度:O(n)O(n), 所需的额外空间取决于哈希表中存储的元素数量,该表中存储了 nn 个元素。
方法三:一遍哈希表
事实证明,我们可以一次完成。在进行迭代并将元素插入到表中的同时,我们还会回过头来检查表中是否已经存在当前元素所对应的目标元素。如果它存在,那我们已经找到了对应解,并立即将其返回。
- Java
public int[] twoSum(int[] nums, int target) {
Map<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < nums.length; i++) {
int complement = target - nums[i];
if (map.containsKey(complement)) {
return new int[] { map.get(complement), i };
}
map.put(nums[i], i);
}
throw new IllegalArgumentException("No two sum solution");
}
复杂度分析:
-
时间复杂度:O(n)O(n), 我们只遍历了包含有 nn 个元素的列表一次。在表中进行的每次查找只花费 O(1)O(1) 的时间。
-
空间复杂度:O(n)O(n), 所需的额外空间取决于哈希表中存储的元素数量,该表最多需要存储 nn 个元素。
给出两个 非空 的链表用来表示两个非负的整数。其中,它们各自的位数是按照 逆序 的方式存储的,并且它们的每个节点只能存储 一位 数字。
如果,我们将这两个数相加起来,则会返回一个新的链表来表示它们的和。
您可以假设除了数字 0 之外,这两个数都不会以 0 开头。
示例:
输入:(2 -> 4 -> 3) + (5 -> 6 -> 4)
输出:7 -> 0 -> 8
原因:342 + 465 = 807/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
if(l1 == null)
return l2;
if(l2 == null)
return l1;
ListNode head = new ListNode(0);
ListNode current = head;
int carry = 0;
while(l1 != null || l2 != null) {
int x = (l1 != null) ? l1.val : 0;
int y = (l2 != null) ? l2.val : 0;
int sum = x + y + carry;
carry = sum / 10;
current.next = new ListNode(sum % 10);
current = current.next;
if(l1 != null)
l1 = l1.next;
if(l2 != null)
l2 = l2.next;
}
if(carry > 0)
current.next = new ListNode(carry);
return head.next;
}
}给定一个字符串,请你找出其中不含有重复字符的 最长子串 的长度。
示例 1:
输入: "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
示例 2:
输入: "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。
示例 3:
输入: "pwwkew" 输出: 3 解释: 因为无重复字符的最长子串是"wke",所以其长度为 3。 请注意,你的答案必须是 子串 的长度,"pwke"是一个子序列,不是子串。
方法一:暴力法
思路
逐个检查所有的子字符串,看它是否不含有重复的字符。
算法
假设我们有一个函数 boolean allUnique(String substring) ,如果子字符串中的字符都是唯一的,它会返回 true,否则会返回 false。 我们可以遍历给定字符串 s 的所有可能的子字符串并调用函数 allUnique。 如果事实证明返回值为 true,那么我们将会更新无重复字符子串的最大长度的答案。
现在让我们填补缺少的部分:
-
为了枚举给定字符串的所有子字符串,我们需要枚举它们开始和结束的索引。假设开始和结束的索引分别为 ii和 jj。那么我们有 0 \leq i \lt j \leq n0≤i<j≤n(这里的结束索引 jj 是按惯例排除的)。因此,使用 ii 从 0 到 n - 1n−1 以及 jj 从 i+1i+1 到 nn 这两个嵌套的循环,我们可以枚举出
s的所有子字符串。 -
要检查一个字符串是否有重复字符,我们可以使用集合。我们遍历字符串中的所有字符,并将它们逐个放入
set中。在放置一个字符之前,我们检查该集合是否已经包含它。如果包含,我们会返回false。循环结束后,我们返回true。
- Java
public class Solution {
public int lengthOfLongestSubstring(String s) {
int n = s.length();
int ans = 0;
for (int i = 0; i < n; i++)
for (int j = i + 1; j <= n; j++)
if (allUnique(s, i, j)) ans = Math.max(ans, j - i);
return ans;
}
public boolean allUnique(String s, int start, int end) {
Set<Character> set = new HashSet<>();
for (int i = start; i < end; i++) {
Character ch = s.charAt(i);
if (set.contains(ch)) return false;
set.add(ch);
}
return true;
}
}
复杂度分析
-
时间复杂度:O(n^3)O(n3) 。
要验证索引范围在 [i, j)[i,j) 内的字符是否都是唯一的,我们需要检查该范围中的所有字符。 因此,它将花费 O(j - i)O(j−i) 的时间。
对于给定的
i,对于所有 j \in [i+1, n]j∈[i+1,n] 所耗费的时间总和为:\sum_{i+1}^{n}O(j - i)i+1∑nO(j−i)
因此,执行所有步骤耗去的时间总和为:
O\left(\sum_{i = 0}^{n - 1}\left(\sum_{j = i + 1}^{n}(j - i)\right)\right) = O\left(\sum_{i = 0}^{n - 1}\frac{(1 + n - i)(n - i)}{2}\right) = O(n^3)O(i=0∑n−1(j=i+1∑n(j−i)))=O(i=0∑n−12(1+n−i)(n−i))=O(n3)
-
空间复杂度:O(min(n, m))O(min(n,m)),我们需要 O(k)O(k) 的空间来检查子字符串中是否有重复字符,其中 kk 表示
Set的大小。而 Set 的大小取决于字符串 nn 的大小以及字符集/字母 mm 的大小。
方法二:滑动窗口
算法
暴力法非常简单,但它太慢了。那么我们该如何优化它呢?
在暴力法中,我们会反复检查一个子字符串是否含有有重复的字符,但这是没有必要的。如果从索引 ii 到 j - 1j−1之间的子字符串 s_{ij}sij 已经被检查为没有重复字符。我们只需要检查 s[j]s[j] 对应的字符是否已经存在于子字符串 s_{ij}sij中。
要检查一个字符是否已经在子字符串中,我们可以检查整个子字符串,这将产生一个复杂度为 O(n^2)O(n2) 的算法,但我们可以做得更好。
通过使用 HashSet 作为滑动窗口,我们可以用 O(1)O(1) 的时间来完成对字符是否在当前的子字符串中的检查。
滑动窗口是数组/字符串问题中常用的抽象概念。 窗口通常是在数组/字符串中由开始和结束索引定义的一系列元素的集合,即 [i, j)[i,j)(左闭,右开)。而滑动窗口是可以将两个边界向某一方向“滑动”的窗口。例如,我们将 [i, j)[i,j)向右滑动 11 个元素,则它将变为 [i+1, j+1)[i+1,j+1)(左闭,右开)。
回到我们的问题,我们使用 HashSet 将字符存储在当前窗口 [i, j)[i,j)(最初 j = ij=i)中。 然后我们向右侧滑动索引 jj,如果它不在 HashSet 中,我们会继续滑动 jj。直到 s[j] 已经存在于 HashSet 中。此时,我们找到的没有重复字符的最长子字符串将会以索引 ii 开头。如果我们对所有的 ii 这样做,就可以得到答案。
- Java
public class Solution {
public int lengthOfLongestSubstring(String s) {
int n = s.length();
Set<Character> set = new HashSet<>();
int ans = 0, i = 0, j = 0;
while (i < n && j < n) {
// try to extend the range [i, j]
if (!set.contains(s.charAt(j))){
set.add(s.charAt(j++));
ans = Math.max(ans, j - i);
}
else {
set.remove(s.charAt(i++));
}
}
return ans;
}
}
复杂度分析
-
时间复杂度:O(2n) = O(n)O(2n)=O(n),在最糟糕的情况下,每个字符将被 ii 和 jj 访问两次。
-
空间复杂度:O(min(m, n))O(min(m,n)),与之前的方法相同。滑动窗口法需要 O(k)O(k) 的空间,其中 kk 表示
Set的大小。而 Set 的大小取决于字符串 nn 的大小以及字符集 / 字母 mm 的大小。
方法三:优化的滑动窗口
上述的方法最多需要执行 2n 个步骤。事实上,它可以被进一步优化为仅需要 n 个步骤。我们可以定义字符到索引的映射,而不是使用集合来判断一个字符是否存在。 当我们找到重复的字符时,我们可以立即跳过该窗口。
也就是说,如果 s[j]s[j] 在 [i, j)[i,j) 范围内有与 j'j′ 重复的字符,我们不需要逐渐增加 ii 。 我们可以直接跳过 [i,j'][i,j′] 范围内的所有元素,并将 ii 变为 j' + 1j′+1。
Java(使用 HashMap)
- Java
public class Solution {
public int lengthOfLongestSubstring(String s) {
int n = s.length(), ans = 0;
Map<Character, Integer> map = new HashMap<>(); // current index of character
// try to extend the range [i, j]
for (int j = 0, i = 0; j < n; j++) {
if (map.containsKey(s.charAt(j))) {
i = Math.max(map.get(s.charAt(j)), i);
}
ans = Math.max(ans, j - i + 1);
map.put(s.charAt(j), j + 1);
}
return ans;
}
}
Java(假设字符集为 ASCII 128)
以前的我们都没有对字符串 s 所使用的字符集进行假设。
当我们知道该字符集比较小的时侯,我们可以用一个整数数组作为直接访问表来替换 Map。
常用的表如下所示:
int [26]用于字母 ‘a’ - ‘z’ 或 ‘A’ - ‘Z’int [128]用于ASCII码int [256]用于扩展ASCII码
- Java
public class Solution {
public int lengthOfLongestSubstring(String s) {
int n = s.length(), ans = 0;
int[] index = new int[128]; // current index of character
// try to extend the range [i, j]
for (int j = 0, i = 0; j < n; j++) {
i = Math.max(index[s.charAt(j)], i);
ans = Math.max(ans, j - i + 1);
index[s.charAt(j)] = j + 1;
}
return ans;
}
}
复杂度分析
-
时间复杂度:O(n)O(n),索引 jj 将会迭代 nn 次。
-
空间复杂度(HashMap):O(min(m, n))O(min(m,n)),与之前的方法相同。
-
空间复杂度(Table):O(m)O(m),mm 是字符集的大小。
给定一个字符串 s,找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。
示例 1:
输入: "babad"
输出: "bab"
注意: "aba" 也是一个有效答案。
示例 2:
输入: "cbbd"
输出: "bb"摘要
这篇文章是为中级读者而写的。它介绍了回文,动态规划以及字符串处理。请确保你理解什么是回文。回文是一个正读和反读都相同的字符串,例如,\textrm{“aba”}“aba” 是回文,而 \textrm{“abc”}“abc” 不是。
解决方案
方法一:暴力法
很明显,暴力法将选出所有子字符串可能的开始和结束位置,并检验它是不是回文。
class Solution {
public String longestPalindrome(String s) {
if(s == null || s.length() < 1)
return "";
if(s.length() == 1)
return s;
int start=0, maxlength=1;//记录最大回文子串的起始位置以及长度
for(int i = 0; i < s.length(); i++)
for(int j = i + 1; j < s.length(); j++) {//从当前位置的下一个开始算
int temp1, temp2;
for(temp1 = i, temp2 = j; temp1 < temp2; temp1++, temp2--) {
if(s.charAt(temp1) != s.charAt(temp2))
break;
}
if(temp1 >= temp2 && j - i + 1 > maxlength) {//这里要注意条件为temp1>=temp2,因为如果是偶数个字符,相邻的两个经上一步会出现大于的情况
maxlength = j - i + 1;
start = i;
}
}
return s.substring(start, start + maxlength);//利用string中的substr函数来返回相应的子串,第一个参数是起始位置,第二个参数是字符个数
}
}复杂度分析
-
时间复杂度:O(n^3)O(n3),假设 nn 是输入字符串的长度,则 \binom{n}{2} = \frac{n(n-1)}{2}(2n)=2n(n−1) 为此类子字符串(不包括字符本身是回文的一般解法)的总数。因为验证每个子字符串需要 O(n)O(n) 的时间,所以运行时间复杂度是 O(n^3)O(n3)。
-
空间复杂度:O(1)O(1)。
方法二:动态规划
为了改进暴力法,我们首先观察如何避免在验证回文时进行不必要的重复计算。考虑 \textrm{“ababa”}“ababa” 这个示例。如果我们已经知道 \textrm{“bab”}“bab” 是回文,那么很明显,\textrm{“ababa”}“ababa” 一定是回文,因为它的左首字母和右尾字母是相同的。
我们给出 P(i,j)P(i,j) 的定义如下:
P(i,j) = \begin{cases} \text{true,} &\quad\text{如果子串} S_i \dots S_j \text{是回文子串}\\ \text{false,} &\quad\text{其它情况} \end{cases}P(i,j)={true,false,如果子串Si…Sj是回文子串其它情况
因此,
P(i, j) = ( P(i+1, j-1) \text{ and } S_i == S_j )P(i,j)=(P(i+1,j−1) and Si==Sj)
基本示例如下:
P(i, i) = trueP(i,i)=true
P(i, i+1) = ( S_i == S_{i+1} )P(i,i+1)=(Si==Si+1)
这产生了一个直观的动态规划解法,我们首先初始化一字母和二字母的回文,然后找到所有三字母回文,并依此类推…
复杂度分析
-
时间复杂度:O(n^2)O(n2),这里给出我们的运行时间复杂度为 O(n^2)O(n2) 。
-
空间复杂度:O(n^2)O(n2),该方法使用 O(n^2)O(n2) 的空间来存储表。
class Solution {
public String longestPalindrome(String s) {
if(s == null || s.length() < 1)
return "";
int[][] array = new int[s.length()][s.length()];
int start = 0;
int length = 1;
for(int i = 0; i < s.length(); i++) {
array[i][i] = 1;
if(i + 1 < s.length() && s.charAt(i) == s.charAt(i + 1)) {
array[i][i + 1] = 1;
start = i;
length = 2;
}
}
for(int l = 3; l <= s.length(); l++) {//子串长度
for(int i = 0; i + l - 1 < s.length(); i++) {//枚举子串的起始点
int e = i + l - 1;
if(s.charAt(i) == s.charAt(e) && array[i + 1][e - 1] == 1) {
array[i][e] = 1;
start = i;
length = l;
}
}
}
return s.substring(start, start + length);
}
}补充练习
你能进一步优化上述解法的空间复杂度吗?
方法三:中心扩展算法
事实上,只需使用恒定的空间,我们就可以在 O(n^2)O(n2) 的时间内解决这个问题。
我们观察到回文中心的两侧互为镜像。因此,回文可以从它的中心展开,并且只有 2n - 12n−1 个这样的中心。
你可能会问,为什么会是 2n - 12n−1 个,而不是 nn 个中心?原因在于所含字母数为偶数的回文的中心可以处于两字母之间(例如 \textrm{“abba”}“abba” 的中心在两个 \textrm{‘b’}‘b’ 之间)。
- Java
public String longestPalindrome(String s) {
if (s == null || s.length() < 1) return "";
int start = 0, end = 0;
for (int i = 0; i < s.length(); i++) {
int len1 = expandAroundCenter(s, i, i);
int len2 = expandAroundCenter(s, i, i + 1);
int len = Math.max(len1, len2);
if (len > end - start) {
start = i - (len - 1) / 2;
end = i + len / 2;
}
}
return s.substring(start, end + 1);
}
private int expandAroundCenter(String s, int left, int right) {
int L = left, R = right;
while (L >= 0 && R < s.length() && s.charAt(L) == s.charAt(R)) {
L--;
R++;
}
return R - L - 1;
}
复杂度分析
-
时间复杂度:O(n^2)O(n2),由于围绕中心来扩展回文会耗去 O(n)O(n) 的时间,所以总的复杂度为 O(n^2)O(n2)。
-
空间复杂度:O(1)O(1)。
给定 n 个非负整数 a1,a2,...,an,每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
说明:你不能倾斜容器,且 n 的值至少为 2。

图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例:
输入: [1,8,6,2,5,4,8,3,7]
输出: 49摘要
如题意,垂直的两条线段将会与坐标轴构成一个矩形区域,较短线段的长度将会作为矩形区域的宽度,两线间距将会作为矩形区域的长度,而我们必须最大化该矩形区域的面积。
解决方案
方法一:暴力法
算法
在这种情况下,我们将简单地考虑每对可能出现的线段组合并找出这些情况之下的最大面积。
- Java
public class Solution {
public int maxArea(int[] height) {
int maxarea = 0;
for (int i = 0; i < height.length; i++)
for (int j = i + 1; j < height.length; j++)
maxarea = Math.max(maxarea, Math.min(height[i], height[j]) * (j - i));
return maxarea;
}
}
复杂度分析
- 时间复杂度:O(n^2)O(n2),计算所有 \frac{n(n-1)}{2}2n(n−1) 种高度组合的面积。
- 空间复杂度:O(1)O(1),使用恒定的额外空间。
方法二:双指针法
算法
这种方法背后的思路在于,两线段之间形成的区域总是会受到其中较短那条长度的限制。此外,两线段距离越远,得到的面积就越大。
我们在由线段长度构成的数组中使用两个指针,一个放在开始,一个置于末尾。 此外,我们会使用变量 maxareamaxarea 来持续存储到目前为止所获得的最大面积。 在每一步中,我们会找出指针所指向的两条线段形成的区域,更新 maxareamaxarea,并将指向较短线段的指针向较长线段那端移动一步。
这种方法如何工作?
最初我们考虑由最外围两条线段构成的区域。现在,为了使面积最大化,我们需要考虑更长的两条线段之间的区域。如果我们试图将指向较长线段的指针向内侧移动,矩形区域的面积将受限于较短的线段而不会获得任何增加。但是,在同样的条件下,移动指向较短线段的指针尽管造成了矩形宽度的减小,但却可能会有助于面积的增大。因为移动较短线段的指针会得到一条相对较长的线段,这可以克服由宽度减小而引起的面积减小。
- Java
public class Solution {
public int maxArea(int[] height) {
int maxarea = 0, l = 0, r = height.length - 1;
while (l < r) {
maxarea = Math.max(maxarea, Math.min(height[l], height[r]) * (r - l));
if (height[l] < height[r])
l++;
else
r--;
}
return maxarea;
}
}
复杂度分析
-
时间复杂度:O(n)O(n),一次扫描。
-
空间复杂度:O(1)O(1),使用恒定的空间。
给定一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?找出所有满足条件且不重复的三元组。
注意:答案中不可以包含重复的三元组。
例如, 给定数组 nums = [-1, 0, 1, 2, -1, -4],
满足要求的三元组集合为:
[
[-1, 0, 1],
[-1, -1, 2]
]class Solution {
public List<List<Integer>> threeSum(int[] nums) {
List<List<Integer>> res = new ArrayList();
Arrays.sort(nums);
for(int k=0;k<nums.length - 2;k++){
int i = k+1,j = nums.length - 1;//***
while(i < j){
int value = nums[i] + nums[j];
if(value == (-nums[k])){
List<Integer> list = new ArrayList();
list.add(nums[k]);
list.add(nums[i]);
list.add(nums[j]);
res.add(list);
//重值处理
//****一定要有i < j条件,否则i会到最后
while(i<j && nums[i] == nums[i+1]){
i++;
}
//****一定要有i < j条件,否则j会取-1
while(i<j && nums[j] == nums[j-1]){
j--;
}
//***
i++;
j--;
}
else if(value < (-nums[k]))
i++;
else
j--;
}
//****重值处理
while(k < nums.length-3 && nums[k] == nums[k+1]){
k++;
}
}
return res;
}
}给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。

示例:
输入:"23"
输出:["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].class Solution {
Map<String, String> map = new HashMap<String, String>();
List<String> result = new ArrayList<String>();
//深度优先遍历
private void digui(String currStr, String digits) {
if(digits.length() == 0) {
result.add(currStr);
return;
}
String digit = digits.substring(0, 1);
String str = map.get(digit);
for(int i = 0; i < str.length(); i++) {
digui(currStr + str.charAt(i), digits.substring(1));
}
}
public List<String> letterCombinations(String digits) {
map.put("2", "abc");
map.put("3", "def");
map.put("4", "ghi");
map.put("5", "jkl");
map.put("6", "mno");
map.put("7", "pqrs");
map.put("8", "tuv");
map.put("9", "wxyz");
if(digits.length() != 0)
digui("", digits);
return result;
}
}给定一个链表,删除链表的倒数第 n 个节点,并且返回链表的头结点。
示例:
给定一个链表: 1->2->3->4->5, 和 n = 2.
当删除了倒数第二个节点后,链表变为 1->2->3->5.
说明:
给定的 n 保证是有效的。
进阶:
你能尝试使用一趟扫描实现吗?
摘要
本文适用于初学者。它介绍了以下内容:链表的遍历和删除其末尾的第 n 个元素。
解决方案
方法一:两次遍历算法
思路
我们注意到这个问题可以容易地简化成另一个问题:删除从列表开头数起的第 (L - n + 1)(L−n+1) 个结点,其中 LL 是列表的长度。只要我们找到列表的长度 LL,这个问题就很容易解决。
算法
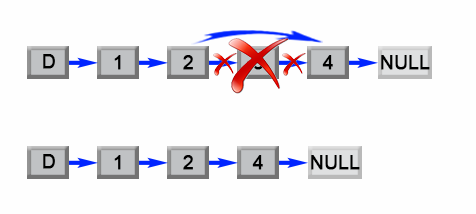
首先我们将添加一个哑结点作为辅助,该结点位于列表头部。哑结点用来简化某些极端情况,例如列表中只含有一个结点,或需要删除列表的头部。在第一次遍历中,我们找出列表的长度 LL。然后设置一个指向哑结点的指针,并移动它遍历列表,直至它到达第 (L - n)(L−n)个结点那里。我们把第 (L - n)(L−n) 个结点的 next 指针重新链接至第 (L - n + 2)(L−n+2) 个结点,完成这个算法。
图 1. 删除列表中的第 L - n + 1 个元素
- Java
public ListNode removeNthFromEnd(ListNode head, int n) {
ListNode dummy = new ListNode(0);
dummy.next = head;
int length = 0;
ListNode first = head;
while (first != null) {
length++;
first = first.next;
}
length -= n;
first = dummy;
while (length > 0) {
length--;
first = first.next;
}
first.next = first.next.next;
return dummy.next;
}
复杂度分析
-
时间复杂度:O(L)O(L),该算法对列表进行了两次遍历,首先计算了列表的长度 LL 其次找到第 (L - n)(L−n) 个结点。 操作执行了 2L-n2L−n 步,时间复杂度为 O(L)O(L)。
-
空间复杂度:O(1)O(1),我们只用了常量级的额外空间。
方法二:一次遍历算法
算法
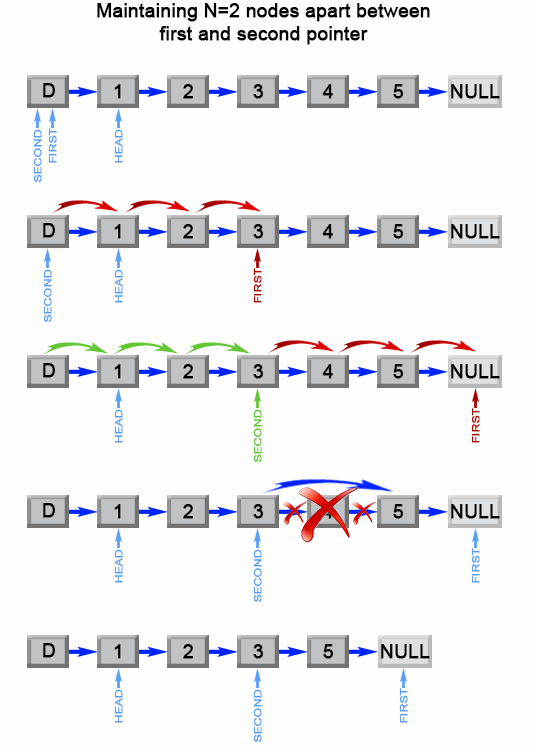
上述算法可以优化为只使用一次遍历。我们可以使用两个指针而不是一个指针。第一个指针从列表的开头向前移动 n+1n+1 步,而第二个指针将从列表的开头出发。现在,这两个指针被 nn 个结点分开。我们通过同时移动两个指针向前来保持这个恒定的间隔,直到第一个指针到达最后一个结点。此时第二个指针将指向从最后一个结点数起的第 nn 个结点。我们重新链接第二个指针所引用的结点的 next 指针指向该结点的下下个结点。
图 2. 删除链表的倒数第 N 个元素
- Java
public ListNode removeNthFromEnd(ListNode head, int n) {
ListNode dummy = new ListNode(0);
dummy.next = head;
ListNode first = dummy;
ListNode second = dummy;
// Advances first pointer so that the gap between first and second is n nodes apart
for (int i = 1; i <= n + 1; i++) {
first = first.next;
}
// Move first to the end, maintaining the gap
while (first != null) {
first = first.next;
second = second.next;
}
second.next = second.next.next;
return dummy.next;
}
复杂度分析
-
时间复杂度:O(L)O(L),该算法对含有 LL 个结点的列表进行了一次遍历。因此时间复杂度为 O(L)O(L)。
-
空间复杂度:O(1)O(1),我们只用了常量级的额外空间。
给定一个只包括 '(',')','{','}','[',']' 的字符串,判断字符串是否有效。
有效字符串需满足:
- 左括号必须用相同类型的右括号闭合。
- 左括号必须以正确的顺序闭合。
注意空字符串可被认为是有效字符串。
示例 1:
输入: "()"
输出: true
示例 2:
输入: "()[]{}"
输出: true
示例 3:
输入: "(]"
输出: false
示例 4:
输入: "([)]"
输出: false
示例 5:
输入: "{[]}"
输出: trueclass Solution {
public boolean isValid(String s) {
Stack<Character> stack = new Stack();
for(int i = 0; i < s.length(); i++) {
switch(s.charAt(i)) {
case '(' : stack.push(s.charAt(i)); break;
case '{' : stack.push(s.charAt(i)); break;
case '[' : stack.push(s.charAt(i)); break;
case ')' : if(stack.empty() || stack.pop() != '(') return false; break;
case '}' : if(stack.empty() || stack.pop() != '{') return false; break;
case ']' : if(stack.empty() || stack.pop() != '[') return false; break;
}
}
return stack.empty();
}
}




 本文精选LeetCode上的经典算法题目,深入解析两数之和、两数相加、无重复字符最长子串、最长回文子串、盛水容器等题目的多种解法,涵盖暴力法、哈希表、滑动窗口、动态规划、中心扩展算法等策略,旨在提升算法理解和编程技巧。
本文精选LeetCode上的经典算法题目,深入解析两数之和、两数相加、无重复字符最长子串、最长回文子串、盛水容器等题目的多种解法,涵盖暴力法、哈希表、滑动窗口、动态规划、中心扩展算法等策略,旨在提升算法理解和编程技巧。
















 4151
4151

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








