codeforces1151E Number of Components（思维）

最新推荐文章于 2025-02-17 19:23:41 发布

原创最新推荐文章于 2025-02-17 19:23:41 发布 · 459 阅读

1 ·

CC 4.0 BY-SA版权

思维专栏收录该内容

8 篇文章

订阅专栏

博客围绕n个节点的链展开，相邻节点有路且各节点有权值，需计算权值在【l,r】的点的连通块数量。思路是求每个节点作为连通块最右边节点的次数，根据相关条件推出代码，对于a[n]，将a[n+1]赋值为n+1。

题意：n个节点的链，相邻节点有路，每个点一个权值，f（l，r）为权值在【l,r】的点的连通块数量求
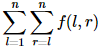
在这里插入图片描述
思路：求每个节点作为连通块的最右边的节点的次数，区间【l,r】有连通块的最右边为a[i]则要满足条件,a[i]能满足区间[l,r]，a[i+1]不能满足区间[l,r]；
就可以推出以下代码了；

    for(int i = 1; i <= n; i++)
    {
        if(a[i] > a[i + 1]) ans += (a[i] - a[i + 1]) * (n - a[i] + 1);
        if(a[i] < a[i + 1]) ans += a[i] * (a[i + 1] - a[i]);
    }

对于a[n]，只需要把a[n+1]赋值为n+1即可
代码：

#include <bits/stdc++.h>
using namespace std;

#define ll long long
const int maxn = 1e5 + 5;

ll a[maxn];

int main()
{
//    freopen("in.txt", "r", stdin);
    int n; cin >> n;
    for(int i = 1; i <= n; i++) cin >> a[i];
    a[n + 1] = n + 1;
    ll ans = 0;
    for(int i = 1; i <= n; i++)
    {
        if(a[i] > a[i + 1]) ans += (a[i] - a[i + 1]) * (n - a[i] + 1);
        if(a[i] < a[i + 1]) ans += a[i] * (a[i + 1] - a[i]);
    }
    cout << ans << '\n';
    return 0;
}