路网的存储结构
使用邻接矩阵存储路网的最大优点在于它容易确定某一给定节点射入和发出的弧的集合。如对于节点vi来说,邻接矩阵第i行中的每一个”1”就相当于从节点vi发出一条弧,而第i列中的每个1就相当于有一条弧射入节点vi.
邻接表是另一种常用的图的存储结构。常用于稀疏图。它为稀疏图G的每一个节点分配一个链表,共计m个链表。节点vi∈V对应的链表包含的元素是邻接于节点vi的节点集。
路网作为大型稀疏网络,具有交叉口转向限制,因此普通的邻接表存储结构不能满足,需要针对路网的特点以及导航中路线优化的要求,寻求合适的存储结构存储路网,达到存储量尽可能小,同时便于路线优化算法对其进行操作,还能够正确表达交叉口转向限制,合理存储节点权重等要求。
当前最常用的路网存储结构是一种称为“前向关联边”的链表结构。其核心是在于将同一个节点发出的所有弧存放在一起。首先分配一个长度为n的数组,该数组每一个元素对应一个节点,每个节点中有一个指针LinkEdgesPointer,记录由此节点发出的第一条弧在整个弧集中的起始位置,此外,还用一个长度为m的数组LinkEdges存储LinkEdgePointer指针所指向的弧
这种存储结构的一个明显好处是节省存储空间。仅仅使用一个长度为n的数组和一个长度为m的数组,而通常的存储结构需要两个长度为m的数组(一般n<<m).此外,该结构还可方便地对某一给定的节点发出的所有弧进行操作。
更重要的是,该存储结构拥有一个其他存储结构所不具备的特性,即在表示路网的同时,还暗含了交叉口行为,换句话说,车辆在临近给定交叉口时允许采取的操作,如直行,左转、右转等也通过该存储结构隐含的表达出来,具体说,当车辆由弧(i,j)即将到达节点j时,他下一步可采取的操作(下一个可能到达的节点)可以在LinkedEdges数组中找到,其在LinkedEdges数组中的起始位置由该节点的LinkEdgesPointer给出。例如图1-9所示的交叉路口,可以用如图1-10所示的结构图来表示。
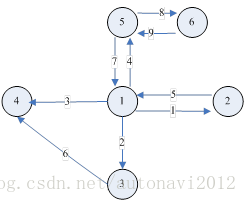
图1-9 交叉路口
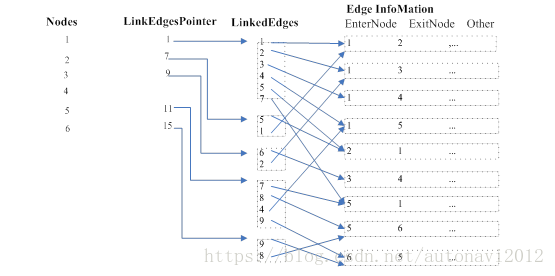
图1-10 没有禁则关系的交叉路口的表达方法
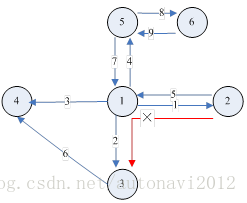
考虑转向限制,有的交叉路口是禁止左转的,如下图1-11。这种情况下,上面的前向关联边就无法表达这种关系,因此还需要对上面的结构加以改造。
图的两种基本存储结构:邻接矩阵和邻接表,下面分别介绍。
1.1 邻接矩阵
设有一个具有n个节点的有向图G=(V,E),V=(v1,v2…vn).最简单的图的存储结构是一个n×n的0-1阶矩阵A=(aij)n*n来定义,其中:

使用邻接矩阵存储路网的最大优点在于它容易确定某一给定节点射入和发出的弧的集合。如对于节点vi来说,邻接矩阵第i行中的每一个”1”就相当于从节点vi发出一条弧,而第i列中的每个1就相当于有一条弧射入节点vi.
由于邻接矩阵有n的平方个元素,故采用邻接矩阵存储路网的空间代价是O(n3),而与弧的实际数量无关。由于实际路网是一个大型的稀疏图,数据的冗余很大,不适宜采用。
邻接表是另一种常用的图的存储结构。常用于稀疏图。它为稀疏图G的每一个节点分配一个链表,共计m个链表。节点vi∈V对应的链表包含的元素是邻接于节点vi的节点集。
根据定义,稀疏图有m=O(n)条边,因此,用一个邻接表描述稀疏图只需要O(n)个存储空间,显然优于邻接矩阵。我们使用改造的邻接表来表达路网。
路网作为大型稀疏网络,具有交叉口转向限制,因此普通的邻接表存储结构不能满足,需要针对路网的特点以及导航中路线优化的要求,寻求合适的存储结构存储路网,达到存储量尽可能小,同时便于路线优化算法对其进行操作,还能够正确表达交叉口转向限制,合理存储节点权重等要求。
当前最常用的路网存储结构是一种称为“前向关联边”的链表结构。其核心是在于将同一个节点发出的所有弧存放在一起。首先分配一个长度为n的数组,该数组每一个元素对应一个节点,每个节点中有一个指针LinkEdgesPointer,记录由此节点发出的第一条弧在整个弧集中的起始位置,此外,还用一个长度为m的数组LinkEdges存储LinkEdgePointer指针所指向的弧
这种存储结构的一个明显好处是节省存储空间。仅仅使用一个长度为n的数组和一个长度为m的数组,而通常的存储结构需要两个长度为m的数组(一般n<<m).此外,该结构还可方便地对某一给定的节点发出的所有弧进行操作。
更重要的是,该存储结构拥有一个其他存储结构所不具备的特性,即在表示路网的同时,还暗含了交叉口行为,换句话说,车辆在临近给定交叉口时允许采取的操作,如直行,左转、右转等也通过该存储结构隐含的表达出来,具体说,当车辆由弧(i,j)即将到达节点j时,他下一步可采取的操作(下一个可能到达的节点)可以在LinkedEdges数组中找到,其在LinkedEdges数组中的起始位置由该节点的LinkEdgesPointer给出。例如图1-9所示的交叉路口,可以用如图1-10所示的结构图来表示。

图1-9 交叉路口

图1-10 没有禁则关系的交叉路口的表达方法
考虑转向限制,有的交叉路口是禁止左转的,如下图1-11。这种情况下,上面的前向关联边就无法表达这种关系,因此还需要对上面的结构加以改造。

图1-11 有禁行关系的交叉路口
可以在每个节点中添加一个标志信息,该标示信息提示在该节点处有没有转向





 本文介绍了图的两种基本存储结构——邻接矩阵和邻接表在路网导航路径规划中的应用。邻接矩阵虽然直观但空间效率低,不适合表示稀疏图。邻接表则更适用于存储大型稀疏图,如实际的路网,可以有效减少存储空间。在邻接表基础上,通过添加节点标志信息来处理转向限制,提高路径规划的准确性。文章还讨论了Edge结构体的设计,分为路径规划所需信息和额外模块所需信息两部分,以优化内存管理和规划速度。
本文介绍了图的两种基本存储结构——邻接矩阵和邻接表在路网导航路径规划中的应用。邻接矩阵虽然直观但空间效率低,不适合表示稀疏图。邻接表则更适用于存储大型稀疏图,如实际的路网,可以有效减少存储空间。在邻接表基础上,通过添加节点标志信息来处理转向限制,提高路径规划的准确性。文章还讨论了Edge结构体的设计,分为路径规划所需信息和额外模块所需信息两部分,以优化内存管理和规划速度。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 2298
2298

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








