反卷积（转置卷积）的理解

网上有很多关于反卷积的资料，这些资料中反卷积的可视化方式对于初学者而言容易产生问题，本小节将对这些问题进行解释说明。

---

一、反卷积的两种可视化

下图是B站吴恩达团队视频中的可视化方式。Filter 与 Input 中的每个像素值分别相乘，得到的结果如右图按位放置，其中重叠区域部分需要相加求和

下图是另一种在博客中常见的可视化方式，即将其视为一种普通卷积。这两种方式看起来不一样，实际上运算过程是等效的。

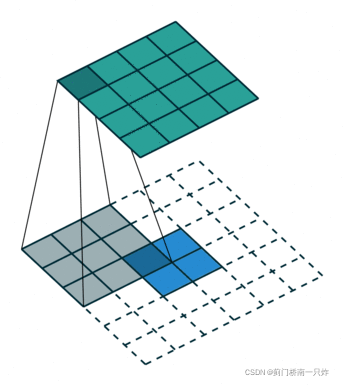
该种可视化方法虽然能将反卷积操作看成普通卷积，便于理解，但由于它是等效得来的，容易对一些细节产生混淆。如果想正确理解反卷积操作，建议采用第一种可视化方法。

二、反卷积的一些易混淆点

1. 卷积核参数位置

上文中提到的第二种可视化中，卷积核在参数位置上需要进行180°旋转才是实际中的卷积核。因为卷积操作会让卷积核参数以180°翻转再乘上某个参数得出结果，因此需要预先对卷积核进行翻转。
具体验证留给读者，可分别采用一二两种可视化计算结果，进行验证。

2. 填充（padding）

padding=0
上图中padding值为0，但是会看到输入的四周还是填充了2个像素，这是由于可视化方式导致的。如果采用第一种可视化方式，会发现确实不存在padding。对于第二种可视化，需要事先填充k-1个像素。

padding>0
对于padding大于0的情况，由于反卷积被视为卷积的反向操作，对于输入的padding则转换为对于输出的center crop，或者直接对卷积核进行padding。例如，padding为2则裁掉output周围的2个像素，也可以将卷积核周围填充2个像素

3. 步长（stride）

stride=1
上图中stride值为1，暂时没有什么问题。

stride>1
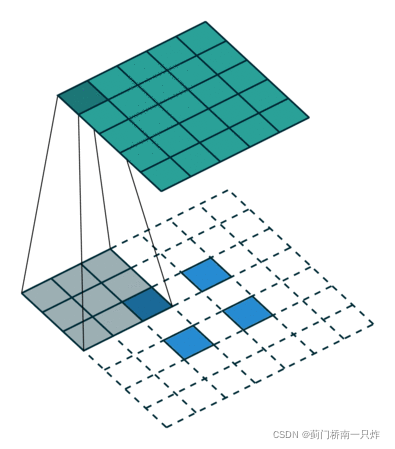
当stride大于1时，等效于在输入各像素之间插入空值，见下图。在第一种可视化方式中，stride则为输出的滑窗步长。在本文的例子中，stride置为2后，滑窗不再有重叠区域，输出大小为4×4。