CDN缓存结点

CDN加速意思就是在用户和我们的服务器之间加一个缓存机制，通过这个缓存机制动态获取IP地址根据地理位置，让用户到最近的服务器访问。
那么CDN是个啥？全称Content Delivery Network即内容分发网络。

CDN是一组分布在多个不同的地理位置的WEB服务器，用于更加有效的向用户发布内容，在优化性能时，会根据距离的远近来选择 。

CDN系统能实时的根据网络流量和各节点的连接，负载状况及用户的距离和响应时间等综合信息将用户的请求重新导向离用户最近的服务节点上，其目的是使用户能就近的获取请求数据，解决网络拥堵，提高访问速度，解决由于网络带宽小，用户访问量大，网点分布不均等原因导致的访问速度慢的问题。

由于CDN部署在网络运营商的机房，这些运营商又是终端用户网络的提供商，因此用户请求的第一跳就到达CDN服务器，当CDN服务器中缓存有用户请求的数据时，就可以从CDN直接返回给浏览器，因此就可以提高访问速度。

CDN能够缓存JavaScript脚本，css样式表，图片，图标，Flash等静态资源文件（不包括html页面），这些静态资源文件的访问频率很高，将其缓存在CDN可以极大地提高网站的访问速度，但由于CDN是部署在网络运营商的机房，所以在一般的网站很少用CDN加速。

我们知道了什么是CDN，那么分发的原理是什么呢？

1. 用户向浏览器提供需要访问的域名；

2. 浏览器调用域名解析库对域名进行解析，由于CDN对域名解析过程进行了调整，所以解析函数库一般得到的是该域名对应的CNAME记录，为了得到实际的IP地址，浏览器需要再次对获得的CNAME域名进行解析以得到实际的IP地址；在此过程中，使用的全局负载均衡DNS解析。如根据地理位置信息解析对应的IP地址，使得用户能就近访问；

3. 此次解析得到CDN缓存服务器的IP地址，浏览器在得到实际的ip地址之后，向缓存服务器发出访问请求；

4. 缓存服务器根据浏览器提供的要访问的域名，通过Cache内部专用DNS解析得到此域名的实际IP地址，再由缓存服务器向此实际IP地址提交访问请求；

5. 缓存服务器从实际IP地址得到内容以后，一方面在本地进行保存，以备以后使用，二方面把获取的数据放回给客户端，完成数据服务过程；

6. 客户端得到由缓存服务器返回的数据以后显示出来并完成整个浏览的数据请求过程。

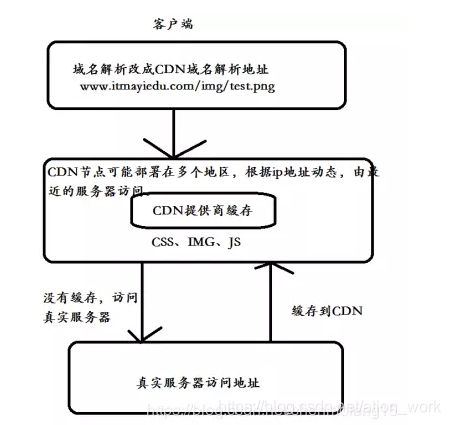
　　使用CDN会极大地简化网站的系统维护工作量，网站维护人员只需将网站内容注入CDN的系统，通过CDN部署在各个物理位置的服务器进行全网分发，就可以实现跨运营商、跨地域的用户覆盖。由于CDN将内容推送到网络边缘，大量的用户访问被分散在网络边缘，不再构成网站出口、互联互通点的资源挤占，也不再需要跨越长距离IP路由了
传统的B/S架构：
　　B/S架构，即Browser-Server（浏览器 服务器）架构，是对传统C/S架构的一种变化或者改进架构。在这种架构下，用户只需使用通用浏览器，主要业务逻辑在服务器端实现。B/S架构，主要是利用了不断成熟的WWW浏览器技术，结合浏览器的多种Script语言（VBScript、JavaScript等）和ActiveX等技术，在通用浏览器上实现了C/S架构下需要复杂的软件才能实现的强大功能。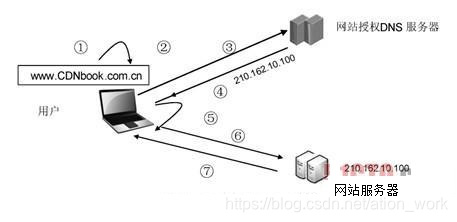

①用户在自己的浏览器中输入要访问的网站域名。
　　②浏览器向本地DNS服务器请求对该域名的解析。
　　③本地DNS服务器中如果缓存有这个域名的解析结果，则直接响应用户的解析请求。
　　④本地DNS服务器中如果没有关于这个域名的解析结果的缓存，则以递归方式向整个DNS系统请求解析，获得应答后将结果反馈给浏览器。
　　⑤浏览器得到域名解析结果，就是该域名相应的服务设备的IP地址。
　　⑥浏览器向服务器请求内容。
　　⑦服务器将用户请求内容传送给浏览器
————————————————
加入cdn后：
　　在网站和用户之间加入CDN以后，用户不会有任何与原来不同的感觉。最简单的CDN网络有一个DNS服务器和几台缓存服务器就可以运行了。一个典型的CDN用户访问调度流程

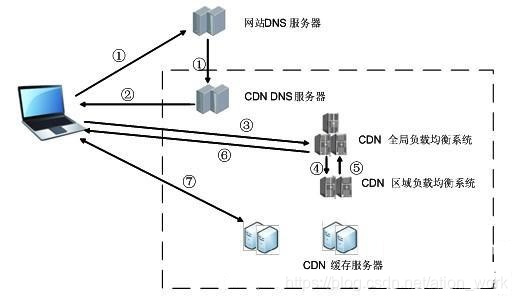①当用户点击网站页面上的内容URL，经过本地DNS系统解析，DNS系统会最终将域名的解析权交给CNAME指向的CDN专用DNS服务器。
　　②CDN的DNS服务器将CDN的全局负载均衡设备IP地址返回用户。
　　③用户向CDN的全局负载均衡设备发起内容URL访问请求。
　　④CDN全局负载均衡设备根据用户IP地址，以及用户请求的内容URL，选择一台用户所属区域的区域负载均衡设备，告诉用户向这台设备发起请求。
　　⑤区域负载均衡设备会为用户选择一台合适的缓存服务器提供服务，选择的依据包括：根据用户IP地址，判断哪一台服务器距用户最近；根据用户所请求的URL中携带的内容名称，判断哪一台服务器上有用户所需内容；查询各个服务器当前的负载情况，判断哪一台服务器尚有服务能力。基于以上这些条件的综合分析之后，区域负载均衡设备会向全局负载均衡设备返回一台缓存服务器的IP地址。
　　⑥全局负载均衡设备把服务器的IP地址返回给用户。
　　⑦用户向缓存服务器发起请求，缓存服务器响应用户请求，将用户所需内容传送到用户终端。如果这台缓存服务器上并没有用户想要的内容，而区域均衡设备依然将它分配给了用户，那么这台服务器就要向它的上一级缓存服务器请求内容，直至追溯到网站的源服务器将内容拉到本地。

　　DNS服务器根据用户IP地址，将域名解析成相应节点的缓存服务器IP地址，实现用户就近访问。使用CDN服务的网站，只需将其域名解析权交给CDN的GSLB设备，将需要分发的内容注入CDN，就可以实现内容加速了。