一种方法论确定6R工业机器人的高性能区域
1 引言
高性能区域(HPA)定义为:工作空间的高性能部分与包含第一关节轴的平面相交的截面[10]。该指标被提出用于衡量工作空间的高性能部分,可为设计者提供关于机器人结构性能的实用信息,同时可为路径规划和工件放置提供指导。
为了确定工作空间中的高性能部分,首先必须选择合适的性能指标,以将该部分与其他区域区分开来。以往的研究中提出了许多性能指标[5,7]。
Yoshikawa 提出了一种基于机器人雅可比矩阵的可操作性度量方法[12]。可操作性度量反映了机器人在任意方向上运动和施加力的能力。条件指标是另一个被定义为雅可比矩阵条件数倒数的度量,用于评估控制精度[8]。其他指标,如最小奇异值、各向同性指标等,在这项工作中得到了详细讨论[7]。
可操作性度量是最常用的性能指标之一[8]。一些研究人员认为,与条件数或最小奇异值相比,可操作性度量是衡量灵巧性更好的指标。因为可操作性度量考虑了末端执行器在所有方向上的运动,而不是一个或两个方向[9]。基于这些思想,我们选择可操作性度量作为性能指标。
确定机器人工作空间的方法有很多,大致可分为两类。解析方法能够确定工作空间边界的闭式描述[11],但这些方法通常较为复杂,因为涉及非线性方程和逆运动学计算[2]。数值方法无需进行逆运动学计算即可获得工作空间的近似边界,且操作更为简便[1,6]。因此,本文提出的方法论将基于数值方法。
2 确定HPA
本部分将详细讨论所提出的方法论确定HPA的整体流程。
由于HPA被定义为工作空间的高性能部分与包含第一关节轴的平面相交的截面,我们可以选择基坐标系的xoz平面作为计算HPA的平面。根据先前的研究可知,可操作性指数不依赖于第一个自由度[4]。因此,为了简化计算,第一关节的关节变量将始终设为0。
2.1 灵巧性度量
机器人的可操作性度量被定义为一个标量值 $ w $,由[12]提出
$$
w = \sqrt{\det(J(\theta)J^T(\theta))}
$$
其中 $ J(\theta) $ 和 $ J^T(\theta) $ 分别为雅可比矩阵及其转置,$ \det $ 表示矩阵的行列式。
如果机器人没有冗余自由度,就像本文中的6R工业机器人的情况一样,上述方程将变为
$$
w = |\det(J(\theta))|
$$
相对于基坐标系的操作雅可比矩阵由[3]给出
$$
{}^0J = [{}^0J_1(q)\ {}^0J_2(q)\ …\ {}^0J_n(q)] \quad \text{with}
$$
$$
{}^0J_1(q) =
\begin{cases}
[z_{l-1} \times {}^{l-1}p_n\ z_{l-1}] & \text{for a revolute joint} \
[z_{l-1}\ 0] & \text{for a prismatic joint},
\end{cases}
$$
其中 $ z_{l-1} $ 是连杆 $ l - 1 $ 的坐标系的z轴向量在基坐标系中的表示,$ {}^{l-1}p_n $ 是连杆 $ n $ 相对于连杆 $ l - 1 $ 的坐标系的位置且在基坐标系中表示,$ \times $ 是向量叉积。
考虑末端执行器后,$ {}^{l-1}p_n $ 在公式(3)中将被替换为 $ {}^{l-1}p_{\text{end}} $。后者是末端执行器参考点相对于连杆 $ l - 1 $ 的坐标系并在基坐标系中表示的位置。
2.2 获取和过滤点云
现在,我们将使用蒙特卡洛方法从一组随机关节向量中获取点云。这些关节向量的每个分量均由以下公式获得
$$
q_l =
\begin{cases}
q_{l,\text{low}} + \text{Rand} \times (q_{l,\text{up}} - q_{l,\text{low}}), & l \neq 1 \
0, & l = 1
\end{cases}
$$
其中 $ q_{l,\text{low}} $ 和 $ q_{l,\text{up}} $ 是第 $ l $ 个关节的下界和上界值,Rand表示0到1之间的随机值。
然后,我们可以通过正运动学方程计算末端执行器参考点的位置和姿态。
$$
T_{\text{end}} = \left( \prod_{l=0}^{\text{dof}} {}^lT_{l+1}(q_l) \right) {}^{\text{dof}}T_{\text{end}}
$$
其中 dof 是机器人具有的自由度,$ {}^lT_{l+1} $ 是相邻连杆 $ l $ 和连杆 $ l+1 $ 坐标系之间的齐次矩阵,$ {}^{\text{dof}}T_{\text{end}} $ 是末端执行器相对于最后一个连杆坐标系的齐次矩阵。
对于由公式(5)计算出的每个点,将计算机器人在该点的雅可比矩阵和可操作性度量。然后引入可操作性度量的阈值来处理这些点。此步骤可用以下公式简单表示:
$$
w =
\begin{cases}
w, & \text{if } (w > h) \
0, & \text{otherwise}
\end{cases}
$$
其中 $ h $ 是阈值,其选择取决于机器人将要执行的任务类型,本文不对此进行讨论。
滤波后,可操作性度量为0的点将被舍弃。
尽管第一个关节变量被设置为0,滤波后的点云中的这些点可能并不位于同一平面上。这是由于末端执行器的存在,其参考点相对于最后一个连杆的坐标系存在平移。
因此,将执行一个变换,将这些点转换到同一平面。该变换由
$$
p_s = [\sqrt{x_w^2 + y_w^2},\ 0,\ z_w]^T
$$
其中 $ p_w = [x_w,\ y_w,\ z_w]^T $ 是变换前滤波后的点云中某一点的坐标,$ p_s $ 是该点在变换后的坐标。
该变换的本质是绕基坐标系的z轴旋转,或者从6R工业机器人的角度来看,是绕第一关节的旋转轴旋转。因此,所有点都将被变换到基坐标系的 xoz平面。
实际上,由于可操作性度量的不变性以及工作空间此前讨论过的对称特性,该变换不会影响我们后续得到的结果。
2.3 网格处理
点云中的所有点现在都位于基参考坐标系的单个平面内,即 xoz平面。为了在该平面内定义一个能够覆盖点云所有点的网格,需要首先确定点云沿 x轴和 z轴的最大尺寸。这两个值可以通过以下公式简单计算得出:
$$
\begin{cases}
X_m = \max_{1 \leq k \leq N}(x_k) - \min_{1 \leq k \leq N}(x_k) \
Z_m = \max_{1 \leq k \leq N}(z_k) - \min_{1 \leq k \leq N}(z_k)
\end{cases}
$$
其中 $ N $ 是滤波后点云中的点数。
现在我们定义一个包含 $ m \times n $ 个单元格的网格,每个单元格的尺寸为 $ \Delta x $ 和 $ \Delta z $,可视为分辨率维度。较小的 $ \Delta x $ 和 $ \Delta z $ 可以获得更精确的结果,但计算成本会更高,因此应选择合适的值。此外,每个单元格将具有0或1的标志值。
每个轴上的单元格数量可以由此推导出
$$
\begin{cases}
N_x = \left\lfloor \frac{X_m}{\Delta x} \right\rfloor + 1 \
N_z = \left\lfloor \frac{Z_m}{\Delta z} \right\rfloor + 1
\end{cases}
$$
其中,算子 $ \left\lfloor \cdot \right\rfloor $ 表示向下取整函数,该函数返回小于或等于括号内实数参数的最接近整数。
创建网格后,我们通过以下方式确定点云中的点 $ p_k $ 将位于网格的哪个单元格中
$$
\begin{cases}
i_k = \left\lfloor \frac{x_k}{\Delta x} \right\rfloor \
j_k = \left\lfloor \frac{z_k}{\Delta z} \right\rfloor
\end{cases}
$$
其中 $ i_k $ 和 $ j_k $ 是单元格 $ n_{i_k,j_k} $ 沿x轴和z轴的索引,即点 $ p_k $ 所在单元格。
然后单元格 $ n_{i_k,j_k} $ 将被着色,其标志值 $ v_{i_k,j_k} $ 将被设置为1。当点云中的所有点都以此方式进行处理完毕后,没有点位于其中的单元格将不会被着色,其标志值保持为0。
2.4 边界提取
为了提取已着色单元格的边界,将应用两步扫描操作。
在第一步中,扫描操作在给定的行内进行,该行的每个单元格都将被扫描以找到第一个和最后一个着色单元格,这些被称为外侧单元格。扫描从单元格 $ n_{0,j} $ 开始,到单元格 $ n_{N_x,j} $ 结束。当我们找到一个其索引 $ i_{j,F} $ 满足以下公式条件的单元格时
$$
\begin{cases}
v_{i,j} = 0 & \text{when } i < i_{j,F} \
v_{i,j} = 1 & \text{when } i = i_{j,F}
\end{cases}
$$
其中 $ v_{i,j} $ 是单元格 $ n_{i,j} $ 的标志值,则该单元格 $ n_{i_{j,F},j} $ 将被视为该行的第一个着色单元格。类似地,当我们找到一个索引 $ i_{j,L} $ 满足以下公式的单元格时
$$
\begin{cases}
v_{i,j} = 0 & \text{when } i > i_{j,L} \
v_{i,j} = 1 & \text{when } i = i_{j,L}
\end{cases}
$$
那么该单元格 $ n_{i_{j,L},j} $ 将被视为该行的最后一个着色单元格。如果某一行的所有单元格均已扫描,但未找到合适的 $ i_{j,F} $ 和 $ i_{j,L} $,则该行将被放弃。
在第二步中,扫描操作在整个网格内进行,每一行都将被扫描,其外侧单元格将被视为构成边界。每行外侧单元格的索引将根据前一行和后一行外侧单元格的索引进行调整。此过程表示为
$$
i_{j,F} =
\begin{cases}
i_{j,F}, & \text{if } j < 2 \text{ or } j > N_z - 2 \
\min(i_{j-1,F}, i_{j+1,F}), & \text{if } i_{j,F} < i_{j-1,F} \text{ and } i_{j,F} < i_{j+1,F} \
\max(i_{j-1,F}, i_{j+1,F}), & \text{if } i_{j,F} > i_{j-1,F} \text{ and } i_{j,F} > i_{j+1,F} \
i_{j,F}, & \text{otherwise}
\end{cases}
$$
and
$$
i_{j,L} =
\begin{cases}
i_{j,L}, & \text{if } j < 2 \text{ or } j > N_z - 2 \
\min(i_{j-1,L}, i_{j+1,L}), & \text{if } i_{j,L} < i_{j-1,L} \text{ and } i_{j,L} < i_{j+1,L} \
\max(i_{j-1,L}, i_{j+1,L}), & \text{if } i_{j,L} > i_{j-1,L} \text{ and } i_{j,L} > i_{j+1,L} \
i_{j,L}, & \text{otherwise}
\end{cases}
$$
此步骤的目的是确保我们得到的边界中没有极端尖锐部分和凹陷部分。
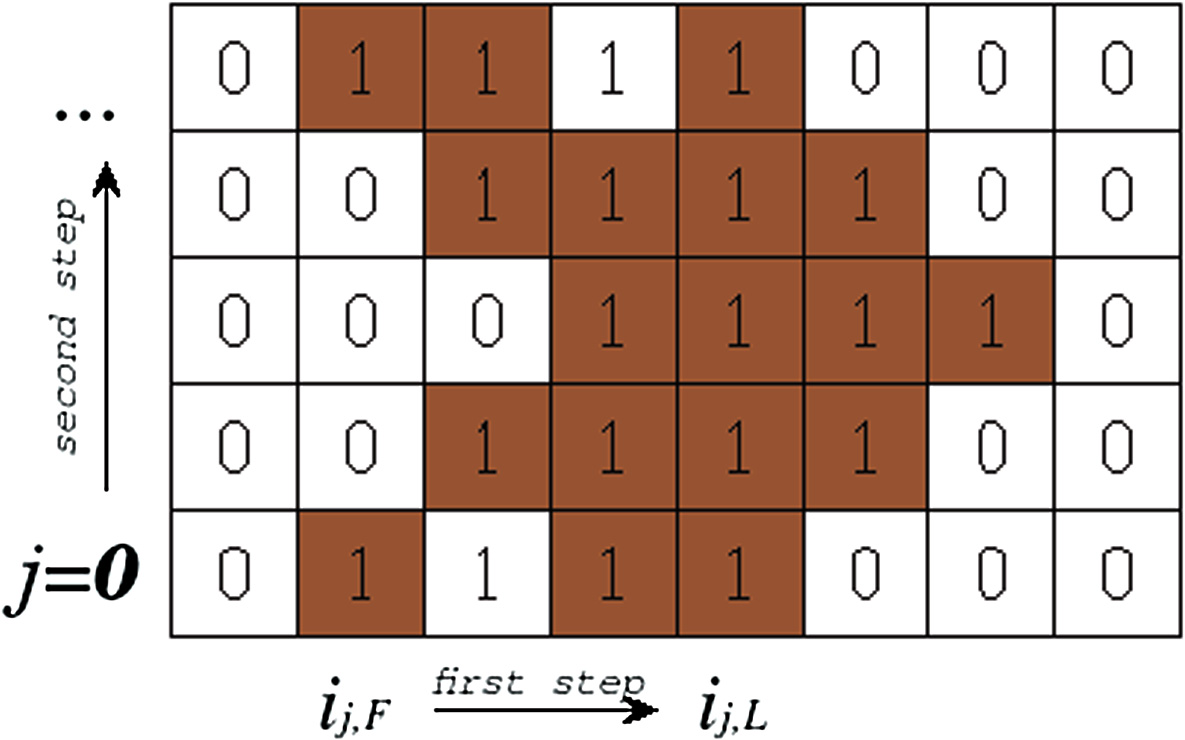
经过上述两个操作步骤后,将计算每一行外侧单元格的中心点,并将其添加到一个数组中,称为边界点数组。按顺序用直线连接该数组中的点,即可得到着色单元格的粗略边界。
2.5 边界平滑
平滑边界的 基本思想是对边界数组中的点使用最小二乘法进行处理。
假设边界点数组中的点数为 $ N_B $。现在我们将这些点划分为 $ N_l $ 个小子点列表,每个列表包含 $ N_p = N_B / N_l $ 个点。对于每个列表,采用最小二乘法确定回归直线。
$$
L_s: \bar{z} = bx + a \quad \text{with}
$$
$$
\begin{cases}
b = \dfrac{\sum_{i=1}^{N_p} (x_i - \bar{x})(z_i - \bar{z})}{\sum_{i=1}^{N_p} (x_i - \bar{x})^2} \
a = \bar{z} - b\bar{x}
\end{cases}
$$
对于两条对应的点列表相邻的回归直线,将计算它们的交点。由于有 $ N_l $ 条回归直线,因此我们将得到 $ N_l $ 个交点。按顺序用直线连接这些交点,即可得到HPA的最终近似边界。此外,将该边界绕第一关节的旋转轴旋转,即可得到工作空间的高性能部分。
一个示例
在本部分中,将通过一个示例来说明所提出的方法论能够有效确定6R工业机器人的HPA。该示例研究的6R工业机器人是莫托曼MH12,其D-H参数由表1给出。
| 连杆 | $ a/\text{mm} $ | $ \alpha/^\circ $ | $ d/\text{mm} $ | $ \theta/^\circ $ |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | −170/+170 |
| 2 | 155 | −90 | 0 | −180/+65 |
| 3 | 614 | 180 | 0 | −85/+150 |
| 4 | 200 | −90 | −640 | −150/+150 |
| 5 | 0 | 90 | 0 | −135/+90 |
| 6 | 0 | −90 | 0 | −210/+210 |
首先,生成了500万个随机点,并对这些点应用了一个阈值。对于需要更高灵巧性的某些应用,如焊接,阈值 $ h $ 应更大,而对于搬运等应用,则适合较小的 $ h $。在本例中,我们不会针对任何特定应用,因此选择了一个适中阈值0.5。

然后创建了一个单元格尺寸为 10 mm × 10 mm的网格。

接着,应用了扫描操作的两个步骤,得到了一个边界数组,并将其点按顺序用直线连接起来。粗略边界如
 所示。
所示。
最后,将边界数组中的点分为100个小列表,并计算其回归线。获得了100个交点,并按顺序用直线连接起来,形成HPA的最终边界,如
 所示。
所示。
整个计算过程在英特尔酷睿i5处理器上耗时约10分钟,其中点云的获取和滤波耗时最长,而网格处理和边界提取相对较快。
此外,通过使用不同的阈值可以获得多个边界。
 显示了从外到内对应的阈值分别为0.5、0.6和0.7的边界。从该图中我们可以大致了解机器人灵巧性的分布情况。
显示了从外到内对应的阈值分别为0.5、0.6和0.7的边界。从该图中我们可以大致了解机器人灵巧性的分布情况。
4 结论
本文提出了一种方法论来确定6R工业机器人的HPA。通过蒙特卡洛方法生成点云,并利用可操作性阈值进行过滤。定义了一个网格以逼近滤波后的点云,然后使用最小二乘法提取并平滑边界。通过一个示例表明,所提出的方法论可用于确定6R工业机器人HPA的可行性。





















 2042
2042

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








