子集，全排列的问题

最新推荐文章于 2025-12-31 21:25:26 发布

原创最新推荐文章于 2025-12-31 21:25:26 发布 · 217 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #leetcode #数据结构

本文详细介绍了解决子集问题及全排列问题的算法实现，包括递归与回溯两种核心方法，并通过代码实例深入剖析了算法的具体应用过程。

这里写目录标题

子集的求解方法
全排列

子集的求解方法

在这里插入图片描述

class Solution {
    int[] nums ;
    public List<List<Integer>> subsets(int[] nums) {
        this.nums = nums ;
        List<List<Ingeter>> Subsets = new LinkedList<>();
        HS(0,Subsets,new LinkedList<Integer>());
        return Substes;
    }
    public void HS(int index , List<List<Ingeter>> Subsets , Linked<Integer> lsit){			//可以按着这个递归走一下，实际上就是暴力递归枚举我认为。但写的又很巧妙。
      		Subsets.add(new LinkedList<Integer>(list));
      		for(int i = index ; i < nums.length ; i ++){
				list.add(nums[i]);
				HS(i+1 , Substs , list);
			}
        }
    }
}

全排列

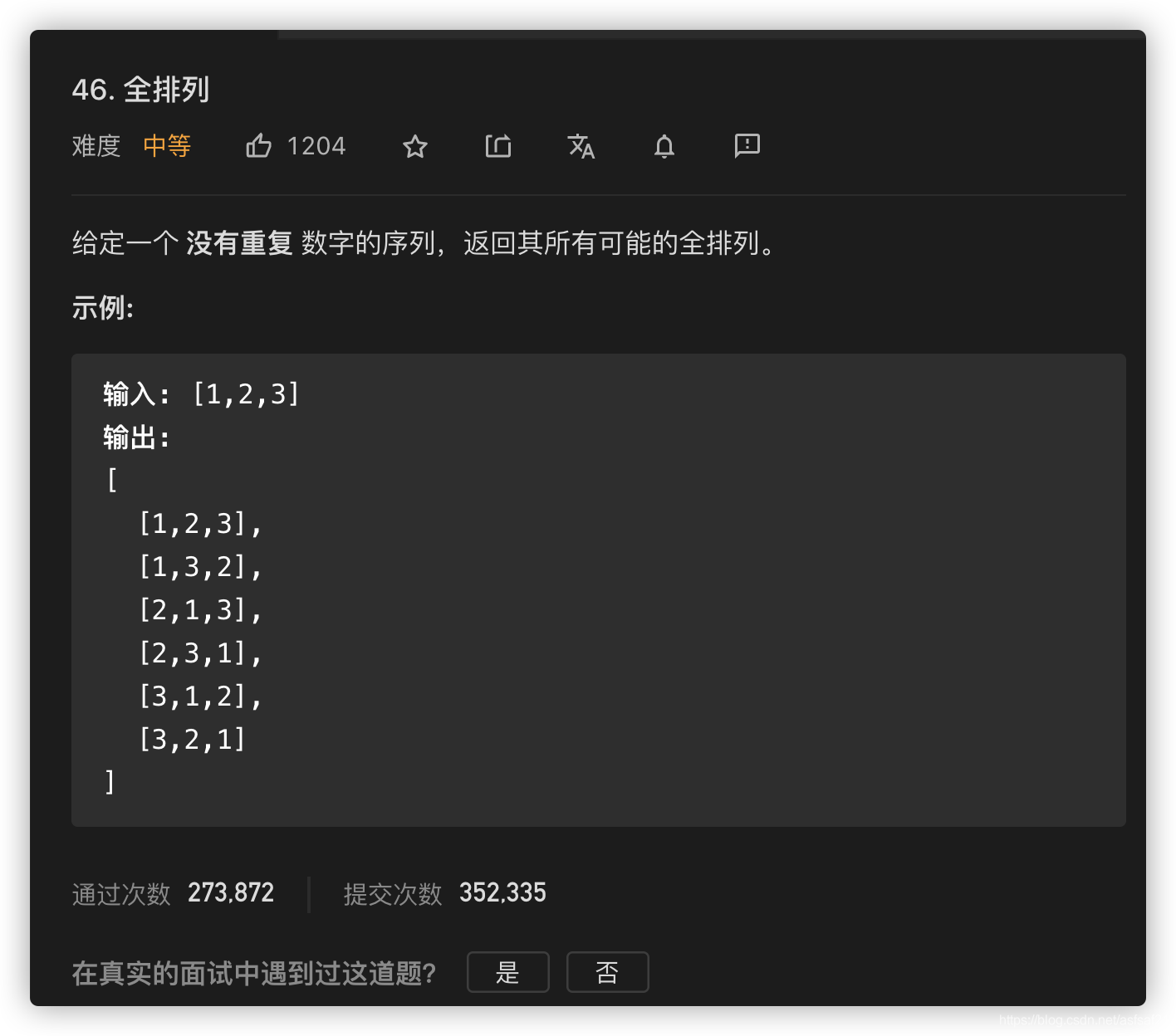在这里插入图片描述这个回溯的过程也可以画图模拟一遍，下次有空了咋们来研究一下。
首先进行算法分析一波：
分析回溯算法------1）
回溯的前提是递归，回溯是更深层次的递归，回溯会存在这样的情况，一旦发生不满足我需求的适合我就会立马撤回到上一层递归，存在撤销等操作我这里分享一个讲的不错的博客文章
链接在这：https://blog.youkuaiyun.com/c_living/article/details/110505841?spm=1001.2014.3001.5501
接下来我简单画一下递归和回溯的流程图，他们是如何返回的如何进一步自我调用的，这种操作都相当耗费栈内存。

在这里插入图片描述

public Solution{
	int[] nums;
	public List<List<Integer>> permute(int[] nums){
		this.nums = nums ;
		List<List<Integer>> Permute = new LinkedList<>();
			//这里我们先把数组拷贝到list集合中方便后续操作
		List<Integer> list = new LinkedList<>();
		for(int n : nums){
			list.add(n);
		}
		HS(0 , Permutr , list);
		return Permute;
	}
	public void HS(int firts,List<List<Integer>> Permute,LinkedList<Ingeter> list){
		for(first == nums.length){
			Permute.add(new LinkedList<Ingeter>(list));
			return;
		}
		for(int i = first ; i < nums.length ; i++){
			Collection.swap(list,first,i);
				//递归建立以first为基准的子排列
			HS(first+1,Permute,list);
				//回溯
			Collection.swap(list,first,i);
		}
	}
}