将奇异值分解应用于缺失值填补

最新推荐文章于 2021-01-17 14:36:05 发布

aohun0743

最新推荐文章于 2021-01-17 14:36:05 发布

阅读量1.4k

点赞数

文章标签：人工智能

原文链接：http://www.cnblogs.com/YSPXIZHEN/p/9546778.html

版权

奇异值分解(SVD)算法常用于矩阵近似，通过分解矩阵为正交矩阵与特征值矩阵的乘积实现。在协同过滤中，SVD用于预测用户评分；在处理缺失值时，选取最大特征值进行矩阵近似，以此填补数据空缺。Frobenius范数用于评估近似度。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

SVD奇异值分解算法：

用于矩阵近似问题。
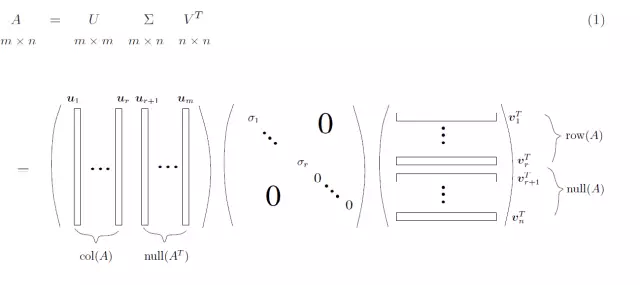
假设矩阵可以分解成三个矩阵的乘积。其中第一个矩阵是一个方阵，并且是正交的，中间的矩阵通常不是方阵，它对角线上的元素都是由原矩阵的特征值构成的，第三个矩阵也是一个方阵，并且也是正交矩阵。
分解时，中间的矩阵不取全部的特征值，而是只取前面若干个最大的特征值，这样就可以对原矩阵进行近似了，两个矩阵之间的近似度一般用Frobenius 范数来衡量，即两个矩阵相应元素的平方差累加再开方。

SVD

应用于协同过滤（预测用户对电影的评分）：

一般来讲，某个用户对电影评分时，会考虑多个因素，比如电影时长，情节设置，剧情等等，不同用户对这些因素的打分一般也是不同的，某用户对某部电影的评分可以看作这些因素的加权组合。
但电影相关的特征很难获取全面，这些特征所依赖的数据很多，可能来自很多因素和源头，对这些特征进行清洗也需要耗费大量的精力。
协同过滤有这样一个假设，即过去某些用户的喜好相似，那么将来这些用户的喜好仍然相似。基于这种思想，奇异值分解可以用于预测用户对电影的评分。