采用两级级联逆变器的汽车推进驱动仿真与测试
摘要
在电动汽车动力总成的生产线上,评估电动驱动系统在标准运行循环下的运行情况是必须的。本文提出了一种专用于汽车应用中电动动力总成性能评估的技术。开发了一个数控实验平台,包括:(i) 由两个直交转换器组成的电力系统,其交流侧通过电抗器连接,以及 (ii) 在NI PXI硬件在环(HIL)测试系统中实现的控制系统。该系统可仿真电动汽车及其动力总成的动态行为。系统分析用于评估稳定性条件,并计算电流纹波及电抗器的最优值。通过对两个案例研究中的汽车驾驶循环进行实验仿真,突显了所开发的汽车测试系统的有效性。同时分析了电动模式和再生制动阶段的功率流。
索引词
汽车驱动测试,硬件在环,测试,实时系统,仿真,道路车辆电力推进,加速,制动。
一、引言
近年来,为了应对全球变暖现象引起的 alarming 气候变化,清洁空气法规不断推动汽车市场采用新型推进系统,其双重目标是:
• 通过电动机高效辅助内燃机(ICE),形成所谓的混合动力推进系统;
• 用电动机替代冰面,形成所谓的电动推进系统。
在此趋势下,汽车行业与学术机构合作,一直并继续参与研发(R&D)项目,主要致力于新型推进系统设计以及在驾驶循环期间对性能优化,重点关注能效和动态行为。此外,针对电动动力总成集成相关的特定问题也已展开研究,旨在:
• 在混合动力系统中,合理分配能量给热力发动机和电动机;
• 延长车辆续航里程。
电动和混合动力汽车动力总成主要由一个或多个电机、一个或多个变速箱、一个或多个电力电子变换器以及诸如电池组之类的嵌入式电源组成。该动力总成在转矩、动态性能和热工况方面运行于严苛的驾驶条件下,其运行性能必须基于标准驾驶循环进行评估。对于此类应用,逆变器需要承担多种功能,同时对减小体积和成本并提高功率输出的需求日益增长。为了实现高性能,逆变器制造商需要简单可靠的终线(EOL)测试系统来评估动力总成功能。
本文的目的是通过一种能够预测驱动器在接近真实条件下的运行情况的实验装置,为电动汽车驱动系统的终检测试提供一种技术解决方案。
从拓扑结构角度而言,用于电力推进逆变器验证的测试台可分为两大类配置。第一类是传统方案,采用由电动机与制动器或发电机机械耦合组成的旋转系统来模拟车辆,从而形成所谓的“测功机测试台”。第二类较不常见的方案则采用电力电子负载来模拟电机。测功机测试台因通常被认为更接近实际情况而被广泛使用。然而,该方案成本效益较低且灵活性有限。事实上,为了测试不同的电机和逆变器,必须更换发电机/制动器及其供电系统,往往需要重新设计整个系统。此外,测功机测试台具有耗散性且需要维护。正是这些因素推动了多个研发项目倾向于选择第二种配置。文献[1]中也指出,在实验环境中,实际负载有时难以甚至无法准确复现。因此,根据开发需求,若企业正在开发完整动力总成(逆变器、电机、齿轮箱等),则测功机测试可能更为合适;而对于仅开发逆变器驱动的企业而言,负载模拟器可能更具优势。它更安全、成本更低、节省空间,维护需求较少,并且在测试不同驱动电机和负载时具有更高的灵活性。
本文的提案属于第二类。它通过在虚拟环境中以实际驾驶工况运行电气动力总成,克服了上述局限性,同时最小化功率损耗和成本。
早期尝试用等效的固态电力电子负载替代机电负载的研究之一是由Slater等人[1]开展的。该负载可灵活控制,以模拟用于在多种应用中测试电力电子变换器的实际系统,从而形成了所谓的“虚拟电机”概念。虚拟电机的主要目标是提供一种模拟的电气负载,使逆变器能够在实际功率水平下进行测试操作,而无需使用真实的电机。虚拟电机的电力电子装置由两个背靠背的三相变流器组成,允许与被测逆变器之间实现双向功率流动。虚拟电机由实时仿真器控制,并编程为可模拟任意电机的行为,且能够修改其参数。实验验证表明,虚拟电机能够准确模拟实际电机的特性。因此,可利用虚拟电机对各种类型的逆变器进行全面测试,从而避免为测试不同逆变器而配置多种类型和额定值的电机。
Monti等人[2],介绍了一种实际应用,即设计一种用于电气驱动系统虚拟测试的创新测试装置。该测试平台由一个在实时模型中仿真的电力电子系统和一个控制系统组成。测试系统的功率部分包括一个无源RLC滤波器、一个由实时仿真控制的逆变器以及一条可实现能量回收的直流母线。针对不同类型电驱动系统的控制律进行了综合设计。
随后,开展了实验研究,考虑了三种驱动器:(i)低功率单相系统,(ii)额定功率低于1kW、用作开发环境的驱动器,以及(iii)采用20kVA逆变器的驱动器。
在[3], Boller和Kennel提出了一种无需实际电机的电驱动应用电压源逆变器测试方法,该实际电机已被虚拟电机替代。已开发出包含功率系统和控制系统的测试台。该测试台由第二个功率逆变器、有源前端、耦合电感以及基于DSP的控制系统构成的控制结构组成。通过对所开发测试台进行实验表明,所提出的虚拟电机具有与实际感应电机相同的特性。论文证明了可以对不同电机及其相应负载进行模拟。被测驱动逆变器可在宽功率范围内运行,且无需对模拟器或其控制单元进行任何修改。
在[4], Monti等人中,开发了一种低成本电力硬件在环(PHIL)平台的创新架构。该架构包括实时仿真引擎、由滤波器和三相逆变器组成的功率部分,以及包含FPGA和数据采集(DAQ)板的信号接口。实验测试证明了所提出结构在模拟机电负载方面的有效性。同时也揭示了一些设计缺陷。该研究提出了一些指导原则以克服这些局限性。
在[5], Grubic等人提出了一种用于逆变器驱动测试台的新型基于电子HIL的概念。电机‐负载传统测试台中的组合已被实现在数字信号处理器(DSP)中的数学模型所取代,该模型用于控制负载模拟器的电力电子部分。耦合网络和一种合适的逆变器拓扑结构,即所谓的“准‐Linverter”,构成了该系统。本文表明,所提出的逆变器拓扑显著降低了输出谐波,从而实现了更好的动态性能。然而,在所开发的测试台上进行的实验表明,LinVerter原型的输出能力限制了速度/负载曲线的实现。现已开发出第二代系统,能够在整个运行范围内重现速度/负载曲线。
在[6], Uebener等人提出了一种包含电机模拟器的测试台,可复现永磁同步电机的功率流。已将电机模拟器的性能与测功机测试台进行了比较。结果表明,对于电动汽车逆变器的测试,电机模拟器是传统测功机测试台的一种低成本替代方案。该电机模拟器由一个受电流控制器控制的多电平逆变器和一个在现场可编程门阵列(FPGA)中编程的电机模型组成。被测逆变器的端子通过耦合电感连接到电机模拟器。利用真实电机的数据构建磁链查表,这些数据来源于有限元分析。在恒定转矩范围内,磁链偏差保持在1%以下,小于大多数电动机的生产公差。
在[7], Casolino等人提出了一种旨在提高成本效益的汽车电动驱动系统测试系统。该工作的主要思想是使用一个电驱动作为被测驱动器的负载。通过三种主要技术对测试逆变器进行控制,并通过仿真进行了比较。对整个测试系统进行了实时(RT)软件在环仿真(SiLS)。特别关注了测试系统的架构和参数调整。如果虚拟负载的参数选择准确,则电机模型在模拟电动汽车行为方面能达到良好的一致性。
在[8],Saito和Akagi中,开发了一种基于两个模块化多电平双星斩波单元(DSCC)变换器的PHIL测试台,这两个变换器以前对前(FTF)配置连接,无需变压器,专用于中压、大功率、高速同步电机驱动。实际被测DSCC逆变器用于驱动虚拟同步电机,进而驱动虚拟负载。该虚拟电机和负载由实际相间辅助电感、实际三相DSCC整流器以及实际双绕组共模电感组成。已开发出一种缩小比例的三相PHIL测试台,并通过实验验证了其性能。将一个三相同步电机作为虚拟电机,并将具有转矩‐速度平方负载特性的虚拟离心压缩机作为虚拟负载。通过实验以及使用PSCAD/EMTDC软件包进行的电路仿真,验证了该PHIL测试台在稳态和暂态条件下的有效性。
在[9],Vodyakho等人提出了一种新型驱动系统拓扑结构,专用于电动驱动系统的原型设计、测试与验证,采用感应电机模拟器而无需使用任何实际电机/发电机。所提出的电机模拟器平台结合了PHIL概念、高保真度电机模型和负载动态特性。电机和负载模型通过实时仿真器进行仿真,生成适当的控制指令发送至电力电子放大器,该放大器与被测可变速度驱动器相连。结果表明,所提出的电机模拟器能够精确复现实际感应电机的运行结果。该概念已在25千伏安功率等级上进行了实验验证。其他类似工作已在[10][11][12][13]中提出。先前的研究主要集中在利用电子负载进行电动机仿真,以实现对功率变换器的电气验证。而本文则提出了一种用于汽车应用的电动驱动系统的新实时PHIL测试系统。本工作中使用的负载是一个标准四象限驱动器,其在实时(RT)下受控,在其端子处模拟实际驱动电动汽车车轮的电机。控制系统不仅包含电机模型,还包括车辆和道路动力学,从而使系统具备在驾驶循环中模拟驱动器真实运行条件的能力。车辆模型通过更改实时模拟器参数即可实现任意类型的电动汽车和道路条件,相比其他类似解决方案,显著提升了系统的灵活性。
电动汽车逆变器按照极为严格的技术规范制造,并需承受极其严苛的运行周期。组件参数或装配公差的微小不确定性很容易导致变流器超出其运行裕度。正如[14],[15],[16],所证明的那样,动力总成部件的温度会呈现复杂的趋势,且取决于驾驶循环;因此,在动态运行过程中,这些温度可能与恒定工况下的温度有显著差异。此外,在将驱动器安装到车辆之前,必须对其控制参数进行精细调整并检查控制操作的正确性。因此,仅在额定电流和频率下测试驱动器的运行不足以评估动力总成的正常工作状态,有必要在实际条件下对驱动器性能进行初步评估。本文讨论了一种用于车辆电驱动系统的测试装置的结构和特性。
第二节介绍了测试台的整体架构,包括电力系统及其数学模型。同时概述了控制系统,包括电机模型、其控制系统以及车辆动力学模型。控制系统向电力系统提供控制信号,以复现电机在功率流两个方向上的端子行为,分别对应加速和再生制动。道路、车辆及电机的参数可实时更改,以实现不同类型车辆和驾驶循环的模拟。第三节分为三个部分:第一部分包含系统分析,旨在根据期望纹波选择扼流电感的取值。
二、测试台布局
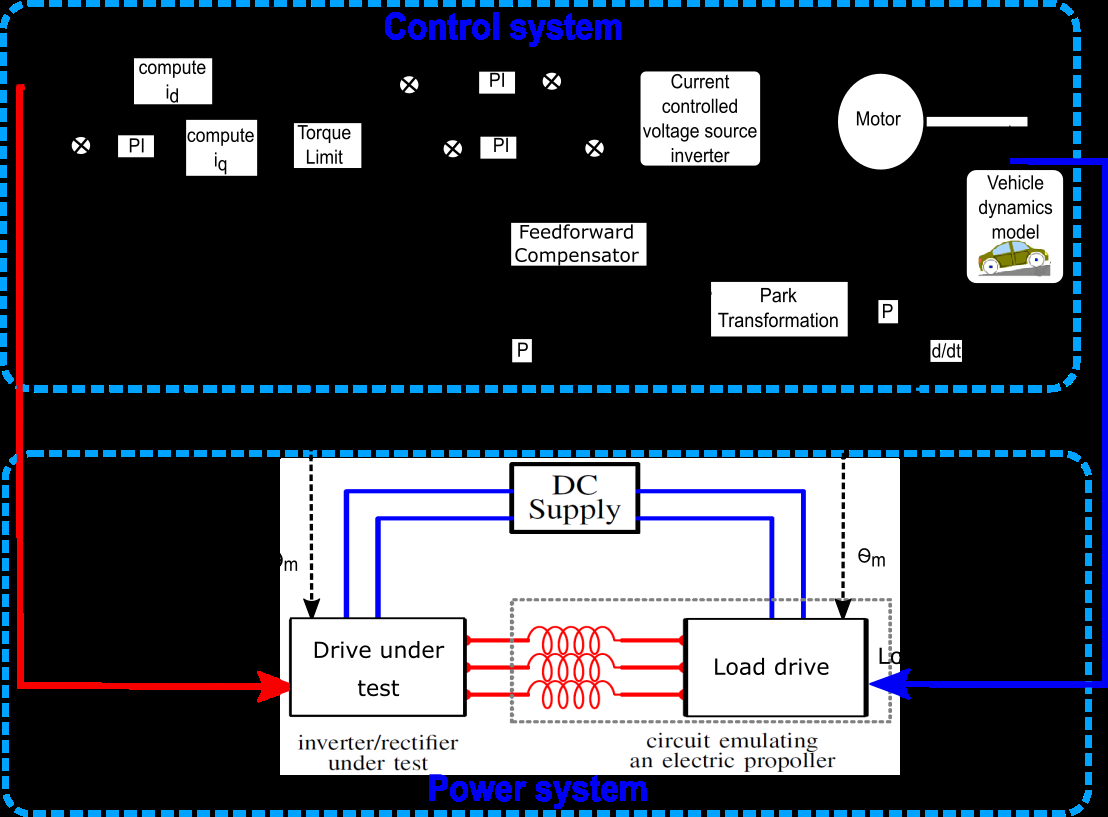
本节介绍了电动汽车推进驱动的实验设置。开发的测试台包括两个主要部分:功率部分和控制系统。这两部分将在下文进行介绍。控制系统的软件由三个主要部分组成,包括电机、矢量控制和车辆。软件及接口在NI PXI系统中实现。对电机和车辆动态性能进行实时且短采样时间的仿真是一项复杂的任务,只有依靠当前最先进的技术才能实现。
A. 电力系统
待测试的驱动器,包括直流/交流逆变器,通过连接两侧交流侧的三相电感器与代表负载的逆变器相连,如图1所示。负载逆变器和三相电感器模拟牵引电机驱动电动或混合动力车辆的车轮。
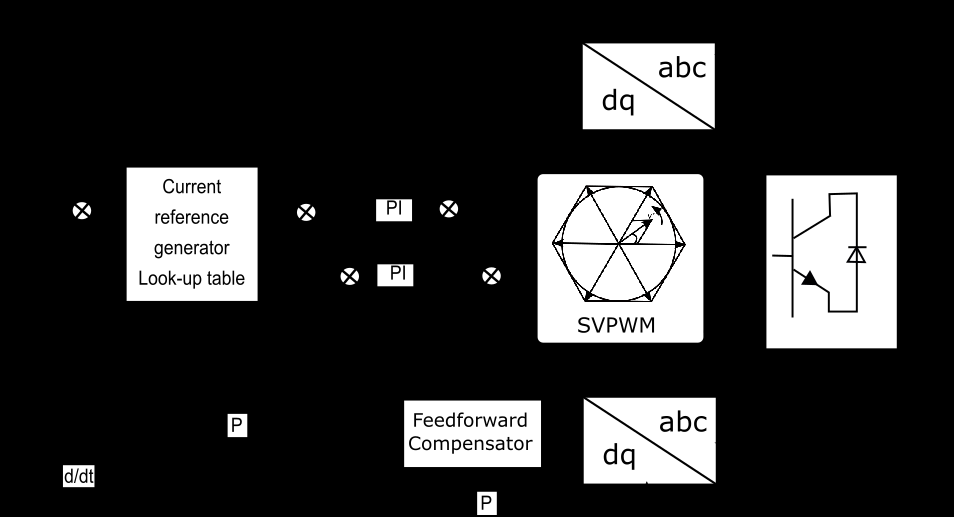
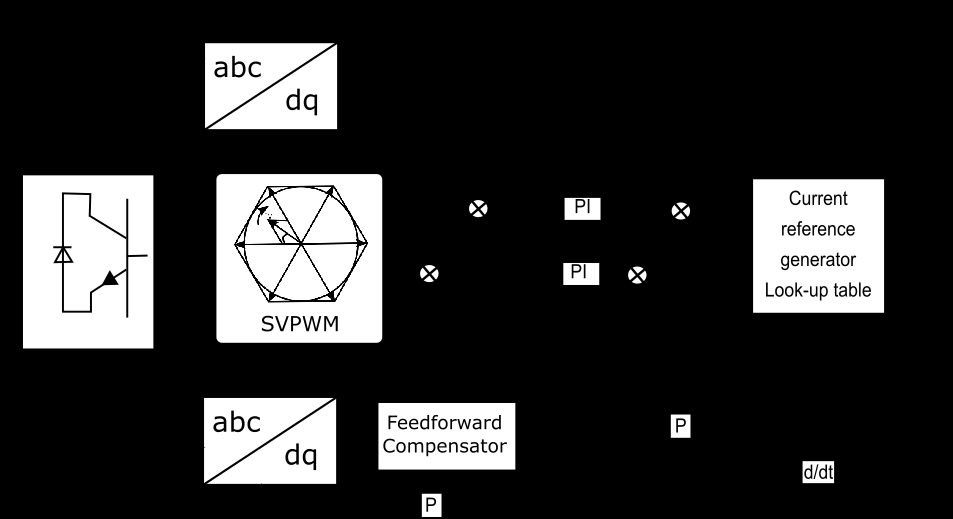
加速时,功率从直流母线流向负载。负载变流器作为整流器运行,功率从其交流侧流向直流母线。再生制动模式时情况相反。图2(a)和图2(b)分别说明了测试系统在加速和再生制动模式下的功率流。
由于构成电力系统的两个变流器均为三相,该电路可视作三个独立的单相电路,每个电路包含一个逆变桥臂。相应的单相等效电路模型如图3所示。该模型由第一个变流器的一个桥臂通过电感连接至第二个变流器对应的桥臂组成。另外两相的特性相同。
直流母线中电流 Iin和 Iout的方向表示功率流动模式。电感中的瞬时电流方向表示支路中的功率流。当左支路提供功率时,电流路径如图3(a)中蓝色所示。电流通过二极管或绝缘栅双极型晶体管的两条可能路径之一,如下方程所示:
$$
\begin{cases}
V_{s22} + V_i + V_{s11} = V_{dc} \
V_{d21} + V_i + V_{d12} = -V_{dc}
\end{cases}
$$
其中 $V_{dc}$为直流母线电压,$V_{si,j}$为功率开关两端的电压,$V_{di,j}$为图2和图3所示二极管两端的反余弦电压。
在图2(b)所示的再生模式期间,电流路径以红色标出,并在图3(a)中显示。电流通过以下方程中的二极管或绝缘栅双极型晶体管(IGBT)走两条可能路径之一:
$$
\begin{cases}
V_{s12} + V_i + V_{s21} = V_{dc} \
V_{d22} + V_i + V_{d11} = -V_{dc}
\end{cases}
$$

电流还可以走另外四种可能路径,其中电感中存储的能量在续流节点处被消耗。其中两条路径如图3(b)所示,并在以下方程中进行分析。另外两条路径在概念上相同,但电流方向相反。
$$
\begin{cases}
V_{s21}+ V_i+ V_{d11}= 0 \
V_{d22}+ V_i+ V_{s12}= 0
\end{cases}
$$
B. 控制系统
控制系统(CS)包括电驱动的矢量控制、电机模型和车辆动力学模型。CS的主要任务是使负载逆变器能够在测试逆变器端子处复现仿真电机的特性。
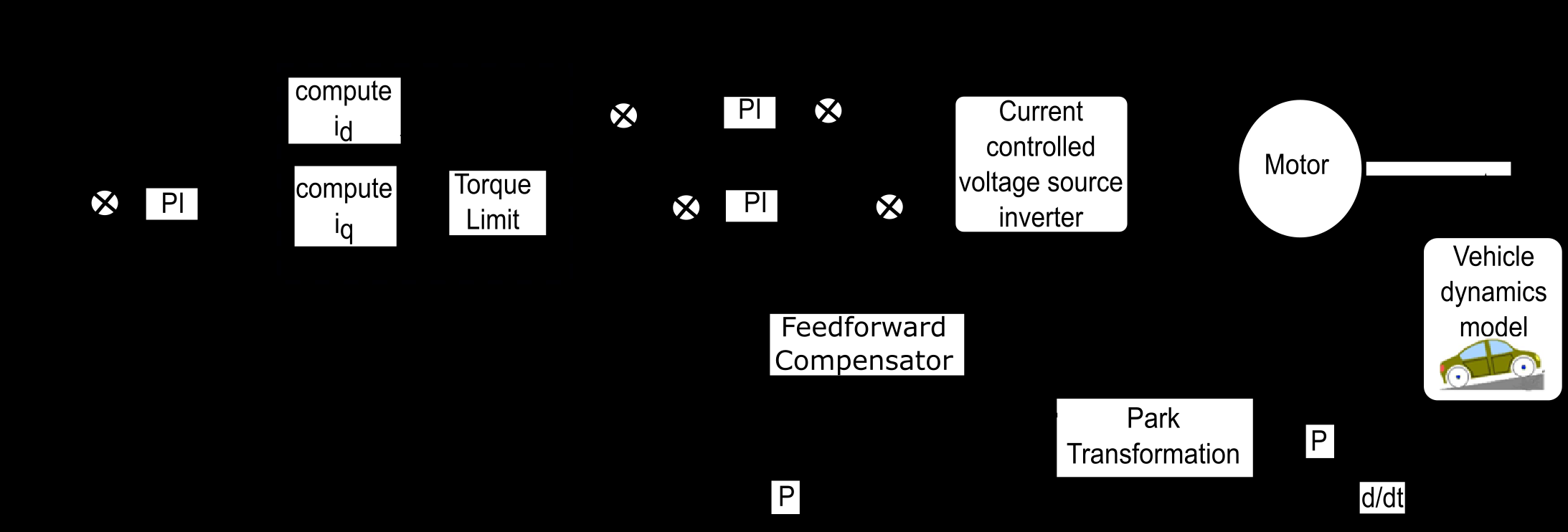
在控制系统中实现的模型是非线性的且紧密耦合,因为它们包含速度和负载转矩作为变量,因此必须同时求解。图4展示了控制方案的一般结构。负载逆变器必须被控制为在驾驶循环期间吸收与模拟驱动器相同的功率,即在相同速度下产生相同的转矩。为了确保实际驱动器与模拟驱动器运行在相同的速度,转子角度通过模拟速度的积分计算得出。
速度。仿真速度是通过求解车辆模型和电驱动模型的机械部分得到的。转子角度的仿真值通过虚拟旋转变压器转换为真实信号。该信号为两个实际驱动器(负载驱动器和测试变流器)提供旋变输入。负载驱动器的转矩参考值为负载转矩。该信号也必须通过仿真生成。负载转矩通过道路/车辆模型的积分获得。负载转矩作为机械平衡方程的一个输入,用于产生速度,如图4所示。该方程的另一个输入是仿真电机的电磁转矩。在该测试台上,仿真驱动器与被测驱动器均为速度控制,其参考信号由控制系统内部生成。
控制系统的功能在NI PXI系统中实现,该系统是一个包含智能接口的实时(RT)平台。控制系统通过三个模拟输出信号与电力系统连接:
• 将要施加到被测驱动器的速度参考信号;
• 计算的转子角度
• 施加到用于模拟牵引电机的驱动器上的转矩参考信号
NI PXI 提供了一个适用于复杂系统实时仿真与控制的虚拟环境。在所提出的测试台中,NI PXI 通过仿真所有可能的汽车循环来测试逆变器在不同驾驶工况下的性能。它为电力系统中的两个变流器提供所需的控制信号,并与主机PC通信,通过可变的系统参数和运行条件实现灵活性。
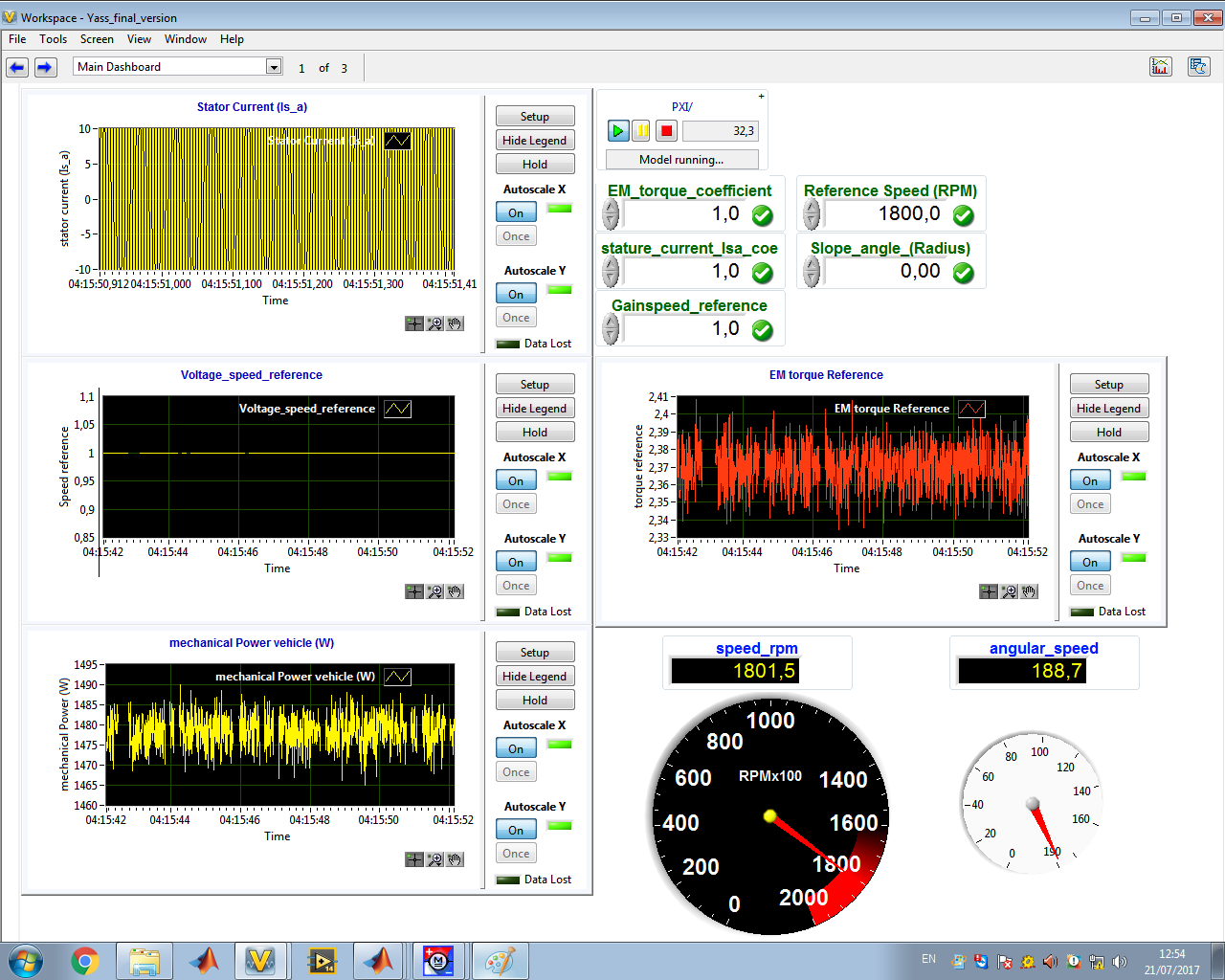
在PXI中实现的控制方案如图5所示,该方案是图4框图的图形化详细表示。它考虑了由电流调节型电压源逆变器供电并驱动电动汽车车轮的永磁同步电机(PMSM)。电驱动器中实现了矢量控制策略。
1) 电机模型
选择永磁同步电机是因其在能效等方面相较于感应电动机具有更高的性能。该PMSM电压方程表达如下:
$$
\begin{cases}
v_d = ri_d + \frac{d\lambda_d}{dt} - p\Omega_m\lambda_q \
v_q = ri_q + \frac{d\lambda_q}{dt} + p\Omega_m\lambda_d
\end{cases}
$$
其中:
• $v_d$和$v_q$是电枢相电压的直轴和交轴分量,
• $i_d$和$i_q$是电枢相电流的直轴和交轴分量,
• $\lambda_d$和$\lambda_q$是电枢相磁链的直轴和交轴分量,
• $r$是电枢相电阻,
• $\Omega_m$是转子速度,
• $p$是极对数。
电枢相磁链的直轴和交轴分量用$i_d$和$i_q$表示如下:
$$
\begin{cases}
\lambda_d = L_di_d + \lambda_{pm} \
\lambda_q = L_qi_q
\end{cases}
$$
其中:
• $L_d$是d轴内的电枢电感,
• $L_q$是q轴内的电枢电感,
• $\lambda_{pm}$是永磁体磁链,也称为空载磁链。
该模型的机械方程如下:
$$
T_{em} - aT_L = J_a \frac{d\Omega_{wh}}{dt} + D\Omega_{wh} \frac{1}{a}
$$
其中:
• $J$ 和 $D$ 分别为惯性和阻尼系数,
• $T_L$ 是电机的负载转矩,实际上是车轮轴上的牵引转矩;
• $T_{em}$ 是永磁同步电机产生的电磁转矩,其中:
$$
T_{em} = p(\lambda_d i_q - \lambda_q i_d)
$$
• $a$是齿轮箱的减速比;
• $\Omega_{wh}$是驱动轮速度。
达朗贝尔方程公式6提供轮速作为车辆动力学系统的输入。车辆动力学模型提供负载转矩 $T_L$的值。
2) 矢量控制
已实现标准的内置式永磁电机矢量控制[18]。然而,通过选择$id= 0$和$Ld= L q$,同一方案也可用于控制表面贴装式永磁电机。在恒定转矩区域和弱磁区域中,控制技术有所不同。该控制技术的框图如图5所示。在基速以下时,采用最大转矩每安培(MTPA)控制。$i_d$分量的计算公式为:
$$
i^*
d = \frac{\lambda
{pm}}{2(L_q - L_d)} - \sqrt{\frac{\lambda^2_{pm}}{4(L_q - L_d)} + i^2_q}
$$
采用这种控制技术,当$i^*_d$电流参考达到时,可实现最大转矩
$$
i^*
{d,a} = \frac{\lambda
{pm}}{4(L_q - L_d)} - \sqrt{\frac{\lambda^2_{pm}}{16(L_q - L_d)} + i^2_{max}}
$$
最大电流:
$$
i_{max} = \sqrt{i_{d*}^2 + i_q^2}
$$
中间电压指令 $v_{id}$和$v_{iq}$由两个PI调节器提供。为了消除交叉耦合效应并线性化电流控制环路,考虑使用前馈补偿器,如图5[18][19]所示:
$$
\begin{cases}
v_{d0} = -p\Omega_m L_q i_q \
v_{q0} = p\Omega_m (\lambda_{pm} + L_d i_d)
\end{cases}
$$
参考电压$v^ _d$和$v^ _q$随后被获得为:
$$
\begin{cases}
v^
d = v
{id} + v_{d0} \
v^
q = v
{iq} + v_{q0}
\end{cases}
$$
基速以上,如果达到转矩极限,则激活弱磁控制。参考值$id^*$的计算如下:
$$
i^*
d = -\frac{\lambda
{pm}}{L_d} \pm \frac{1}{L_d} \sqrt{\left(\frac{V_{out}}{p\Omega_m}\right)^2 - (L_q i_q)^2}
$$
其中 $V_{out}$为相电压的极限值。在最大转矩电流比(MTPA)和弱磁区域,使用式8和式13计算$id$。将转矩参考值$T^ _{em}$作为输入,由式7和式8或式7和式13构成的系统可提供电流参考值$i^ _d$和$i^ _q$。在商用驱动器中,$i^ _d$和$i^*_q$与转矩参考值之间的关系通过查表法实现。
3) 车辆动力学
车辆模型在系统中起着关键作用,因为它能够实现特定车辆的动态性能。该模型以车轮角速度为基础进行建模,并考虑了可在实时(RT)条件下修改的车辆和道路参数。基于[21],已在[20]中开发了一个简化的车辆模型。车辆模型的输出为公式6中的负载转矩。
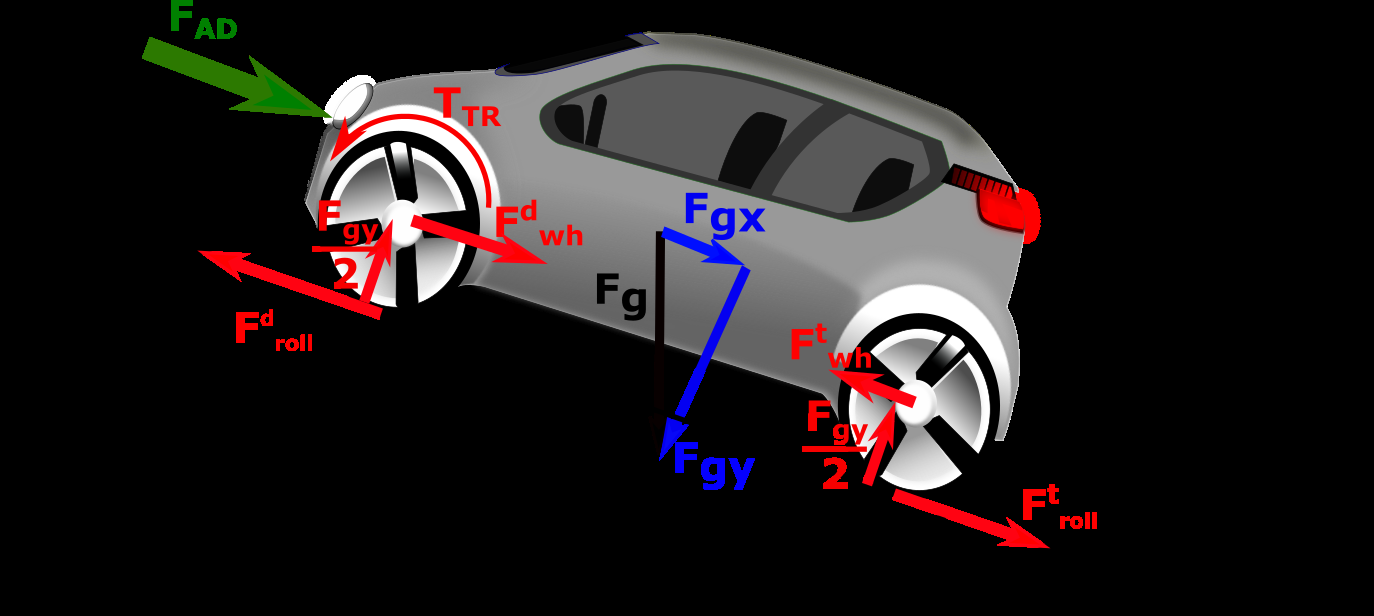
该模型考虑了纵向力和垂向力,未包含侧向(转弯)力。车辆动力学模型如图6所示,考虑了半车模型。应用了三个力平衡:
• 作用在驱动轮上的力和转矩的平衡;
• 作用在拖车轮上的力和转矩的平衡;
• 作用在车辆底盘上的纵向力的平衡。
该模型考虑了车辆重量、道路坡度、牵引转矩、摩擦以及空气动力。所推导的模型包含一些常数,这些常数是车辆和道路的特征参数。滚动阻力是由轮胎材料(尤其是橡胶)中发生的非弹性效应引起的。产生滚动阻力的主要原因是迟滞效应,但也包括其他效应,如塑性变形和轴承摩擦。此处,滚动阻力被分解为其垂直分量$F_{roll, y}$,其作用线相对于车轮轴偏移了距离$b$,以及纵向分量$F_{roll,x}$,后者主要是由滑移引起的。方程的建立基于半车重量均匀分配到驱动轮和拖车轮的假设。在下文中,驱动轮为前轮。
驱动轮受到电机通过变速机构在其轴上施加的牵引转矩$T_{TR}$,该转矩被滚动阻力$F_{d roll,x}$和$F_{roll, y}$以及惯性转矩所平衡。
因此,驱动轮车轮轴上的转矩平衡为:
$$
T_{TR} - F_{d roll,x}R - \frac{F_{g,y}}{2} b = J_{wh} \frac{d\Omega^d_{wh}}{dt}
$$
其中,$b$为轮轴与压力曲线中心之间的距离,$\Omega^d_{wh}$为驱动轮速度,$J_{wh}$为驱动轮的转动惯量,$R$为轮胎的外半径,$F_{g,y}$为车辆重量的法向分量。在公式14中,滚动阻力的纵向分量取决于路面与车轮之间的摩擦系数$\mu_d$,其关系如下:
$$
F_{d roll,x} = \mu_d(\sigma_d)\frac{F_{g,y}}{2}
$$
其中$\sigma_d$是驱动轮相对滑移,定义为:
$$
\sigma_d = \frac{\Omega^d_{wh}R - V}{\Omega^d_{wh}R}
$$
且$V$是车辆速度。
路面‐车轮相互作用通常通过摩擦系数来考虑。Pacejka模型[22]按如下方式计算摩擦系数$\mu$:
$$
\mu(\sigma) = D \sin(C \arctan(B\sigma - E(B\sigma - \arctan(B\sigma))))
$$
其中,$B$、$C$、$D$、$E$为表征道路状况的参数。不同类型道路的这些参数值见表I。
| B | C | D | E |
|---|---|---|---|
| 干燥路面 | 10 | 1.9 | 1 |
| 湿地路面 | 12 | 2.3 | 0.82 |
| Snow | 5 | 2 | 0.3 |
| Ice | 4 | 2 | 0.1 |
作用在驱动轮上的纵向力的平衡为:
$$
F_{d roll,x} - F_{d wf} = M_{wh} \frac{dV}{dt}
$$
其中$F_{d wf}$是底盘对轮轴的反作用力。
施加在驱动轮$T_r$上的总阻力矩通过以下关系获得:
$$
T^d_r = 2F_{d roll,x} R + F_{g,y} b
$$
在拖车轮中,不存在电机转矩,因此转矩平衡方程简化为滚动阻力之间的平衡:
$$
F_{t roll,x} R - \frac{F_{g,y}}{2} b = J_{wh} \frac{d\Omega^t_{wh}}{dt}
$$
其中,$\Omega^t_{wh}$是拖车轮的角速度,由于滑移率不同,其与驱动轮的角速度有所差异。
即使在公式20中,滚动阻力的纵向分量也取决于摩擦系数$\mu_t$,它是滑移$\sigma_t$的函数:
$$
F_{t roll,x} = \mu_t(\sigma_t) \frac{F_{g,y}}{2}
$$
其中$\sigma_t$是拖车轮的相对滑移,定义为:
$$
\sigma_t = \frac{\Omega^t_{wh}R - V}{R\Omega^t_{wh}}
$$
拖车轮扭矩平衡用于计算滚动阻力的纵向(x)分量,因为车辆速度由驱动轮决定。许多模型未考虑拖车轮扭矩平衡,而是仅关注单个驱动轮。这些模型被称为四分之一车模型或e‐corner模型。
作用在拖车轮上的纵向力的平衡为:
$$
-F_{t roll,x} + F_{t wf} = M_{wh} \frac{dV}{dt}
$$
其中$F_{t wf}$是底盘对拖车轮轴的反作用力。
作用在车辆底盘上且沿运动方向平行的纵向力的模型为:
$$
F_{d wf} - F_{t wf} - F_{AD} - F_{g,x} = \frac{M}{2} \frac{dV}{dt}
$$
$F_{d wf} - F_{t wf}$是净牵引力,$F_{AD}$是空气动力,$F_{g,x}$是车辆重量的纵向分量,$M$是车辆质量。
空气动力$F_{AD}$是速度平方的函数,表达式如下[23]:
$$
F_{AD} = \frac{1}{2}(\rho C_x S_t (V + V_a)^2)
$$
其中$\rho$为空气密度,其值为1.225kg/m²,$C_x$为取决于车身形状的阻力系数,$V_a$为气流速度,$S_t$为车辆的最大迎风面积,单位为m²。
车辆模型根据车轮角速度计算阻力矩,同时考虑道路坡度角以及车辆和道路参数。由方程14、18、20、23、24组成的系统是一个包含五个未知数$T_r$、$F_{d wf}$、$\Omega^t_{wh}$、$F_{t wf}$、$V$的五个方程的系统。四分之一车的框图如图7所示。
C. 将电力系统与控制连接
如第二节A部分所示,该电力系统复制了驱动系统的运行,其中被测变流器为三相负载变流器供电。该负载变流器仿真一个永磁同步电机,用于驱动电动或混合动力汽车的车轮。
如图9所示,电力系统通过两个模拟信号与控制简单接口连接:
• 参考速度,即被测驱动器速度环的输入,如图10所示;
• 车辆动力学模型提供的负载转矩 $T_L$,用于控制负载驱动器的转矩环,如图11所示。
为了简化并提高成本效益,将转子角度传递给虚拟速度传感器,该传感器是一种定制硬件,可将数字计算角度转换为与真实编码器/解算器接口兼容的模拟信号。虚拟速度传感器连接到测试逆变器和负载逆变器的编码器/解算器输入端。永磁同步电机转子位置$\theta_m$由编码器模拟器提供给两个驱动器。图9显示了该系统的总体框图。
需要注意的是,电动汽车通常采用转矩模式进行控制,尽管大多数电动汽车驱动系统也包含用于巡航控制和其他特殊功能的速度指令。为了实现稳定性,其中一个驱动器必须进行速度控制,另一个则应进行转矩控制。在当前测试台的实现中,我们选择向负载驱动器提供转矩参考值,以允许被测驱动器执行指定的驾驶循环。
为了实现测试系统的实时控制,设计了两个图形界面,具体描述如下:
• 主仪表板的布局如图12所示。它能够对选定的驱动变量进行实时控制,例如输入量(参考速度和道路坡度角)。它还可以以转/分和弧度/秒(圆形刻度)显示速度、电枢相电流、负载转矩以及负载所需的机械功率,
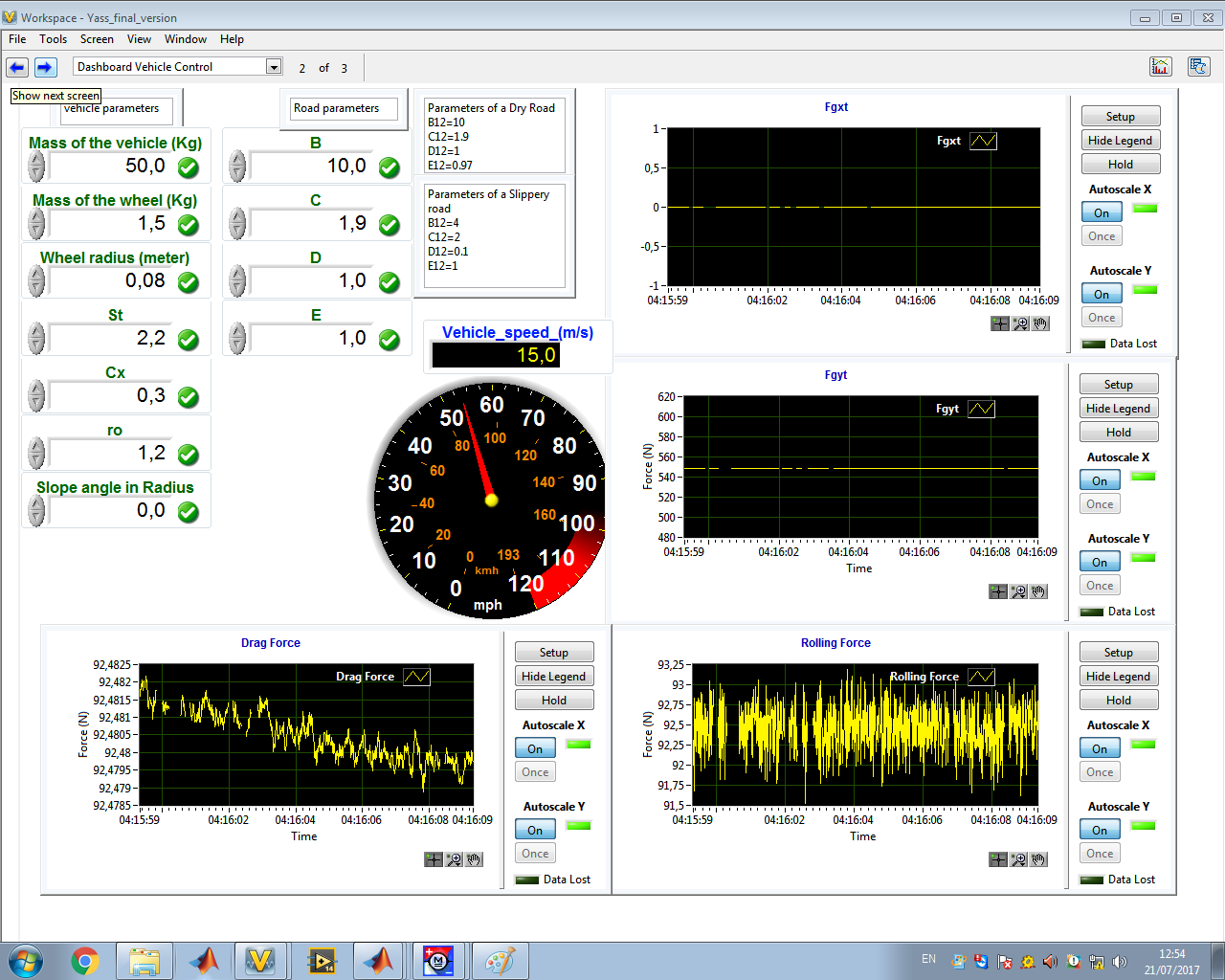
• 车辆控制面板的布局如图13所示。它提供了修改车辆模型中某些变量的可能性,例如质量、车轮半径和道路参数。此外,它还能在线监控车辆动力学模型中考虑的空气阻力、滚动阻力、重力以及车辆速度。
三、分析
A. 电感计算
除了在汽车传动系统仿真中的作用外,三相电感还能防止两个变流器之间的短路,并减小负载输入端的电流纹波。电流纹波应调整至与模拟电机的实际运行情况相匹配。本节致力于预测连接两个变流器的电路中电感和电阻的取值,以使负载电流尽可能平滑。
考虑电感的一相,描述由式1‐3表示的RL电路的微分方程表达为:
$$
\pm V_{dc} - V_{drop} = Ri + L \frac{di}{dt}
$$
其中$V_{drop}$是导通的二极管和开关上的电压降,$i$是RL电路电流。考虑到电流的初始值$i_0$,方程(26)的解为:
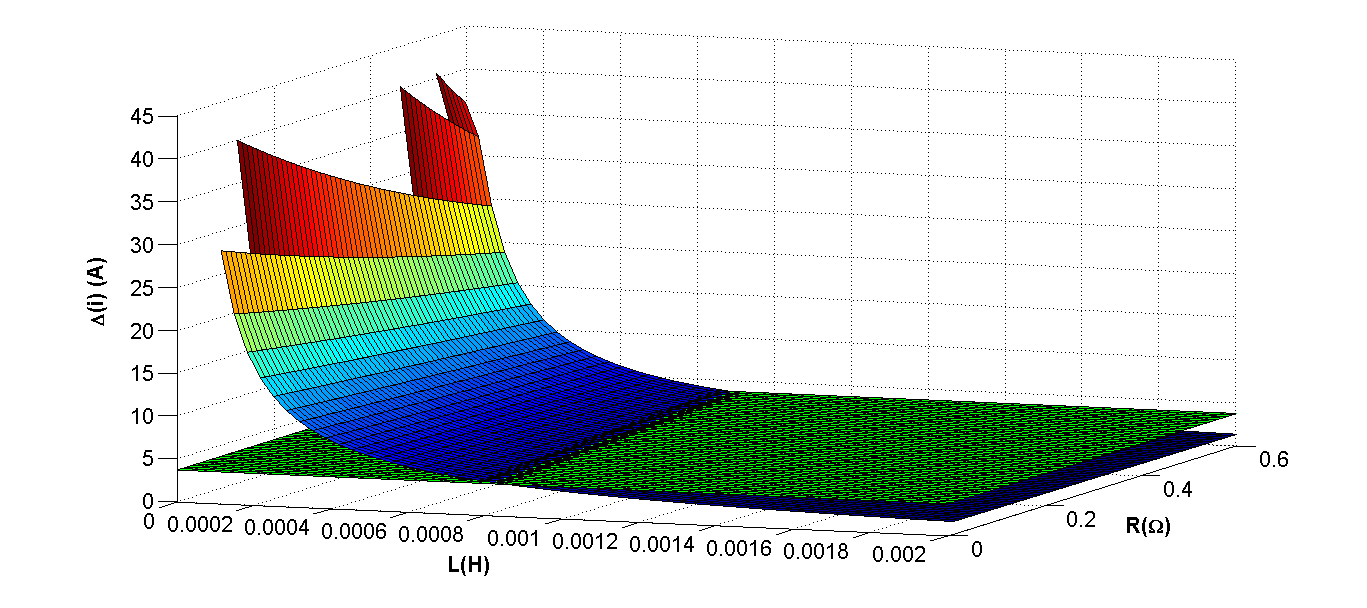
 随 L和 R在 8kHz开关频率下的变化。绿色平面对应于正弦电流引起的电流变化。)
随 L和 R在 8kHz开关频率下的变化。绿色平面对应于正弦电流引起的电流变化。)
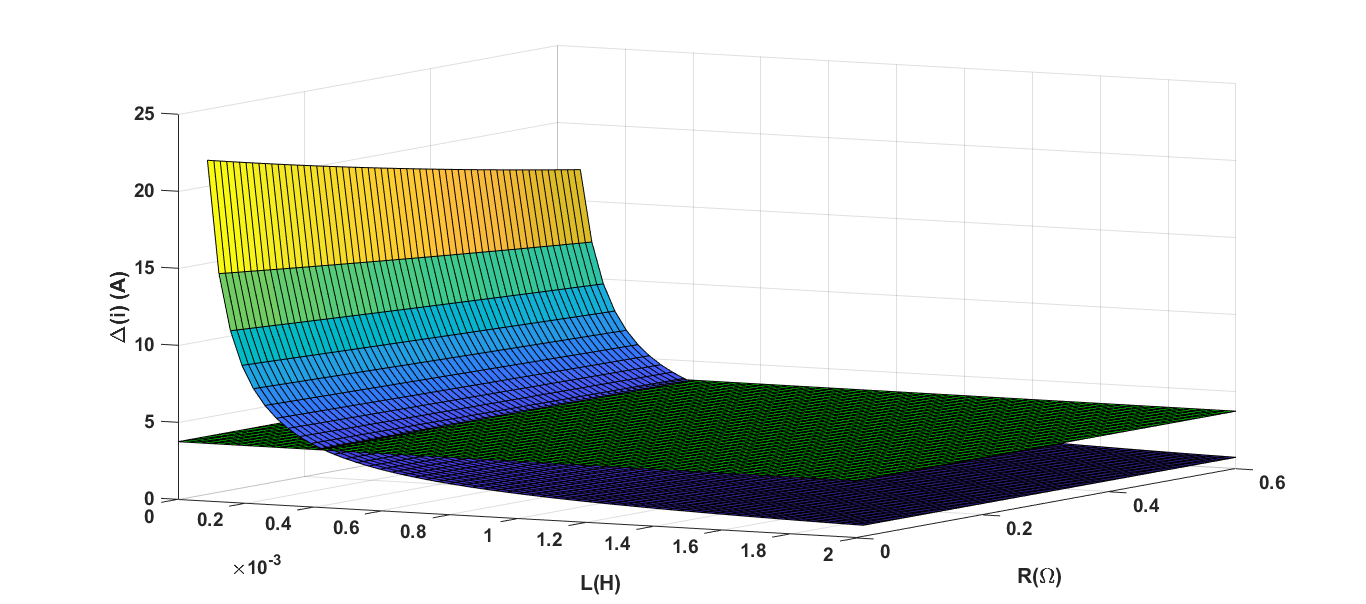
 随 L和 R在 16kHz开关频率下的变化。绿色平面对应于正弦电流引起的电流变化。)
随 L和 R在 16kHz开关频率下的变化。绿色平面对应于正弦电流引起的电流变化。)
$$
i(t) = i_0 e^{-(R/L)t} + I(1 - e^{-(R/L)t})
$$
其中$I$是$i$的渐近值:
$$
I = \frac{V_{dc} - V_{drop}}{R}
$$
两个逆变器的功率开关在一个开关周期$\Delta(t)$内的电流变化可表示为:
$$
\Delta(i) = i(\Delta(t)) - i_0 = (I - i_0)(1 - e^{-(R/L)\Delta(t)})
$$
为了在正弦稳态下实现无纹波电流,电流变化$\Delta(i)$应满足以下方程:
$$
\Delta(i)’ I_L \sin(\omega_L \Delta(t))
$$
其中$I_L$和$\omega_L$分别为负载电流的最大值和角频率。
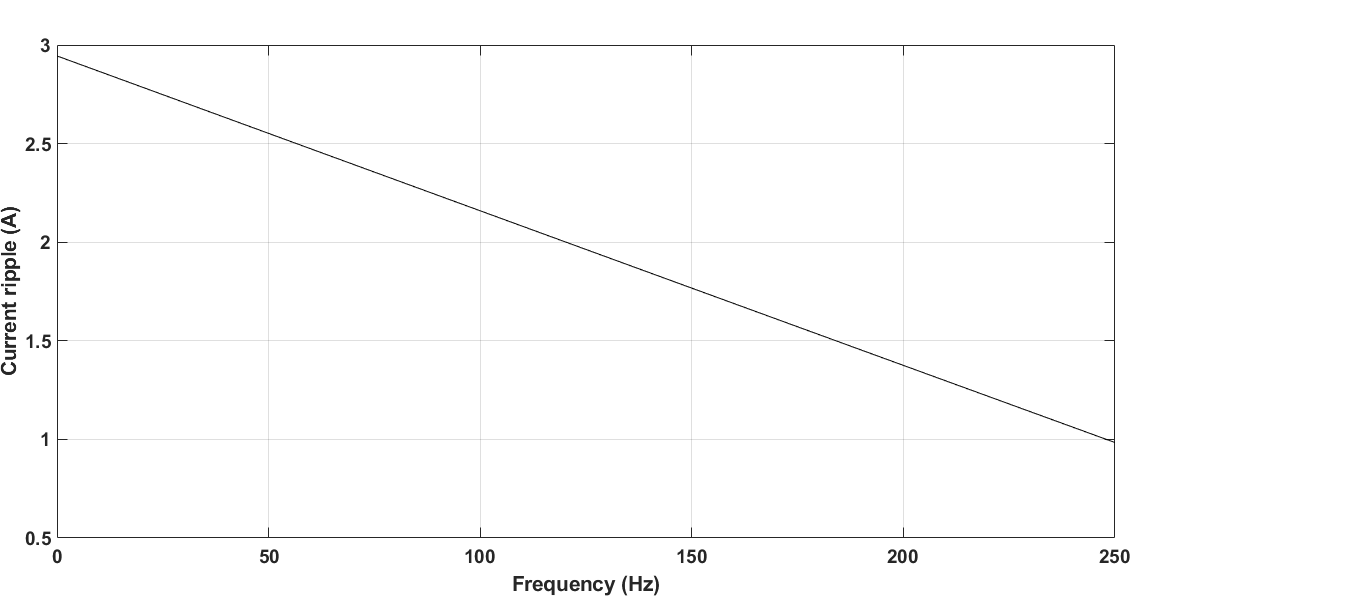
图14和图15显示了在负载逆变器不同开关频率下,给定$I_L$和$\omega_L$值时,$\Delta(i)$相对于$L$和$R$的三维图。绿色平面对应于正弦电流引起的电流变化$\Delta(i)_{\text{sin}}$。显然,负载逆变器的开关频率较高值会导致电感的较低值。必须考虑到两个逆变器的开关时刻并未同步。因此,当两个开关频率相同时,平均开关周期应为
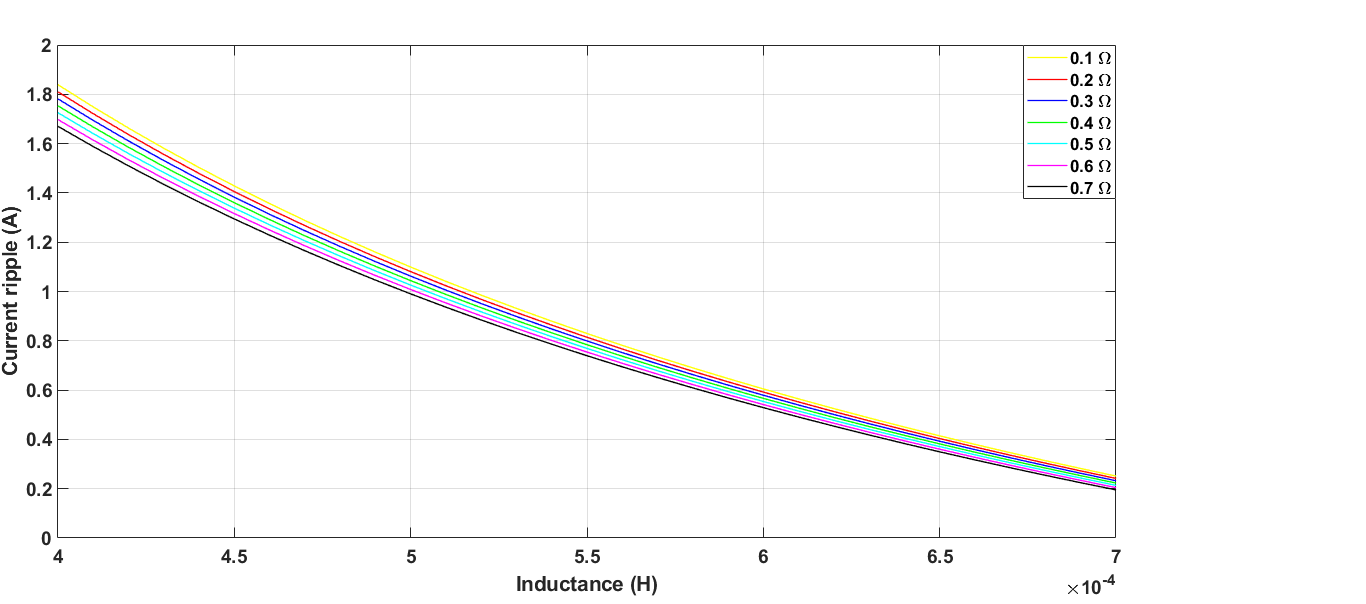
 随 L在不同 R值时的变化情况。)
随 L在不同 R值时的变化情况。)
考虑的开关时间是一半,因为一个逆变器的每个开关区间都包含另一个逆变器开关的一次换相。如果两个开关频率不同,则合成频率可取两者之和。对于大功率驱动器,必须减小电抗器的尺寸,以控制测试设备的质量和成本。因此,以比测试逆变器更高的开关频率来控制负载逆变器将是有利的。
参考图14和图15,可以看出对于每个开关频率,都存在一组参数($R$,$L$),其对应于三维图与绿色平面相交处的点,在这些点上$\Delta(i)$的变化呈正弦形状。
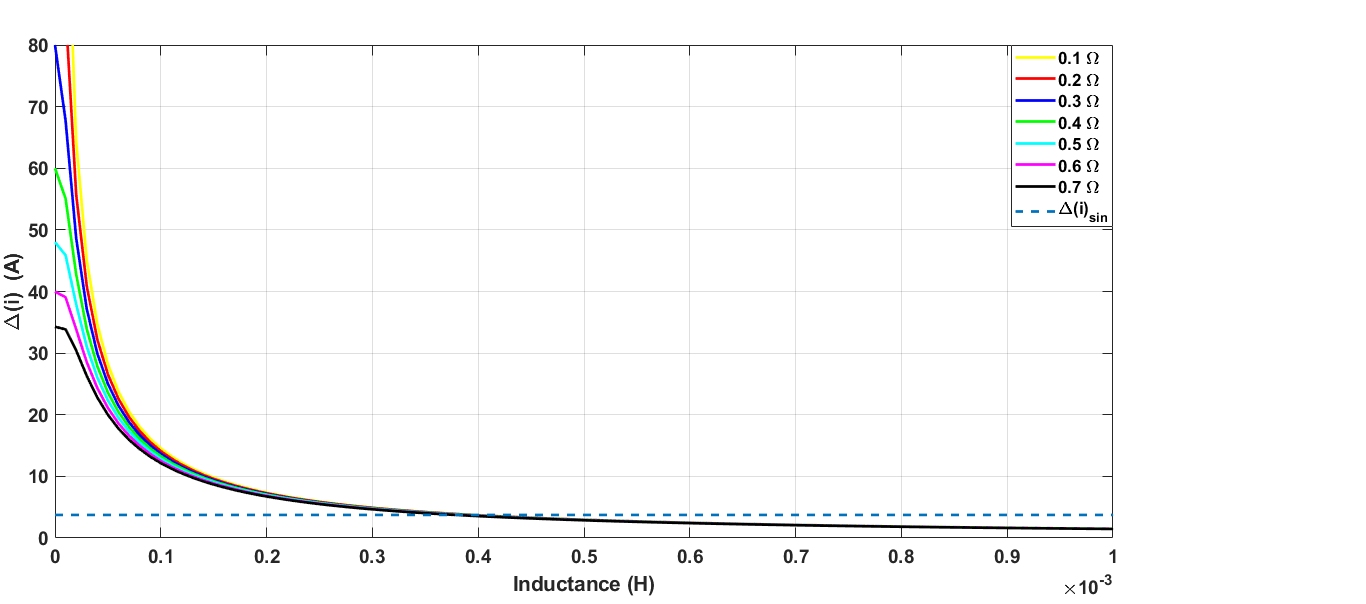
为了准确选择($R$, $L$)的组合,已考虑在16kHz开关频率下针对不同$R$值的$\Delta(i)$随$L$变化的二维图。根据图16,对于电感值在0.2 ÷ 0.4mH范围内的多种电阻情况,$\Delta(i)$接近于$\Delta(i)_{\text{sin}}$。然而,为了使电流纹波$\Delta(i)$更接近实际驱动的值,需根据实际驱动的纹波将$L$选在0.3mH附近。
B. 电流纹波评估
将公式29减去公式30,可对电流纹波进行评估。利用第三节III‐A中的参数,得到电流纹波。
可根据电流纹波随电感值的变化特性来优化电抗器,在16kHz开关频率下不同电阻值时的特性如图17所示。增加电感会导致出现负值,意味着电流无法在一个采样时间内达到期望的设定值。最后,图18显示了电流纹波随电源(调制)频率变化的趋势。频率越高,纹波越小。
C. 稳定性分析
通过分析传递函数的根来评估电力系统的稳定性。所分析的系统由电流控制下的两个驱动器组成
环路级别。通过建立子系统的传递函数,即两个逆变器和电感(扼流圈)的传递函数,得到电力系统的框图。两个驱动器的输入是电流参考值的直轴和交轴分量。如小节II‐B2和II‐C所述,电流参考值$i^ _d$和$i^ _q$与实际电流值$i_d$和$i_q$之间的误差$e_1$和$e_2$被送入两个PI调节器。
由于$i_d$和$i_q$电流的调节方式相同,因此可以只关注其中一个分量,该分量将如图19中所示通用表示为$I$。
扼流圈两端的电压是逆变器之间的差值电压。扼流圈的传递函数为:
$$
G_3 = \frac{1}{L \cdot s + R}
$$
符号含义与第三节III‐A中的相同。如[23]所示,每个逆变器被建模为一个增益$K_i$,并带有时间滞后$T_i$,其中$i = 1,2$:
$$
\begin{cases}
G_{12} = \frac{K_1}{T_1 \cdot s + 1} \
G_{21} = \frac{K_2}{T_2 \cdot s + 1}
\end{cases}
$$
增益可以从直流母线电压$V_{dc}$和最大控制电压$V_{cm}$获得,如下所示:
$$
K_i = 0.65 \frac{V_{dc}}{V_{cm}}
$$
引入系数0.65是为了考虑在给定直流母线电压[23]下逆变器所能获得的最大基波峰值电压。逆变器中的时间滞后等于平均载波开关周期时间,即周期的一半,并用PWM开关频率$f_c$表示为:
$$
T_{1,2} = \frac{1}{2f_{c1,2}}
$$
设$G_{11}$和$G_{22}$分别为两个PI调节器的传递函数,则图19系统闭环传递函数可写成矩阵形式:
$$
I = [W_1(s) - W_2(s)] I_{\text{ref}}
$$
其中:
$$
\begin{cases}
W_1(s) = \frac{G_{11} * G_{12} * G_3}{1 + G_3(G_{12}G_{11} - G_{22}G_{21})} \
W_2(s) = \frac{G_{22} * G_{21} * G_3}{1 + G_3(G_{12}G_{11} - G_{22}G_{21})}
\end{cases}
$$
且
$$
I_{\text{ref}} = [I_{\text{ref1}}, I_{\text{ref2}}]
$$
为了分析系统稳定性范围,根据PI调节器常数的取值,将劳斯‐赫尔维茨判据应用于闭环传递函数$W_1$和$W_2$的分母。在当前情况下,测试逆变器工作在8kHz开关频率,而负载逆变器工作在16kHz开关频率,原因如小节III‐A所述。其余参数见表II。固定两个PI调节器的
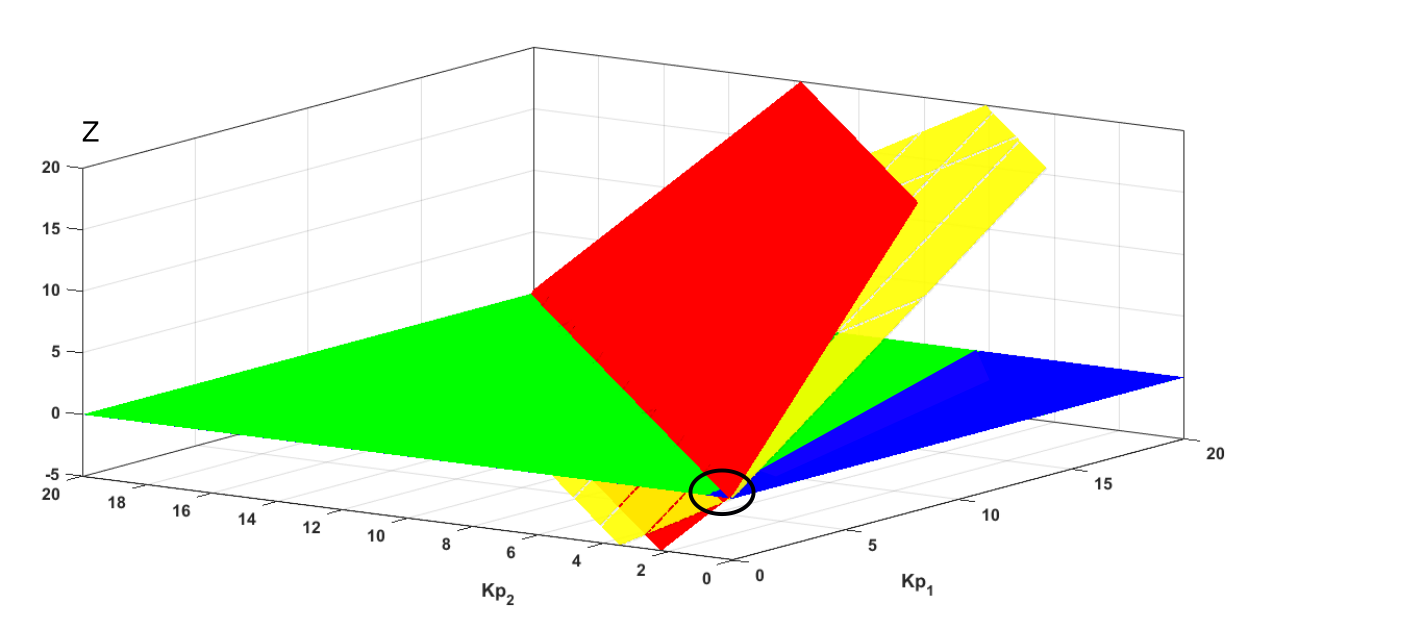
$K_i = 0.6 * K_p$(无论如何,$K_i$可在较宽范围内变化而不影响稳定性),劳斯‐赫尔维茨判据输出矩阵M(见附录),其第一列包含五行,由两个正常数和三个关于$K_{p1}$与$K_{p2}$的函数组成。根据劳斯‐赫尔维茨判据,为实现稳定性,第一列各元素应具有相同符号。由于两个常数为正,需研究第一列中三个函数的符号,从而得到三个关于$K_{p1}$和$K_{p2}$的不等式,表示稳定性条件。这三个不等式可在笛卡尔空间中用三个曲面图形表示。使系统稳定的增益$K_{p1}$和$K_{p2}$的取值是满足这些条件的值。
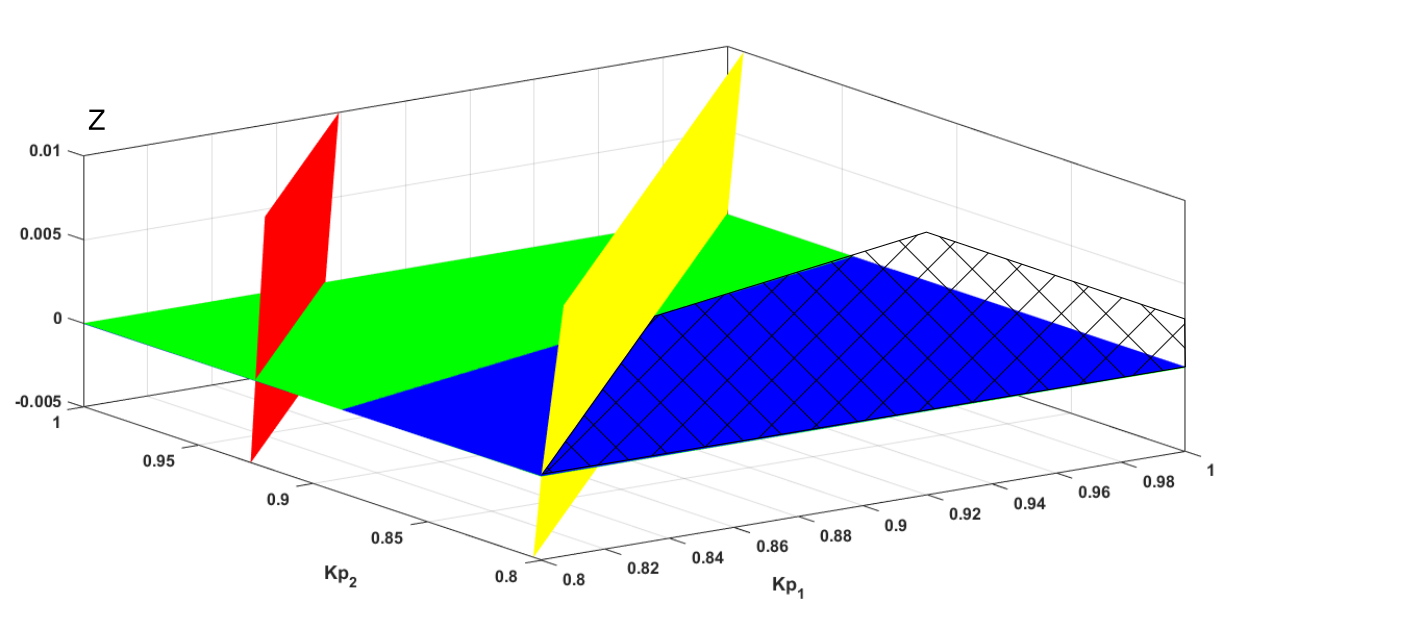
曲面的各点具有正的$z$坐标。这三个曲面如图20所示,其中最显著部分(图20中的圆圈内区域)的放大图如图21所示。绿色曲面表示$z = 0$平面。阴影区域内的点满足全部三个不等式,即如果$K_{p1}$和$K_{p2}$的取值位于该区域内,则系统是稳定的。
为了更清楚地阐明该过程,研究了$K_{p1} = K_{p2}$的稳定性条件。在这种情况下,Routh‐Hurwitz矩阵变为:
$$
\begin{bmatrix}
2.4 \cdot 10^{-12} & 7.5 \cdot 10^{-6} - 2.2 \cdot 10^{-4} \cdot K_p & 0 \
4.4 \cdot 10^{-8} & 0.3 - 1.3 \cdot 10^{-4} \cdot K_p & 0 \
2.1 \cdot 10^{-4} - 2.2 \cdot 10^{-4} \cdot K_p & 0 & 0 \
0.3 - 1.3 \cdot 10^{-4} \cdot K_p & 0 & 0
\end{bmatrix}
$$
对第一列的分析给出了以下稳定性条件:
$$
K_p < 0.9
$$
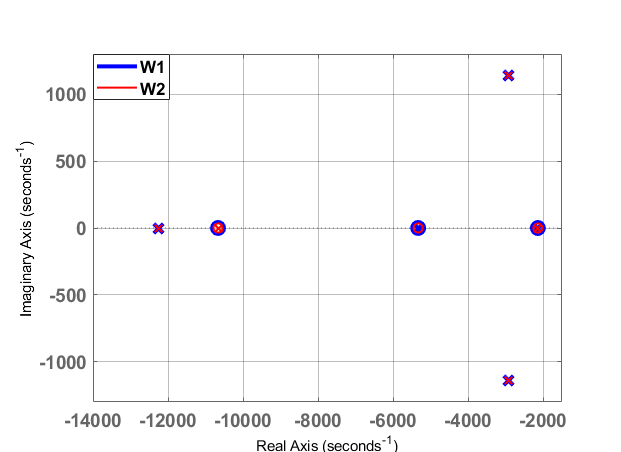
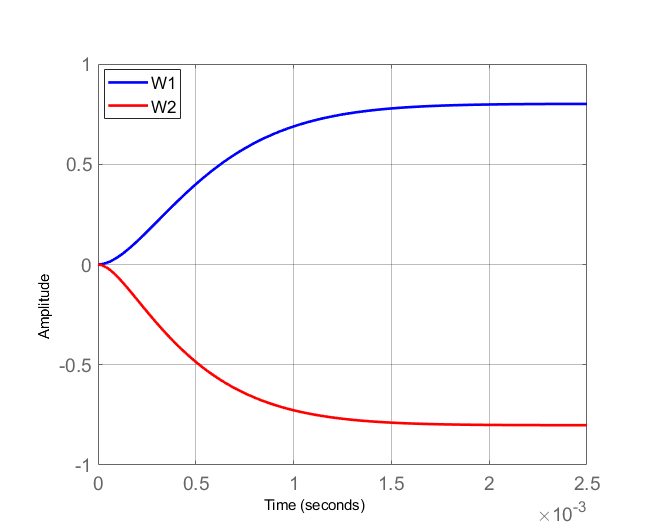
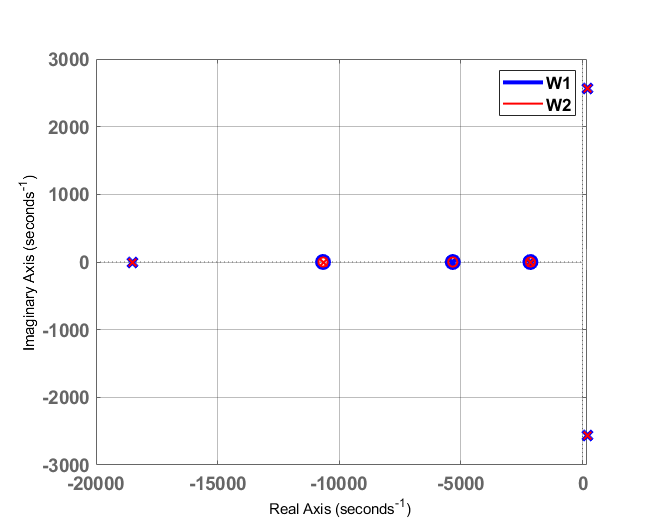
与图21一致。为了验证通过Routh‐Hurwitz判据得到的稳定性条件,图22和图24分别展示了在$K_p = 0.1$和$K_p = 1$情况下,使用表II所示参数的$W_1$和$W_2$的零极点图。
对于$K_p = 0.1$,所有极点都具有负虚部这意味着系统在稳定性方面是稳定的
| 参数 | 值 |
|---|---|
| $K_1, K_2$ | 1.56 |
| $f_{c1}$ | 8 kHz |
| $f_{c2}$ | 16 kHz |
| $L$ | 0.3 mH |
| $R$ | 0.3 Ω |
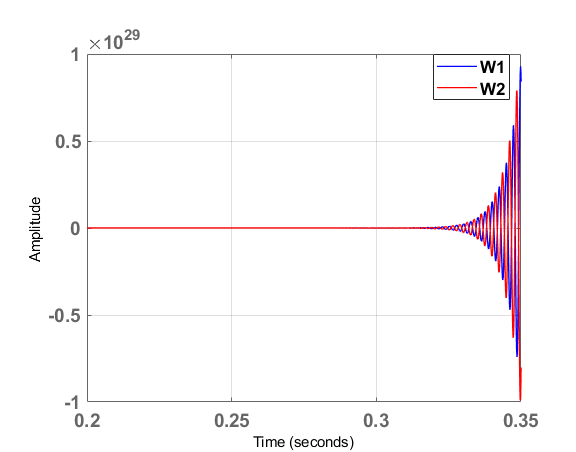
公式39的条件下,而当$K_p = 1$时,会出现两个具有正实部的极点,如图24所示,系统变得不稳定。
阶跃响应常用于模态分析,因为阶跃函数能够激发系统的所有模态。因此,图23显示了$W_1$和$W_2$在$K_p = 0.1$下的阶跃响应。阶跃响应是稳定的,验证了前述的稳定性条件。
阶跃响应也在图25中对$K_p = 1$进行了重复。正如预期的那样,当$K_p$取新值时,系统响应是发散的。
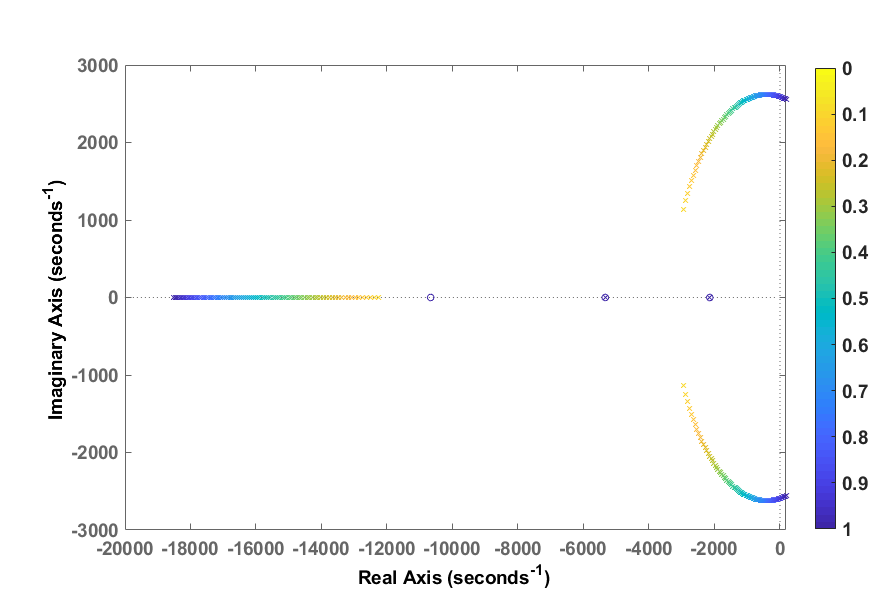
最后,图26显示了通过改变$K_p$得到的极点轨迹。可以看出,增大$K_p$会将极点推向右半平面。
四、测试结果
用于电动汽车的电动驱动系统已通过所提出的技术进行了测试。案例研究A涉及一种包含轴向磁通表面贴装式永磁同步电机的动力总成。该系统为实验室设备,用于验证该概念,以验证电感的选择,并评估正常运行和再生制动时的功率流。案例研究B代表一个用于电动汽车动力总成的全尺寸工业测试台,该动力总成采用内置式永磁同步电机。该测试设备由Loccioni公司建造并安装,旨在使用真实参数对电动汽车的商用驱动器进行测试。案例研究A中车辆和道路的参数见表III,两个案例研究中电机的参数见表IV。
| 表III 两个案例研究的车辆参数 | 值 |
|---|---|
| 车辆质量 | 50 Kg |
| 车轮质量 | 1.5 Kg |
| 车轮半径 | 6 cm |
| 车辆最大迎风面积 | 1.2 m² |
| 表四 两个案例研究的电机参数 | SPM | IPM |
|---|---|---|
| $V_{dc}$ | 24V | 475V |
| $L_d$ | 0.7毫亨 | 0.194毫亨 |
| $L_q$ | 0.7毫亨 | 0.292毫亨 |
| $R_s$ | 0.3Ω | 0.008Ω |
| $p$ | 8 | 4 |
| $\lambda_{pm}$ | 0.01伏秒 | 0.021 |
| $J$ | 0.0035 千克 m² | 0.044 千克 m² |
A. 案例研究A
本节讨论在案例A的实验台上进行不同测试后获得的结果。使用了两台UNITEK DS2420型号的驱动器。为了限制电源功率和扼流圈尺寸,车辆的重量和尺寸均已减小。重量的缩放系数为$s_1 = 0.05$,尺寸的缩放系数为$s_2 = \sqrt[3]{s_1} = 0.37$。所有其他参数均为实际值。这些测试涵盖了以下模拟操作:
• 启动周期;
• 恒定驾驶条件(速度和坡度);
• 恒定速度和可变道路坡度;
• 恒定道路坡度角和可变速度。
上述驾驶循环中牵引电机电枢电流随时间的变化被记录下来。
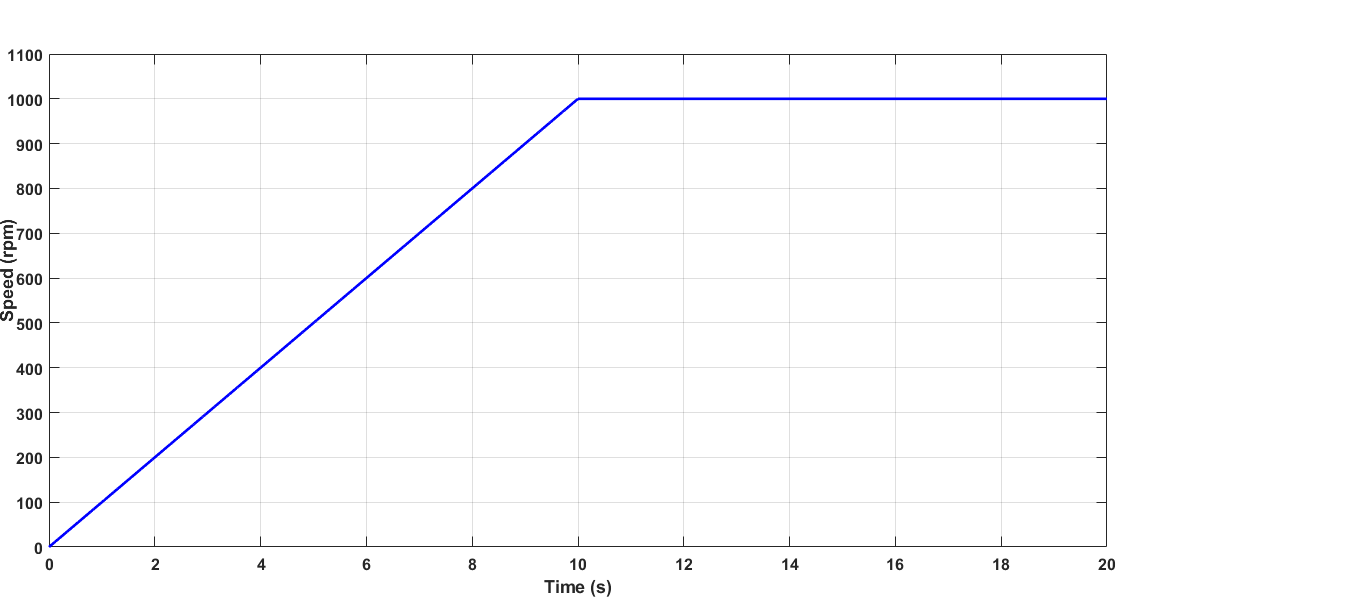
1) 启动
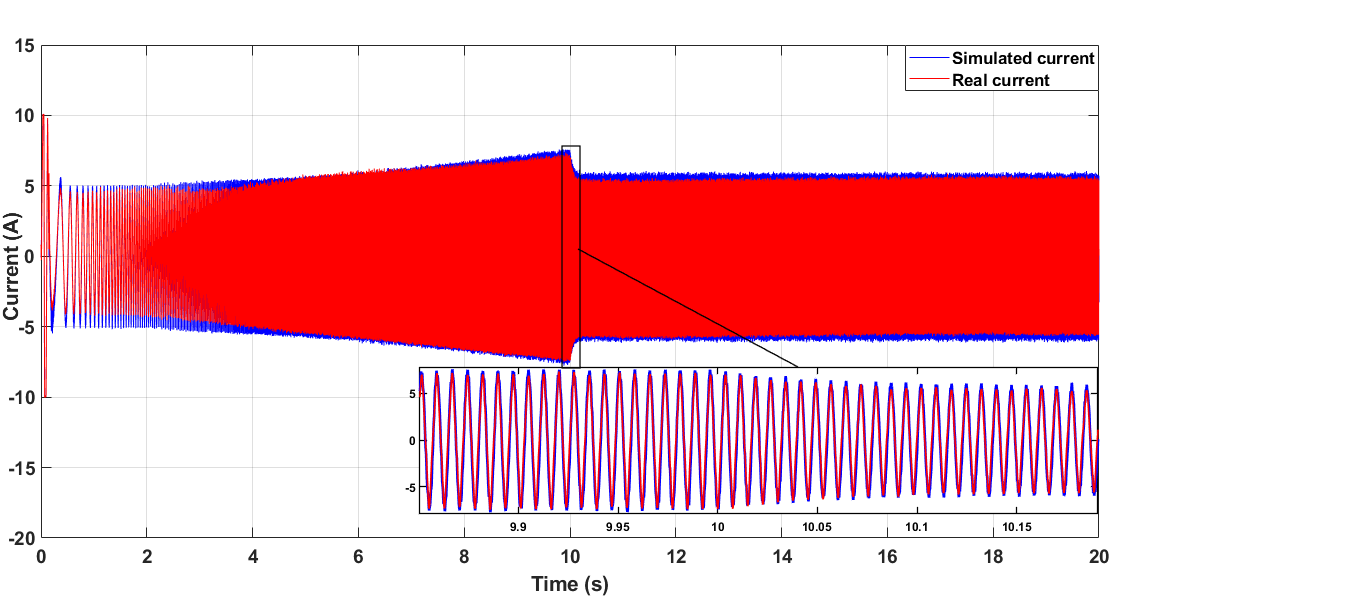
考虑从静止状态到速度参考值等于1000rpm的启动过程,如图27所示。在控制系统嵌入的车辆模型中,道路坡度角保持恒定为零。图28显示了由PXI生成的仿真相电流与在负载逆变器输入端测得的仿真结果的波形。可以看出,在启动期间以及稳态运行时,仿真与仿真结果之间具有相当良好的一致性。
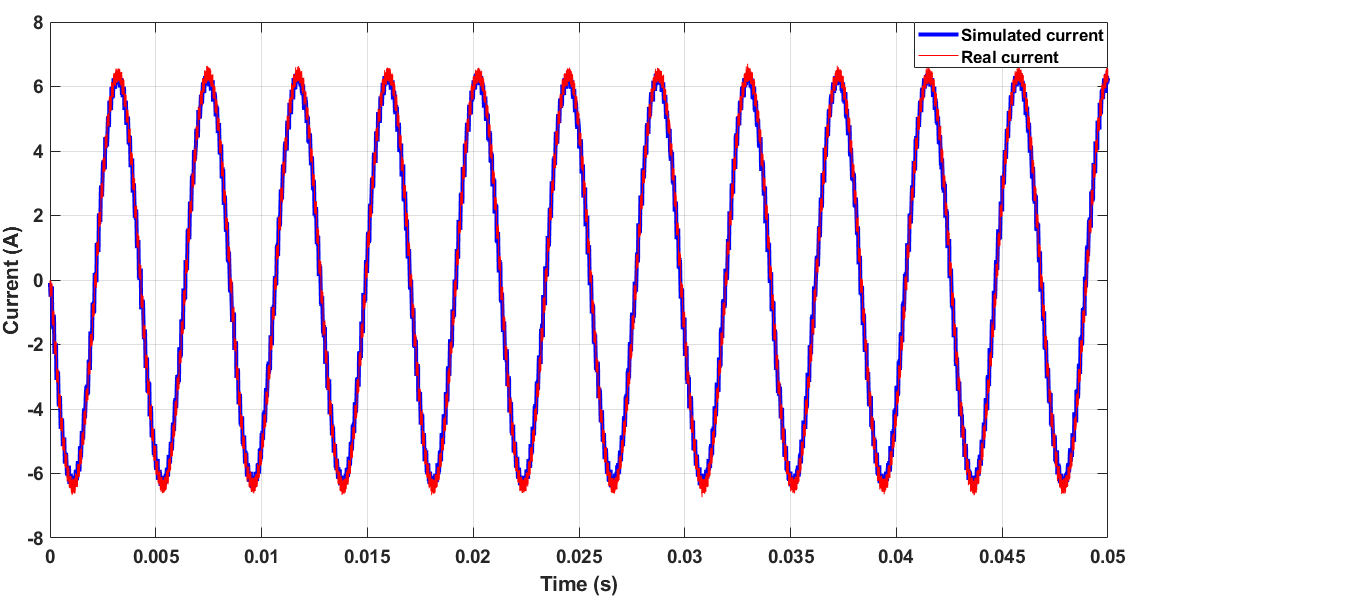
2) 恒定驾驶条件下的运行
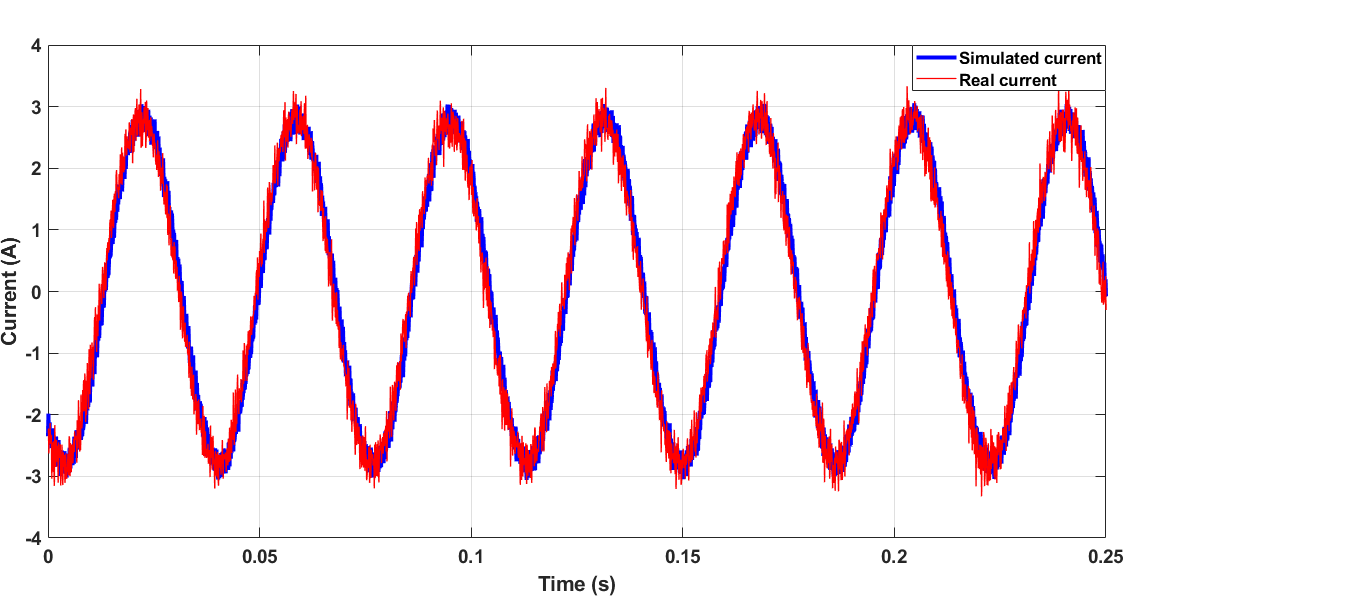
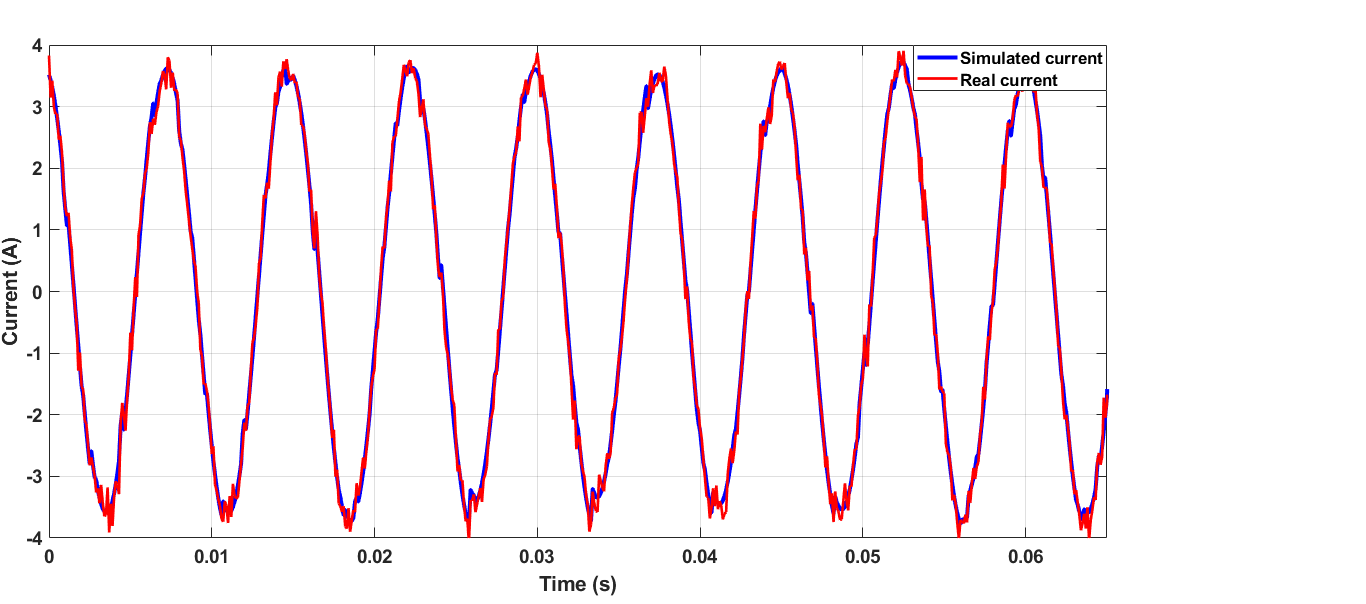
考虑正道路坡度角$0.1$ rad的情况。电动汽车传动系统工作在电动模式。图29.(a)、29.(b)和29.(c)分别显示了速度为200转/分、1000转/分钟和1760转/分钟时的牵引电机相电流。通过分析这些结果,并结合车辆所表现出的负载转矩,可以发现电机相电流随速度非线性地增加。仿真与仿真结果之间具有相当好的一致性。
在仿真和实测波形中,随着速度的增加,电流纹波减小。对于仿真电流,该特性很明显:随着速度增加,反电动势增大,反电动势与电源电压之间的差值减小。此外,电抗增大,因此电流纹波减小。对于实测波形,电流纹波的减小如第III‐B节中分析所述。
3) 恒速变坡道运行
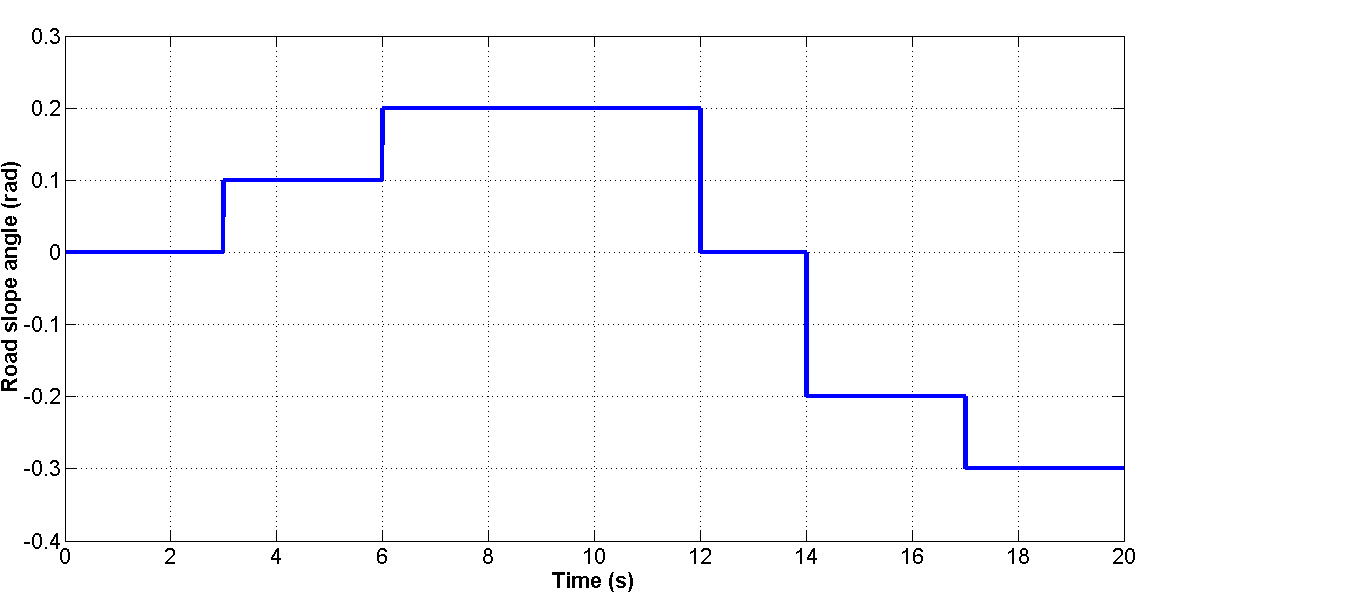
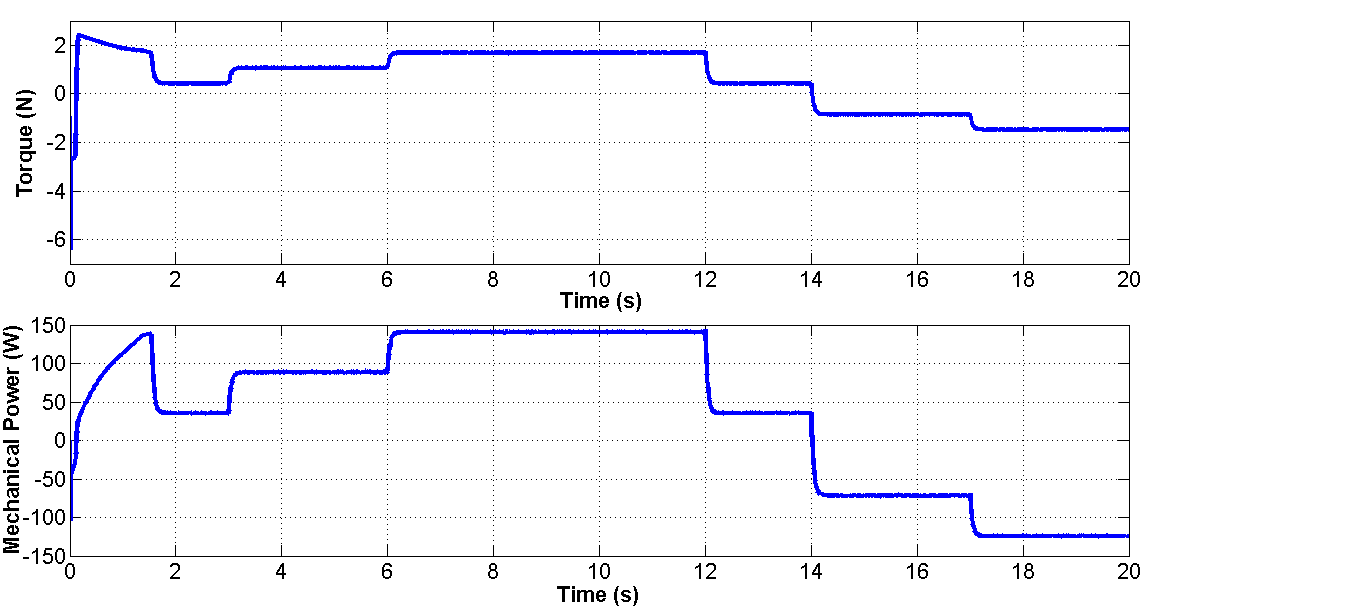
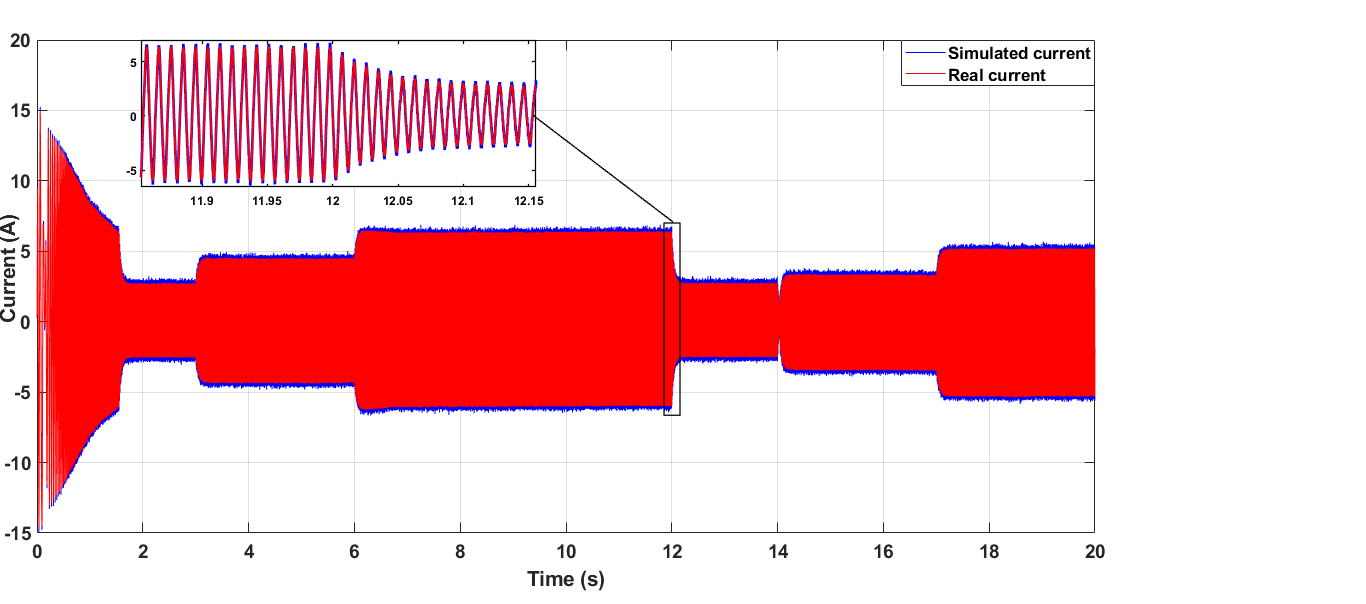
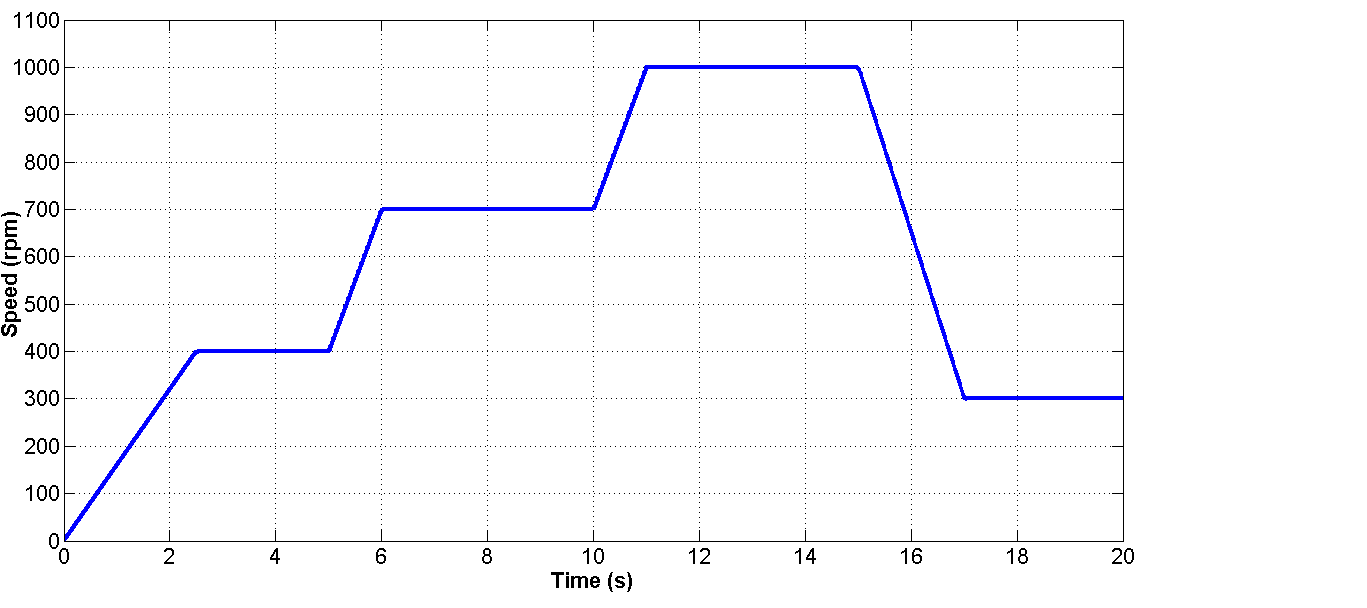
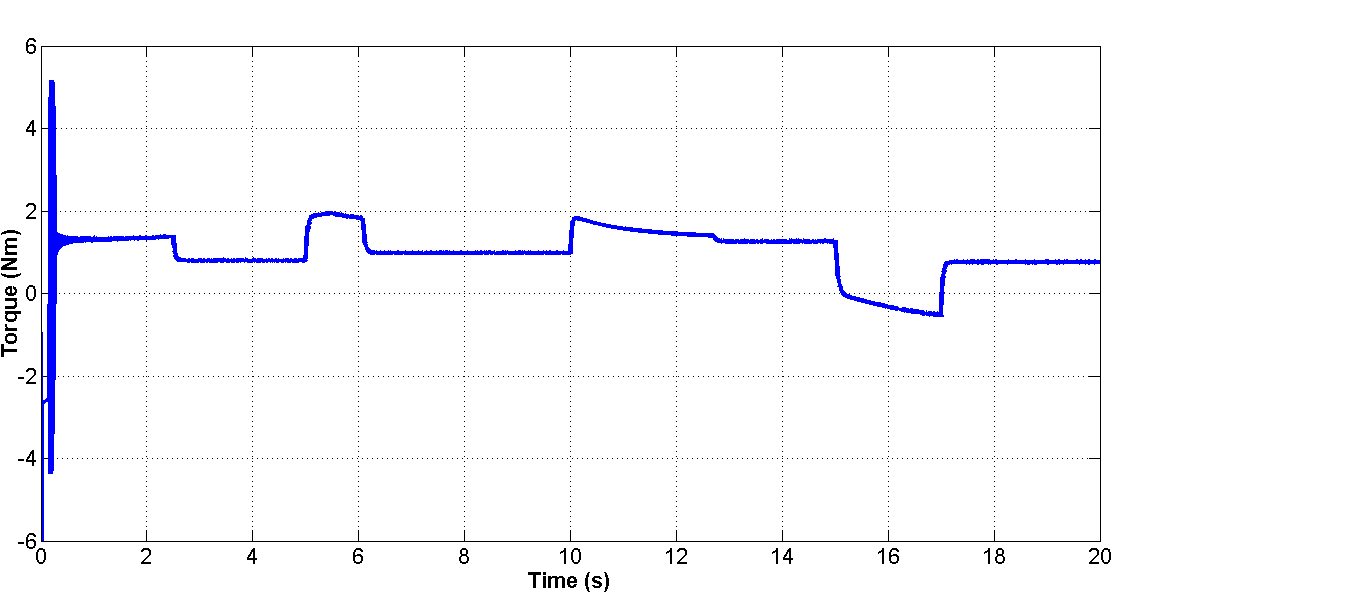
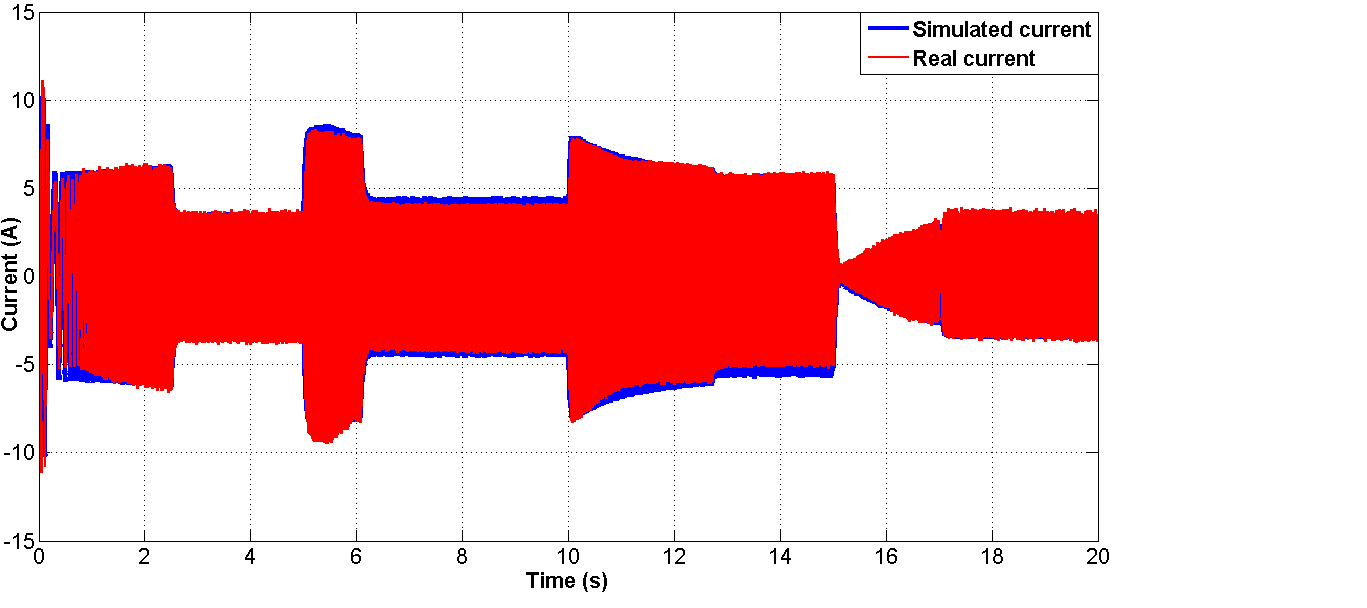
在道路坡度角为零的启动瞬态$\theta = 0$之后,车辆进入稳态运行,其特征是轮速恒定,等于800 rpm,从$t = 1$s开始。在$t = 3$s时,道路坡度按照图30所示周期先正向变化后负向变化。车辆负载转矩和所需机械功率如图31所示。仿真和模拟的PMSM相电流如图32所示。
通过分析这些结果,可以得出以下几点观察:
• 在爬坡期间($\theta > 0$),负载转矩为正,机械功率取正值。该系统
 Nm =200转/分,(b) Nm =1000转/分,(c) Nm =1760转/分)
Nm =200转/分,(b) Nm =1000转/分,(c) Nm =1760转/分)
 )
)
仿真如图2(a)所示的加速驾驶循环,
• 在下坡运行期间($\theta < 0$),负载转矩变为负值,因此机械功率为负值。该系统仿真如图2(b)所示的再生制动周期。
此外,需要注意的是,仿真与模拟的电枢相电流具有良好的一致性,且它们的幅值与图31所示负载转矩的绝对值成正比。
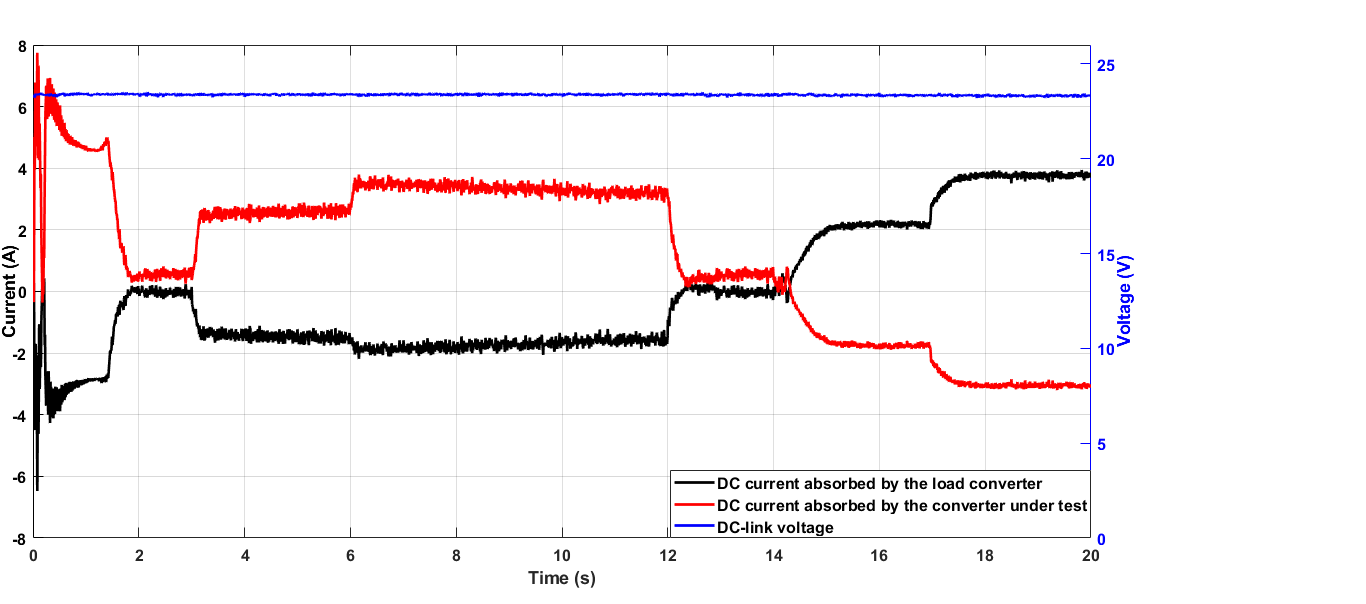
为了深入研究开发的模拟系统的性能,记录了两个变流器输入端的直流电流以及直流电压,并在图33中显示。从对图33的分析可以看出:
• 为正坡度时(大致表示系统施加正转矩),被测变流器作为逆变器运行,其输入端的直流母线电流为正,而负载变流器则作为整流器运行,具有负的直流母线电流。此场景仿真图2(a)所示的加速周期;对于负坡度(从$t = 14$s开始),被测变流器作为整流器运行,具有负直流母线电流,而负载变流器作为逆变器运行,具有正直流母线电流。该场景仿真了图2(b)所示的再生周期;
• 在两个阶段中,系统中的功率损耗导致直流电流幅值的差异。为了说明最后的考虑,可以计算功率平衡。系统在电动模式下的功率平衡可表示为:
$$
P_{in} = P_{losses} + P_{out}
$$
其中
• $P_{in}$是来自测试逆变器直流链路的输入功率;
• $P_{loss}$是测试系统中的总功率损耗;
• $P_{out}$是从负载逆变器回馈到直流母线的输出功率。
例如,在图19中$t = 4$s处,输入功率计算为:
$$
P_{in} = I_{in} V_{dc} = 2.5 * 24 = 60W
$$
其中$I_{in}$是直流电流的瞬时值,$V_{dc}$是直流母线电压。
系统中的总功率损耗$P_{loss}$主要消耗在两个变流器和电感中。其计算方法如下:
$$
P_{loss} = P_{conv1} + P_i + P_{conv2}
$$
其中$P_{conv1}$和$P_{conv2}$分别是第一个和第二个逆变器中的损耗(导通损耗与开关损耗之和),$P_i$是电感中的损耗。
电感中的功率损耗由电感铜线和铁芯中的焦耳损耗引起。铜线电阻$R_i$和铁芯等效电阻$R_\mu$已通过实验测定。其数值为:
$$
\begin{cases}
R_i = 0.3\Omega \
R_\mu = 4.58\Omega
\end{cases}
$$
设$I_i$为图18所示电感中交流相电流的有效值,$I_a$为电感电流的有功分量,则三相电感中的功率损耗为:
$$
P_i = 3
(R_i I_i^2 + R_\mu I_a^2) = 3[0.3
(3.18)^2 + 4.58*0.7^2] = 15.8W
$$
$P_i$的测量值与公式44中计算的值一致。
两个逆变器中的损耗已进行测量,其数值为:
$$
\begin{cases}
P_{conv1} = 4.2W \
P_{conv2} = 4.7W
\end{cases}
$$
根据公式42,系统中的总功率损耗为$P_{loss} = 24.773W$。
由公式40可计算输出功率如下:
$$
P_{out} = P_{in} - P_{loss} = 35.2W
$$
输出功率可以表示为输出电流$I_{out}$与直流母线电压的乘积,如下所示:
$$
P_{out} = I_{out} V_{dc}
$$
最后,输出电流可以计算为:
$$
I_{out} = P_{out}/V_{dc} = 1.46A
$$
该值与图33中的值一致。
在再生模式下,即从$t = 14$s开始,会产生反向功率流。在图33中,由于速度和转矩的值不同,直流电流与$t = 4$s时不同,因此损耗的值也不同。
4) 恒定道路坡度和可变速度下的运行
让我们考虑车辆在以下条件下运行的情况:
• 恒定道路坡度角$\theta = +0.1$rad,

• 一个速度循环,包括一次启动、两次加速和一次减速,如图34所示。
车辆模型产生的仿真负载转矩如图35所示。相应的仿真与模拟的电枢相电流如图36所示。
从这些结果的分析可以看出,在减速过程中,负载转矩减小并达到负值。这为再生模式提供了可能,即将动能转化为电能,并储存在电动或混合动力车辆的电池中。
B. 案例研究B(ECE城市驾驶循环)
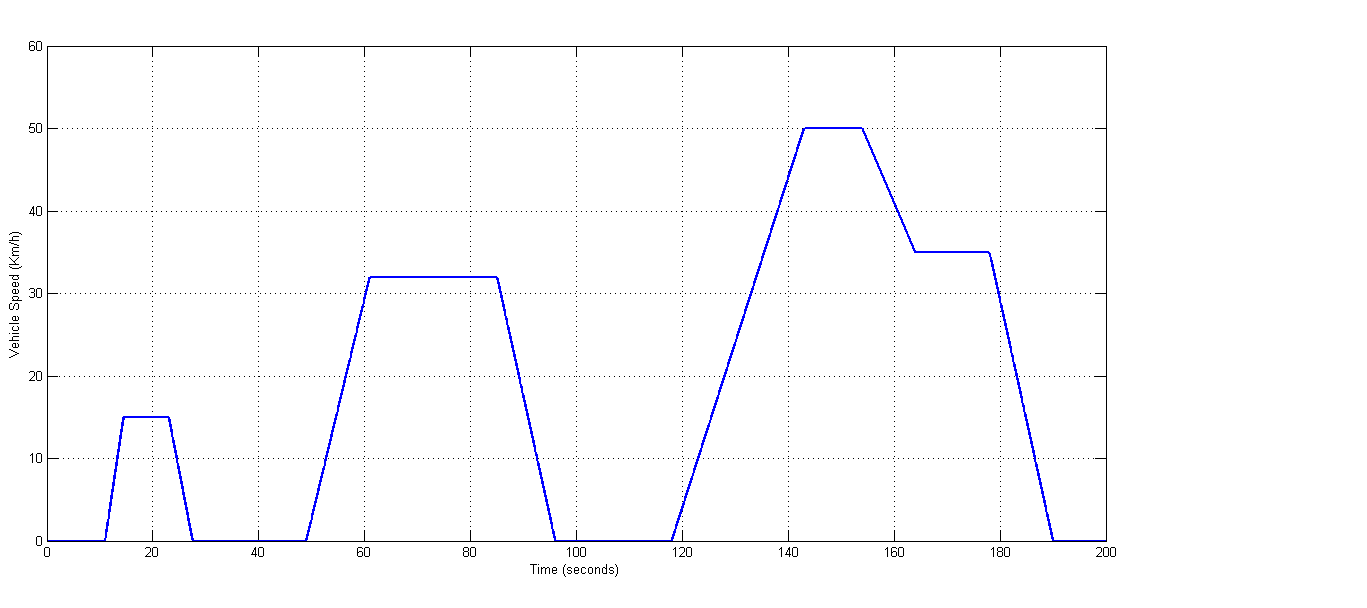
在案例研究B中,全尺寸模拟器被用于测试商用驱动器。负载驱动器为定制驱动器。图37所示的ECE为市区驾驶循环(Urban Driving Cycle),简称UDC,旨在代表典型的城市驾驶工况。该ECE持续时间为195s,预计行驶距离约为994.03 m,最高速度为50 km/h。该循环的设计目的是限制尾气排放。
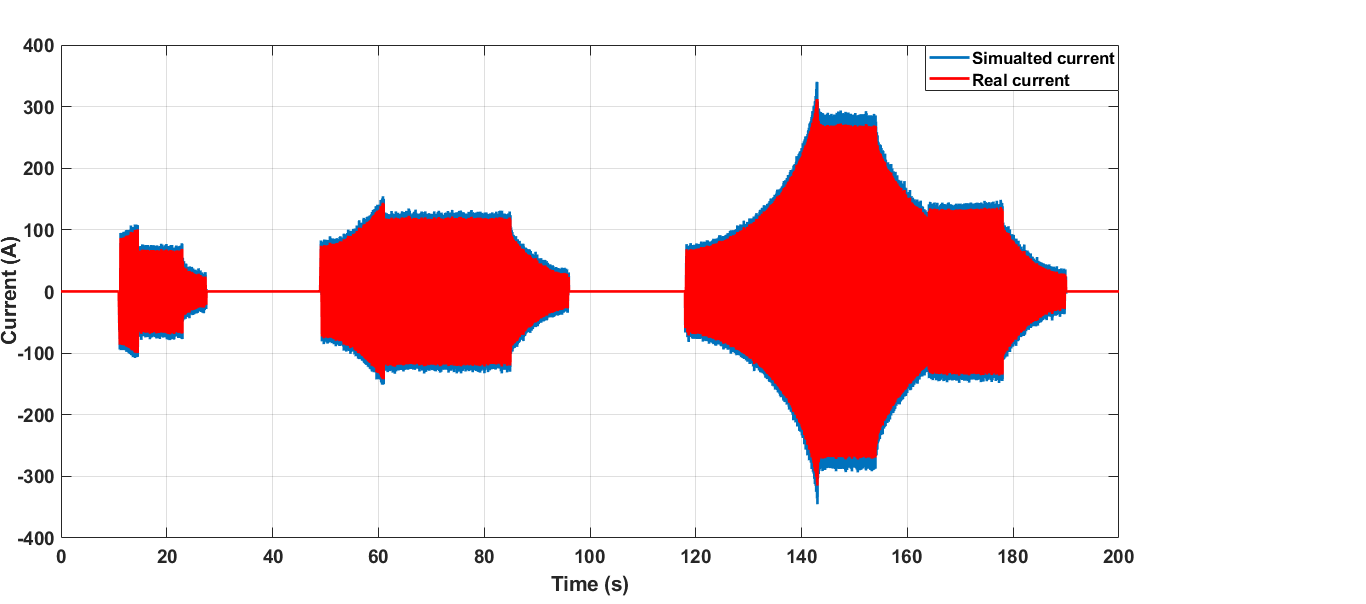
系统的响应如图38所示,其中比较了仿真和仿真的电流。与之前的情况一样,该系统能够正确地模拟内置式永磁电机驱动器的特性。通过使用标准化的驾驶循环,在虚拟环境中再现电动汽车的实际驾驶工况,从而验证了测试台。在制动阶段,能量回收得以正确实现。
五、结论
本文介绍了用于汽车电驱动系统测试的装置开发及其实验验证。该系统由:
• 待测试的电动动力总成;
• 作为负载的电驱动器,其交流侧通过三相扼流圈与被测驱动器相连。负载驱动器仿真牵引电机驱动电动汽车车轮的过程;
• 在NI PXI实时仿真硬件在环系统中实现的控制系统。
该控制系统在实时环境中对三个模型的方程进行积分:– 内置式永磁(或表面贴装磁铁)同步电机;–矢量控制;–车辆动力学。
在NI PXI接口中实现的仿真程序考虑了由矢量控制的电压源逆变器供电的永磁同步电机(PMSM)。PMSM机械方程中所考虑的负载转矩由车辆动力学模型提供。实时实现能够在0.1ms的采样时间内完成所有控制任务。
对电流纹波的分析表明,纹波与扼流圈参数和速度相关。扼流圈的取值已选择为在不引入过大电流变化延迟的情况下使纹波最小化。通过分析电力系统组件的传递函数,验证了系统的稳定性。并通过PI调节器的比例增益评估了稳定范围。
实验部分展示了在所开发平台上进行的不同测试的结果。为了验证所提出的设置,模拟了不同的城市驾驶循环。作为概念验证,两项案例研究已在实验室环境中实施,并在工业全尺寸测试设施上进行了实现。在这两种情况下,仿真与模拟结果之间均表现出高度一致性。此外,还重点讨论了所开发平台展现的再生制动能力。
所提出的平台具有用于构建电机模拟器的硬件简单的特点,这使得测试系统基于其成本效益、高性能和功耗而在工业应用中具有适用性。




















 410
410

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








