高频低剖面可弯曲转换器设计

分析与设计一种用于可弯曲设备的高频低剖面转换器

摘要

本文提出了一种基于空芯电感器的用于可弯曲设备的10MHz低剖面转换器。分析了在不同弯曲情况下可弯曲平面圆形螺旋线圈的数学模型和电感计算方法。详细描述了一种T型匹配网络的优化设计方法，该方法通过实现弱感性等效输入阻抗，确保在整个弯曲范围内具有软开关特性和高效率。在实验室中提出了一款32V输入、9V/6.3W输出的原型，实验结果验证了所提出的优化设计方法的可行性，系统效率相比传统方法可提高4%。

Index Terms— 高频变换器，可弯曲平面线圈，软开关特性，匹配网络。

一. 引言

随着材料技术的发展，越来越多的可弯曲产品（如显示器、太阳能电池和照明应用）逐渐出现在消费电子市场中。与刚性系统相比，它们更轻便且可弯曲，更适合可穿戴或便携式设备 [1‐3]。

为了形成可弯曲系统，这些设备的电源也需具备可弯曲特性，其中，电感器占据了功率转换器的最大体积，因此其弯曲特性受到了广泛关注。在[4]中提出了一种基于同轴电缆材料的可弯曲电感的升压转换器。通过提高频率，可在每个开关周期内减少无源元件的能量存储，从而降低无源元件的值。当频率增加至数十兆赫兹时，系统的功率密度得以提升，并可采用平面空芯螺旋线圈来帮助降低系统的垂直高度，进而形成平面转换器[5‐7]。

当这些平面结构用于可弯曲功率变换器时，线圈绕组可以印刷在聚酰亚胺或聚酯薄膜等可弯曲基板上以匹配系统的可弯曲性。一些可弯曲功率变换器中采用了方形螺旋线圈，包括降压型、LLC 和无线电力传输系统的耦合线圈。通过数值计算、仿真和测量研究了线圈在不同弯曲角度下的电感变化 [8‐13]。然而，对于具有更高品质因数的平面圆形线圈，目前尚缺乏足够的分析。

值得注意的是，由于平面线圈的电感在不同的弯曲程度下会发生变化，系统将偏离最佳工作点。这种现象可能导致一系列问题，例如软开关特性丢失、输出电压和电流变化。尽管[12‐15]中的设计讨论了弯曲程度对线圈电感的影响，但并未对该影响进行设计上的干预，因此系统在不同弯曲角度下的性能会发生剧烈变化。

高频（HF）和甚高频（VHF）功率变换器通常由三部分组成：逆变级、匹配网络和整流级。匹配网络是连接逆变级和整流级的桥梁，用于调节阻抗以提高逆变器的功率和效率。对于工作在数兆赫至数十兆赫频率级别的逆变级，D类拓扑具有最低的电压应力，并且仅需感性负载即可实现软开关。当匹配网络的阻抗呈弱感性时，开关的体二极管可在死区期间避免导通，从而进一步降低逆变器的损耗[16‐17]。因此，有必要通过优化参数设计研究如何抑制电感变化对匹配网络输入阻抗角的影响。目前关于匹配网络的设计研究一直集中在消除负载变化的影响上。[18‐19]为宽负载变化范围设计了纯电阻型T型/ π型匹配网络，而[20]设计了 π型匹配网络以消除无线电力传输中互感的变化。在[21‐22]中，采用可调电容器设计匹配网络，并通过调节电容值来确保系统在不同负载下性能保持不变。上述现有研究均遵循在负载变化条件下设计网络参数的原则，而很少提及阻抗网络自身参数偏差的影响。

本文基于对一种可弯曲转换器的分析，第二节分析了可弯曲平面空心电感器的电感计算方法，第三节设计了在可弯曲电感条件下的T型匹配网络。第四节和第五节分别为实验结果和结论。

II. 可弯曲平面空心电感器分析

圆形螺旋线圈的内径为 $R_1$，外径为 $R_N$，匝数为 $N$。线宽为 $w$，线间距为 $d$，铜厚为 $\delta$。当线圈沿 $x$ 轴弯曲角度 $\theta$ 时，线圈在 $xy$ 平面上的投影如图1所示。

为了便于分析，如图1所示，沿x轴将线圈分为两部分。在$x > 0$区域内的第i匝导体表示为$i+$，在$x < 0$区域内的第i匝导体表示为$i-$。然后，各导体段的坐标可表示为：

$$
\begin{cases}
(x_i, y_i, z_i) = \left(A_i, y, \sqrt{B_i^2 - y^2}\right), & y \in [-B_i, B_i] \
(x_i, y_i, z_i) = \left(-A_i, y, \sqrt{B_i^2 - y^2}\right), & y \in [-B_i, B_i]
\end{cases}
$$

and among them,

$$
\begin{cases}
A_i = \frac{R_N}{\sin(\theta/2)} \
M = \frac{R_N}{\theta} \
B_i = R_i
\end{cases}
$$

根据(1)，可得到坐标的偏导数为：

$$
\begin{cases}
\frac{\partial(x_i, y_i, z_i)}{\partial y} = \left(0, 1, \frac{-y}{\sqrt{B_i^2 - y^2}}\right), & y \in [-B_i, B_i] \
\frac{\partial(x_i, y_i, z_i)}{\partial y} = \left(0, 1, \frac{-y}{\sqrt{B_i^2 - y^2}}\right), & y \in [-B_i, B_i]
\end{cases}
$$

计算电感的方法根据诺伊曼公式和罗莎方程计算电感 [13]。

$$
L =
\begin{cases}
\sum_{i=1}^{N}\sum_{j=1}^{N} \frac{\mu_0}{4\pi} \int \int \frac{dl_i \cdot dl_j}{|r_i - r_j|}, & i \neq j \
\sum_{i=1}^{N} \left[\frac{\mu_0 l_i}{2\pi} \left(\log\left(\frac{2l_i}{w + \delta}\right) + 0.5\right)\right], & i = j
\end{cases}
$$

将(1)和(3)代入(4)，可从(5)推导出第i根与第j根导体之间的互感：

$$
L(i,j) =
\begin{cases}
\frac{\mu_0}{4\pi} \int_{-B_j}^{B_j} \int_{-B_i}^{B_i} f_1(y_1,y_2) dy_1 dy_2, & i \neq j \
\frac{\mu_0}{4\pi} \int_{-B_j}^{B_j} \int_{-B_i}^{B_i} f_2(y_1,y_2) dy_1 dy_2, & i = j
\end{cases}
$$

where the expressions of $f_1(y_1,y_2)$ and $f_2(y_1,y_2)$ are as shown in (6)。

$$
f_1(y_1,y_2) = \frac{(A_iA_j + y_1y_2)(B_i^2 - y_1^2)^{1/2}(B_j^2 - y_2^2)^{1/2}}{[(A_i - A_j)^2 + (y_1 - y_2)^2 + ((B_i^2 - y_1^2)^{1/2} - (B_j^2 - y_2^2)^{1/2})^2]^{3/2}}
$$

$$
f_2(y_1,y_2) = \frac{(A_iA_j + y_1y_2)(B_i^2 - y_1^2)^{1/2}(B_j^2 - y_2^2)^{1/2}}{[(A_i - A_j)^2 + (y_1 - y_2)^2 + ((B_i^2 - y_1^2)^{1/2} - (B_j^2 - y_2^2)^{1/2})^2]^{3/2}}
$$

Then the self-inductance of the N-turns coils can be solved as follows:

$$
L_{coil} = \sum_{i=1}^{N} \sum_{j=1}^{N} [L(i+,j+) + L(i+,j-)]
$$

根据上述分析与推导，圆形线圈的电感计算程序可设计为图2所示的流程图。为了加快计算速度，可将线圈等效为多个直线导体段，从而将(5)中的积分运算替换为累加运算。

根据上述分析与推导，计算了不同匝数和弯曲角度下的线圈电感。由于电感值是通过将圆形线圈分割为多个导体而得到的，如图2所示，在较大的线圈尺寸下建议使用更大的“Segments”。在不同线圈尺寸下的计算与测量结果如图3所示，两者吻合良好。各线圈的计算与测量误差以及所选的计算步骤见表I。所有电感值均在10MHz频率下使用KEYSIGHT E4990A测量得到。当线圈从0度弯曲到180度时，电感减小约13%。当线圈非对称弯曲时，也可采用附录中所示的分析方法。

表I 电感计算的步长和误差

匝数	段数	θ= 0度	θ= 45°	θ= 90°	θ= 135°	θ= 180°
N=6	50	3.98%	3.95%	2.91%	0.98%	2.84%
N=8	50	3.68%	4.39%	5.03%	0.61%	1.01%
N=10	80	2.94%	2.84%	2.25%	3.30%	7.43%
N=12	100	4.29%	3.92%	1.37%	1.29%	4.99%

III. 匹配网络的分析

高频直流/直流转换器通常由一个逆变器、一个匹配网络和一个整流器组成。对于可弯曲直流/直流转换器而言，最重要的任务是消除电感变化对匹配网络的影响，这主要体现在阻抗角上。所提出的转换器的电路图以及电流和电压波形如图4和图5所示。

根据基尔霍夫电压和电流定律以及傅里叶变换，匹配网络的电压和电流可由(8)推导得出：

$$
\begin{cases}
u_{INV} = i_{INV} \cdot jX_1 + jX_2 \cdot (i_{INV} - i_{REC}) \
u_{REC} = i_{REC} \cdot jX_{bent} + jX_2 \cdot (i_{REC} - i_{INV}) + i_{REC} \cdot R_{REC} \
u_{REC} = i_{REC} \cdot R_L
\end{cases}
$$

然后，整流器的电压比、阻抗角和等效阻抗 $R_{REC}$ 可从 (9) 式得到：

$$
\begin{cases}
G = \frac{u_{REC}}{u_{INV}} = \frac{X_1 R_{REC}}{X_1 X_2 + X_1 X_{bent} + X_2 X_{bent} + X_2 R_{REC}} \
\varphi_{INV} = \tan^{-1}\left(\frac{X_1 X_2 + X_1 X_{bent} + X_2 X_{bent} + X_2 R_{REC}}{X_1 R_{REC}}\right) \
R_{L} = \frac{4}{\pi^2} R_{REC}
\end{cases}
$$

为了研究 $X_1$, $X_2$, 和 $X_{coil}$ 的设计方案，引入了中间变量 $m$ 和 $k$。$k$ 为电感变化比，可表示为 $L_{bent} = kL_{coil}$，其中 $L_{coil}$ 和 $X_{coil}$ 分别为线圈电感和阻抗在 $\theta= 0$ 度，$L_{coil}= j\omega X_{coil}$；$L_{bent}$ 和 $X_{bent}$ 是其他弯曲角度下的电感和阻抗，$L_{bent}=j\omega X_{bent}$。$m$ 是 $X_2$ 和 $X_{coil}$ 的比值。则 $X_2$, $X_{bent}$ 可表示为：

$$
\begin{cases}
X_2 = mX_{coil} \
X_{bent} = kX_{coil}
\end{cases}
$$

如上述分析所述，当线圈弯曲到一定角度时，其电感会相应减小，从而导致 $k$ 下降。通过在阻抗角 $\varphi_{INV}$ 的 $k_{min}$ 和 $k_{max}$ 处设置两个零点，$\varphi_{INV}$ 将随着 $k$ 先上升后下降，从而限制 $\varphi_{INV}$ 的变化范围。当零点未设置在 $k_{min}$ 时，$\varphi_{INV}$ 将始终上升或下降，导致较大的 $\Delta \varphi_{INV}$。

此外，匹配网络的电压增益为 $G= u_{INV}/u_{REC}$。根据图5中的波形，可计算得 $u_{INV}= 2 V_{IN}/\pi$，$u_{REC}= 2 V_O/\pi$。然后由上述分析可知，匹配网络的三个约束条件可由 (11) 得出。

$$
\begin{cases}
G = V_O / V_{IN} \
\varphi_{INV}| {k=k {max}} = 0 \
\varphi_{INV}| {k=k {min}} = 0
\end{cases}
$$

实际上，阻抗应略大于零。然而，为了建立用于计算参数的相应方程，将阻抗角设为零。在实际构建原型时，可以通过微调电感和电容值使阻抗略微呈电感性。

将(10)代入(8)和(9)，根据指定的输入输出参数 $V_O$、$V_{IN}$、$R_{REC}$ 和 $k_{min}$，可由(12)计算出中间变量 $m$。

$$
m = \frac{3k_{min}^2 + 3k_{min}G - 8G^2 + 1 - G^2/k_{min}}{4k_{min}^2 + 3k_{min}G - 3G^2}
$$

Taking one situation as an example, Fig. 6 shows 在不同 $m$ 值下 $\varphi_{INV}$ 的变化，图7是基于图6的 $\Delta \varphi_{INV}$ 与 $m$ 之间的关系。

下一步，$X_{coil}$，$X_2$，$X_1$ 可以从 $m$ (13) 根据 $m$。

$$
\begin{cases}
X_{coil} = R_{REC} \left(\frac{V_O}{V_{IN}}\right) \left(m - \frac{V_O}{V_{IN}}\right), & 1 < m < 1.5 \
X_2 = \frac{R_{REC}}{m} \left(\frac{V_O}{V_{IN}}\right) \left(1 - \frac{V_O}{V_{IN}}\right), & m > 1 \
X_1 = \frac{R_{REC}}{(1 - m)\left(\frac{V_O}{V_{IN}}\right)} \left[\left(1 - \frac{V_O}{V_{IN}}\right)^2 - m\left(\frac{V_O}{V_{IN}}\right)^2\right], & m < 1
\end{cases}
$$

图8所示的框图。

IV. 实验结果

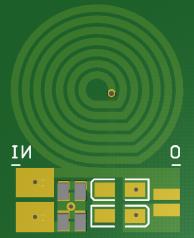
基于提出的设计方法，构建了一个10MHz, 9V/6.3W且输入电压为32V的原型，用于验证上述设计方法的可行性和正确性。具体的电路参数如表二所示。

表II 原型的实验参数

标签	值
C1	821皮法 700安 821千瓦（ATC）
C2	1362皮法 700安 681千瓦（ATC）*2
Cin	10uF GRM21BR61H106KE43L（村田）
Co	10uF GRM21BR61H106KE43L（村田）
Lcoil	120纳亨 电阻7=11mm w=1mm d=0.5mm N=7 δ=1盎司
D1, D2	BAS3010B（英飞凌）
S1, S2	EPC2001C（EPC）
Load	LL159FR1（LG）

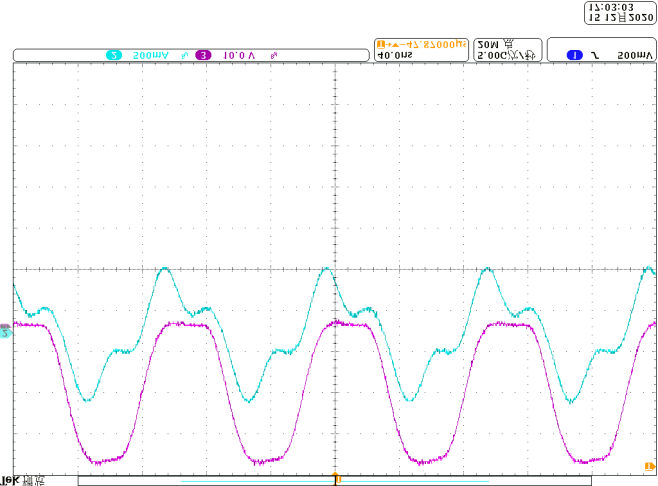
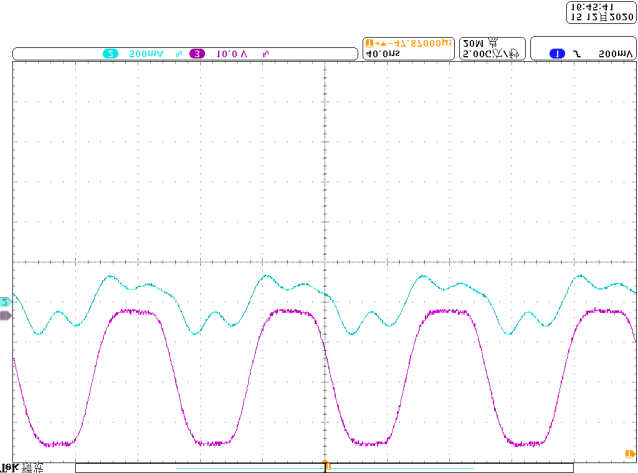
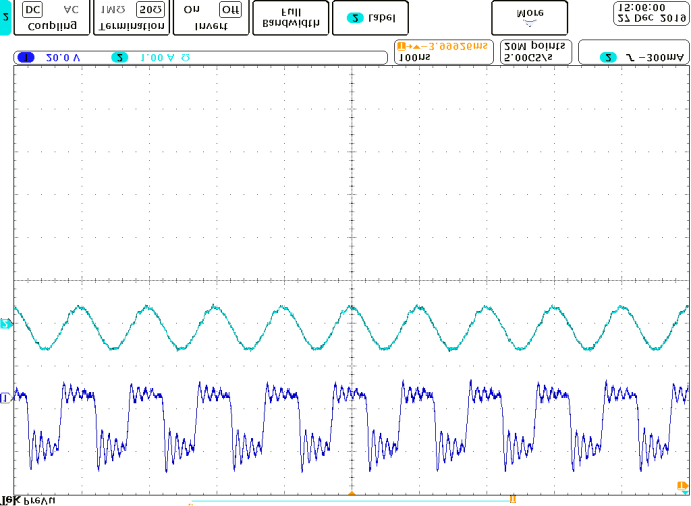
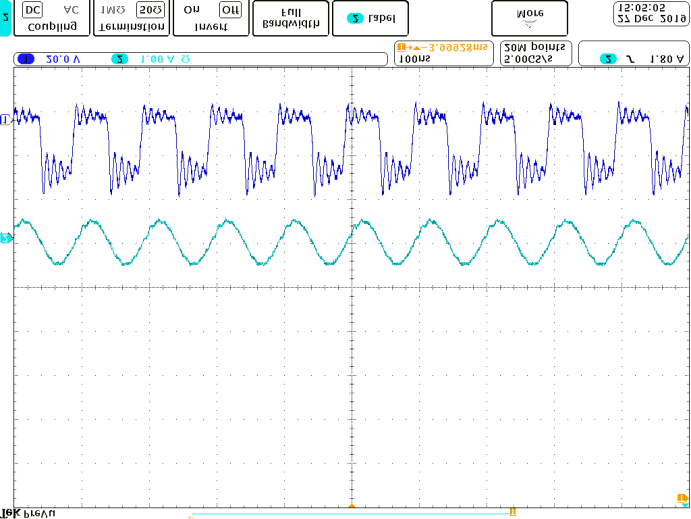
使用安捷伦DSO7104A测量电压和电流，原型的电源为RIGOL DP832。在不同线圈弯曲角度下，图14显示了匹配网络输入电压 $u_{INV}$ 和电流 $i_{INV}$ 的波形。在0°和180°的弯曲情况下，谐振电流与电压同相，有助于开关实现软开关。图15显示了输出电压 $V_O$。当变换器和空芯电感器弯曲时，输出电压没有显著变化，输出电压的最大偏差约为25%。如果期望输出电压被限制在较窄范围内，则必须对弯曲角度加以限制。在当前研究中，输入阻抗角是主要关注点。在未来的工作中，将进行多目标优化。将分析优化算法，以进一步提升所提出系统的性能，同时优化相位角和输出电压。

在软开关状态下，基于GaN的逆变器的主要损耗是 S1和S2的电容损耗和二极管导通损耗，可表示为：

$$
P_C = \frac{1}{2} V_{IN}^2 C_{DS} f_s
$$

$$
P_S = \frac{V_{S-D} I_{IN}}{\pi} \left[ \cos(\varphi_{INV}) - \cos(\omega t_2 + \varphi_{INV}) \right]
$$

其中 $C_{DS}$ switch, $V_{S-D}$ 为体二极管导通电压，$t_2$ 为电容充电结束时间，可通过 (17) 计算：

$$
t_2 = \frac{1}{f_s} \left[ \arccos\left( \frac{V_{IN}}{V_{IN}} \right) + \frac{\pi}{2} + \varphi_{INV} \right]
$$

匹配网络的主要损耗来自线圈电阻，其可表示如下：

$$
P_{coil} = \int (i_{INV} - i_{REC})^2 R_{coil} dt
$$

损耗包括二极管导通损耗，如公式(19)所示，其中 $V_D$ 是二极管正向导通电压。

$$
P_D = V_D I_O
$$

在不同弯曲角度下，各组件的计算损耗如图16所示。由于所提出的拓扑结构能够抑制阻抗角的变化，当线圈弯曲时，逆变器 $P_{S1} + P_{S2}$ 的损耗保持相对稳定。另一方面，电感损耗 $P_{L-bent}$ 和二极管损耗 $P_{D1} + P_{D2}$ 随着弯曲而增加，这是因为在弯曲过程中线圈电感减小，进一步增加了匹配网络增益 $G(u_{REC} /u_{INV})$，导致线圈电流 $i_{coil}$ 增大。

不同弯曲角度下的效率如图17所示。与传统设计方法相比，由于维持了电阻输入阻抗和实现了软开关，系统的整体效率更高且更稳定。

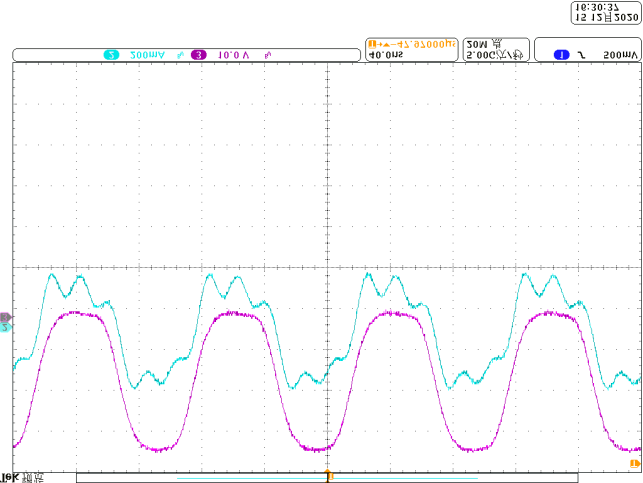
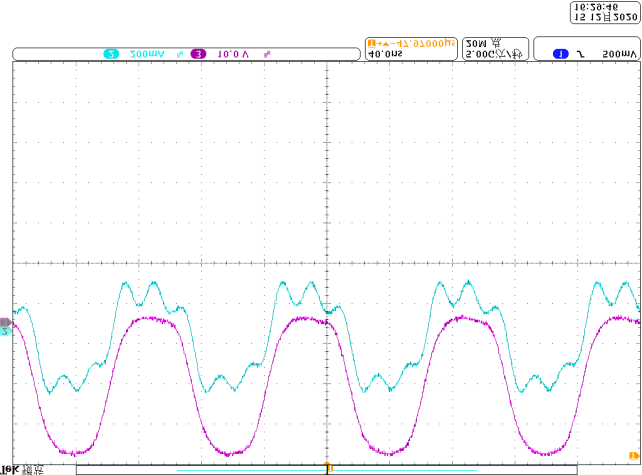
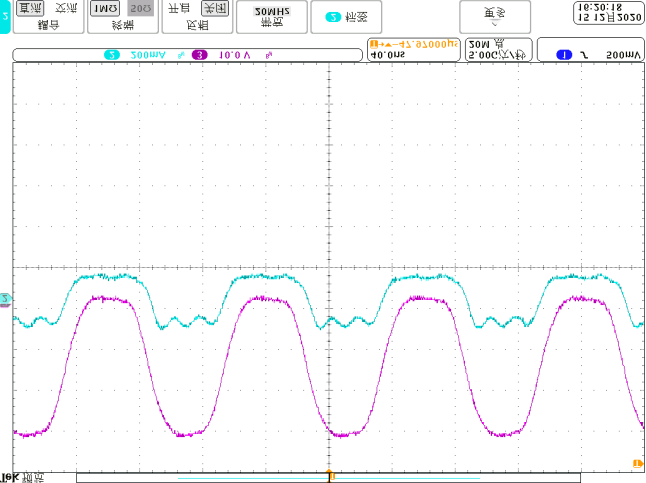
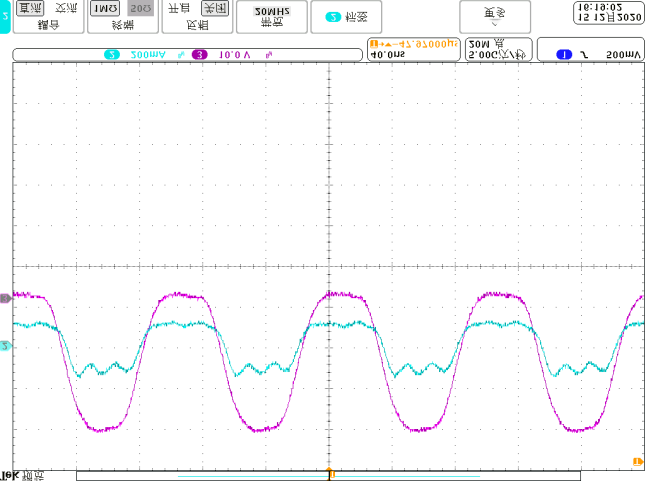
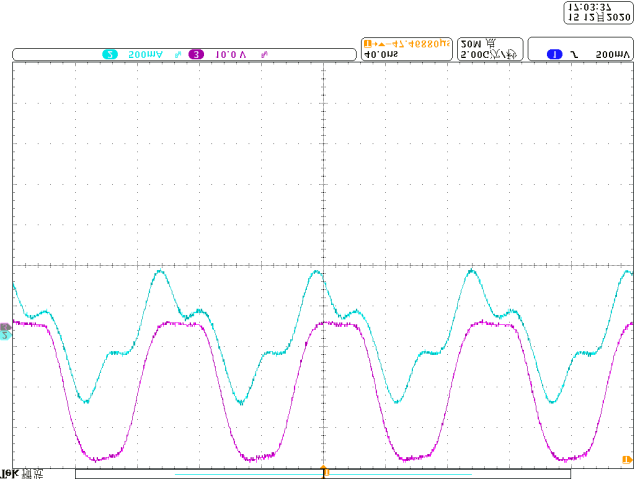
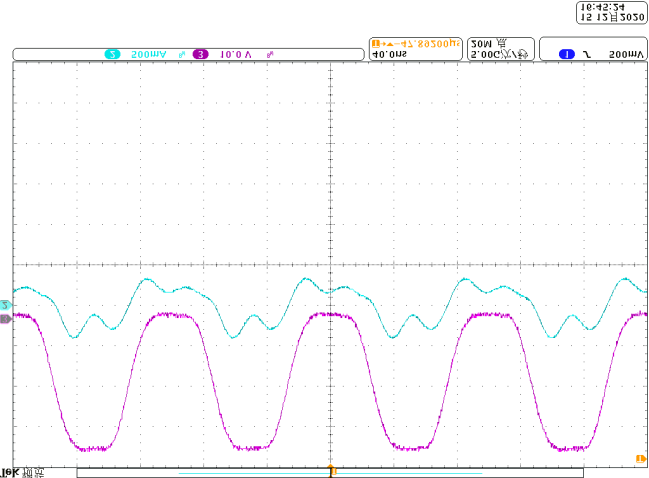
当线圈形状发生变化时，也可以基于所提出的方法进行分析：首先推导空间坐标，然后通过积分运算求出自感和互感，最后也能求解电感值。根据图3中可弯曲线圈的计算结果，已使用不同的线圈进行了实验，相关波形如图18‐图21所示。可以看出，在0度和180度弯曲角度下，阻抗角保持不变。

此外，该拓扑结构的设计也可应用于任何可弯曲空心电感。在其他拓扑结构下，通过代入不同的目标函数，也可针对电感变化的情况进行拓扑设计。

五、结论

本文提出了一种用于10MHz可弯曲直流/直流转换器的平面空心线圈T型匹配网络的优化设计方法。文中分析了可弯曲平面圆形线圈的数学计算方法，并验证了电感计算的精度。针对可变电感效应，对T型匹配网络进行了优化设计，以保持期望的输入阻抗特性。制作了10MHz, 9V/6.3W、输入电压为32V的原型，验证了所提出设计方法的可行性，该原型在弯曲情况下具有更高效率。