矩阵法求解线性回归

 

由于梯度下降算法需要多次迭代，并且需要指定下降速率，如果下降速度过快则可能错过最优点，如果过慢则需要迭代多次，因此还可选用矩阵法求解。

首先给出一些基本数学知识：

矩阵的迹trace为矩阵主对角线元素之和：

　　

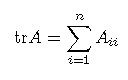
tr(a)=a ,如果a为实数

以下是关于矩阵迹的一些性质：

　　

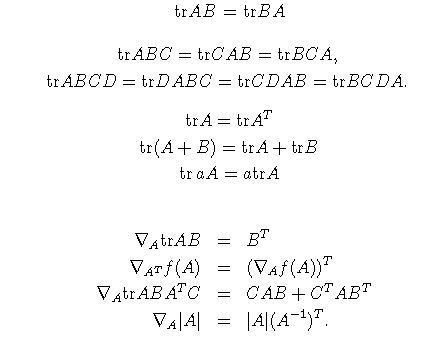
对于多元线性回归，将所有训练数据作为一个矩阵，多元线性回归，也就是多个自变量的线性方程，类似y=a1x1+a2x2+a3x3...：

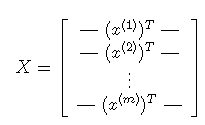
将y值也作为一个矩阵：

 

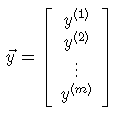
则可得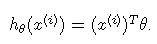

则误差为：

 

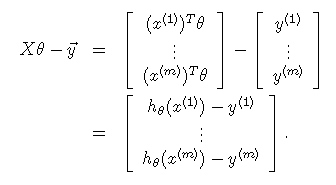
 转变为平方后：

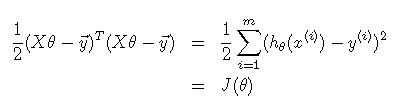
其中转变为平方主要为了统一为正值，前面乘以1/2是方便求导后的计算。

对J(θ)求导，

 

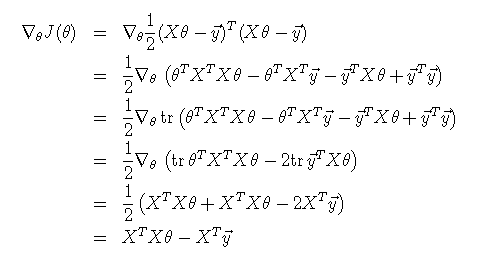
 其中用到上面的求迹公式，以及求导公式，

令上式为0，

 

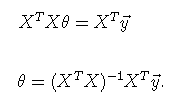
 则可求出最优的系数，矩阵方求解相对简单，不需要多次迭代，但当数据量过大时，即设计矩阵X过大时，对矩阵的乘法即求逆有很大计算复杂度，因此此方法适用于小规模数据。另外，用矩阵法时不需要对输入特征数据中心化。

 

转载于:https://www.cnblogs.com/xqnq2007/p/8073369.html